高三数学第一学期期末独立作业
1．设集合
，则集合
的子集的个数是
A．11 B．10 C．15 D．16
2．已知
A．
B．8 C．18 D． 
3．函数
，则函数
在点
处的变化率是
A．2 B．－2 C．4 D．－4
4．奇函数
满足
，则
A．11 B．－11 C．2 D．－2
5．一班有学员54人，二班有学员42人，现在要用分层抽样的方法从两个班抽出一部分人
参加4×4方队进行军训表演，则一班和二班分别被抽取的人数是
A．9人、7人 B．15人、1人 C．8人、8人 D．12人、4人
6．已知A，B，C是△ABC的三个内角，且
，则角C的大小是
A．
B．
C．
D．
7．
等于 A．－１ B． C．0 D．∞
8．已知函数
，则函数的最大值是
A．
B．
C．
D．
9．函数
的值域是
A．
B．
C．
D．
10．甲乙两人同时从相距72英里的M，N出发且相向而行，甲以每小时4英里的速度步行，
乙第1小时步行2英里，第2小时步行2.5英里，第3小时步行3英里等等（成等差数
列），经过t小时甲乙相遇A点.则一定有 A．
B．
C．
D．以上都不对
11．若
，且
，设
，
,
,则
与
的大小关系是
A．
B．
C．
D．
12.若“p且q”与“p或q”均为假命题,则
A.命题“非p”与“非q”的真值不同 B.命题“非p”与“非q”至少有一个是假命题
C.命题“非p”与“q”的真值相同 D.命题“非p”与“非q”都是真命题
13．将一抛物线F按
=（－1，3）平移后，得到抛物线F`的函数解析式为y=2（x+1）2+3，则F的解析式为
14．设
，
，
，
，则
15．已知
，
过点
，且它们的方向向量
，
满足
，则的方程是
16．某工厂2003年生产某种产品
万件，计划从2004年开始，每年的产量比上一年增长
，经过
年，这家工厂生产这种产品的年产量超过
万件。
17．关于函数
，有下列命题：
①
的图象可由函数
的图象向左平移个单位得到.
②的图象可由函数的图象向左平移个单位得到.
③的图象关于点
对称.
④的表达式可改写成
.
其中正确命题的序号是 .
18．对于每个正整数n，抛物线
与x轴交于An，Bn两点，以
表示该两点的距离，则
=
.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
学号： 姓名： 分数：
13 ；14 ；15 ； 16 ； 17 ； 18 。
19．已知集合
，集合
.
（1）若A的区间长度为3，试求t的值.
（2）某个函数的值域是B，且∈A的概率不小于0.6，试确定t的取值范围.
20．设
有唯一解，
（1）问数列
是否是等差数列？ （2）求
的值.
21．已知
，
，求
的值。
22．平面向量
，点M为直线OP上的一个动点.
（1）当
取最小值，求
的坐标；
（2）当点M满足（1）的条件和结论时，求
的余弦值.
23．某学校为了教职工的住房问题，计划征用一块土地盖一幢总建筑面积为A(m2)的宿舍楼.已知土地的征用费为2388元/m2，且每层的建筑面积相同，土地的征用面积为第一层的2.5倍.经工程技术人员核算，第一、二层的建筑费用相同都为445元/m2，以后每增高一层，其建筑费用就增加30元/m2.试设计这幢宿舍楼的楼高层数，使总费用最少，并求出其最少费用.（总费用为建筑费用和征地费用之和）
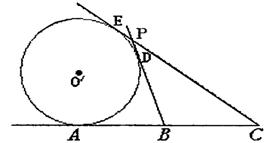
24．已知A、B、C是直线
上的三点，且AB=BC=6，⊙O′切直线于点A，又过B、C
|
的两切线，切点分别为D、E，设两切线交于点P，（1）求点P的轨迹方程；（2）经过点C的直线与点P的轨迹交于M、N两点，且点C分
所成比等于2∶3，求直线的方程.
一、选择题
DDCBA DBDAB AC
二、填空题
13． 14．
15． 16．15 17. ②③④
18. 1
18．略解：因为
，所以，
三、解答题
19．（1）
（2）
.
即
20．（1）由
，所以由题知
.
又因为
. 所以数列是首项为1002，公差等于
的等差数列.
（2）由（1）知
21．解：由得
，又
即
，
，原式=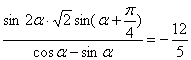
22．解：（1）
点M在OP上，故
共线，又
，
即x=2y
，
，
于是
，
即当且仅当
时，取得最小值－8，此时
（2）当时，有
，
.
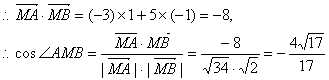23．设楼高为n层，总费用为y元，则征地面积为
，征地费用为
元，楼层建筑费用为[445+445+（445+30）+（445+30×2）+…+445+30×（n－2）]·
元，故
（元）仅当
即n=20（层）时，总费用最少为1000A元…………12分
24．（1）
点轨迹是B，C为焦点，长轴长等于18的椭圆.
以B，C两点所在直线为x轴，线段BC的垂直平分线为y轴建立直角坐标系.
则可设椭圆的方程是
点的轨迹方程
（2）设
，
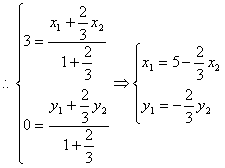
①
又
② 由①、②消去
解得
由C、N可得直线的方程是
