高三数学第一学期期末练习
高三数学(文)
第I卷(选择题 共50分)
一. 选择题:本大题共10个小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 已知椭圆的两个焦点是![]() ,且点
,且点![]() 在椭圆上,则椭圆的标准方程是( )
在椭圆上,则椭圆的标准方程是( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
2. 设集合![]() ,
,![]() ,则
,则![]() 等于( )
等于( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
3. 若![]() ,则
,则![]() 的最大值是( )
的最大值是( )
A. 3 B. 5 C. 7 D. 9
4. 三个数![]() 的大小关系是( )
的大小关系是( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
5. 方程![]() 的实数解的个数是( )
的实数解的个数是( )
A. 0 B. 1 C. 2 D. 3
6. 长方体从同一顶点出发的三条侧棱之和为11,对角线长为![]() ,那么( )
,那么( )
A. 它的全面积为38 B. 它的全面积为76
C. 它的全面积不确定 D. 这样的长方体不存在
7. 5名班委进行分工,其中A不适合做班长,B只适合作学习委员,则不同的分工方案种数为( )
A. 18 B. 24 C. 60 D. 48
8. 已知直线l,m,平面![]() 和
和![]() ,且
,且![]() ,给出下列三个命题
,给出下列三个命题
①若![]() ,则
,则![]() ;②若
;②若![]() ,则
,则![]() ;③若
;③若![]() ,则
,则![]() 。其中正确命题的个数是( )
。其中正确命题的个数是( )
A. 0个 B. 1个 C. 2个 D. 3个
9. 如图,在正方体![]() 中,二面角
中,二面角![]() 的余弦值是( )
的余弦值是( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
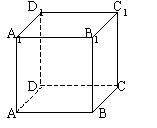
10. 定义在R上的函数![]() 的图像如图所示,它在定义域上是减函数,给出如下命题:
的图像如图所示,它在定义域上是减函数,给出如下命题:
①![]() ;②
;②![]() ;③若
;③若![]() ,则
,则![]() ;④若
;④若![]() ,则
,则![]() 。其中正确的命题是( )
。其中正确的命题是( )
A. ②③ B. ①④ C. ②④ D. ①③
第II卷(非选择题 共100分)
二. 填空题:本大题共4个小题,每小题4分,共16分。把答案填在题中横线上。
11. 直线![]() 与直线
与直线![]() 平行,则实数
平行,则实数![]() 的值为_____________。
的值为_____________。
12. 以抛物线![]() 的焦点为圆心,通径长为半径的圆的方程是_____________。
的焦点为圆心,通径长为半径的圆的方程是_____________。
13. 弹簧上挂的小球作上下振动,它在时间t(秒)时离开平衡位置的距离S(厘米)由下式决定:![]() 。①小球开始时在平衡位置上方
。①小球开始时在平衡位置上方![]() 厘米处;②小球下降到最低点时离开平衡位置向下2厘米处;③经过
厘米处;②小球下降到最低点时离开平衡位置向下2厘米处;③经过![]() 秒小球重复振动一次。以上三种说法正确的是________________________(把你认为说法正确的序号都填上)。
秒小球重复振动一次。以上三种说法正确的是________________________(把你认为说法正确的序号都填上)。
14. 等差数列![]() 中,
中,![]() ,公差
,公差![]() ,则
,则![]()
![]() 的值等于___________________。
的值等于___________________。
三. 解答题:本大题共6个小题,共84分。解答应写出文字说明,证明过程或演算步骤。
15. (本小题满分13分)
已知函数![]() ,且
,且![]() ,
,![]() ,求使
,求使![]() 的x的集合。
的x的集合。
16. (本小题满分13分)
已知函数![]() ,又
,又![]() 成等比数列。
成等比数列。
(I)求函数![]() 的解析式;
的解析式;
(II)设![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() 。
。
17. (本小题满分15分)
已知函数![]() 。
。
(I)求函数![]() 和
和![]() 的定义域;
的定义域;
(II)函数![]() 和
和![]() 是否具有奇偶性,并说明理由;
是否具有奇偶性,并说明理由;
(III)证明函数![]() 在
在![]() 上为增函数。
上为增函数。
18. (本小题满分15分)
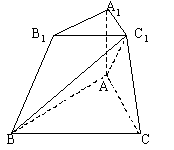
如图,在三棱台![]() 中,侧棱
中,侧棱![]() 底面ABC,
底面ABC,![]() ,
,![]() 。
。
(I)求证![]() 平面
平面![]() ;
;
(II)求证![]() 平面
平面![]() ;
;
(III)求![]() 与
与![]() 所成的角。
所成的角。
19. (本小题满分14分)
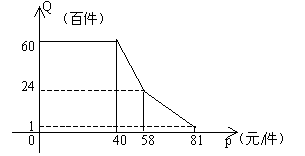
某种消费品专卖店,已知该种消费品的进价为每件40元;该店每月销售量q(百件)与销售价p(元/件)的关系用下图中一条折线表示;职工每人每月工资为600元,该店应交付的其他费用为每月13200元。
(I)试求该店每月销售量q(百件)与销售价p(元/件)的关系;
(II)若该店只安排40名职工,求每月的利润S的最大值?并指出此时该种消费品的销售价是多少。
20. (本小题满分14分)
曲线C是中心在原点,焦点为(2,0)的双曲线的右支,已知它的一条渐近线方程是![]() 。线段PQ是过曲线C右焦点F的一条弦,R是弦PQ的中点。
。线段PQ是过曲线C右焦点F的一条弦,R是弦PQ的中点。
(I)求曲线C的方程;
(II)当点P在曲线C上运动时,求点R到y轴距离的最小值。
【试题答案】
一. 选择题:本大题共10个小题,每小题5分,共50分。
1. A 2. C 3. C 4. B 5. D 6. B 7. A 8. B 9. D 10. B
二. 填空题:本大题共4小题,每小题4分,共16分。
11. ![]() 12.
12. ![]() 13. ①②③ 14. 4008
13. ①②③ 14. 4008
三. 解答题:本大题共6个小题,共84分。
15. (本小题满分13分)
已知函数![]() ,且
,且![]() ,
,![]() ,求使
,求使![]() 的x的集合。
的x的集合。
解:由题意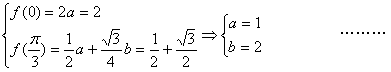 4分
4分
![]() ……9分
……9分
又![]() ,即
,即![]()
![]() ………12分
………12分
所求使![]() 的x的集合为
的x的集合为![]() …………………13分
…………………13分
16. (本小题满分13分)
已知函数![]() ,又
,又![]() 成等比数列。
成等比数列。
(I)求函数![]() 的解析式;
的解析式;
(II)设![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() 。
。
解:(I)函数![]() 的解析式是
的解析式是![]() ………………6分
………………6分
(II)![]() ………………8分
………………8分
![]() ……13分
……13分
17. (本小题满分15分)
已知函数![]() 。
。
(I)求函数![]() 和
和![]() 的定义域;
的定义域;
(II)函数![]() 和
和![]() 是否具有奇偶性,并说明理由;
是否具有奇偶性,并说明理由;
(III)证明函数![]() 在
在![]() 上为增函数。
上为增函数。
解:(I)![]()
![]() 又
又![]()
函数![]() 的定义域为
的定义域为![]()
函数![]() 的定义域
的定义域![]() ……………5分
……………5分
(II)由![]() 的定义域为
的定义域为![]() 可知函数
可知函数![]() 为非奇非偶函数
为非奇非偶函数
![]()
![]() 为偶函数 ……………10分
为偶函数 ……………10分
(III)设![]() 且
且![]()
![]()
![]() 且
且![]() ,
,![]()
所以![]() ,
,![]() ,
,![]()
根据函数单调性的定义知 函数![]() 在
在![]() 上为增函数 …………15分
上为增函数 …………15分
18. (本小题满分15分)
如图,在三棱台![]() 中,侧棱
中,侧棱![]() 底面ABC,
底面ABC,![]() ,
,![]() 。
。
(I)求证![]() 平面
平面![]() ;
;
(II)求证![]() 平面
平面![]() ;
;
(III)求![]() 与
与![]() 所成的角。
所成的角。
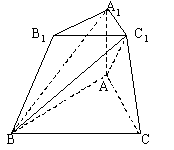
解:![]() 侧棱
侧棱![]() 平面ABC
平面ABC
![]()
又![]()
从而![]() 平面
平面![]() …………4分
…………4分
![]() 平面
平面![]()
![]()
又![]()
![]() 平面
平面![]() ………………8分
………………8分
连接![]() ,
,![]()
![]() 与
与![]() 所成的角是
所成的角是![]() (或它的补角)
(或它的补角)
![]()
![]() 平面
平面![]()
![]() 平面
平面![]()
![]()
在直角三角形![]() 中,
中,![]()
![]() 即 异面直线AC与
即 异面直线AC与![]() 所成的角为
所成的角为![]() ………………15分
………………15分
19. (本小题满分14分)
某种消费品专卖店,已知该种消费品的进价为每件40元;该店每月销售量q(百件)与销售价p(元/件)的关系用下图中一条折线表示;职工每人每月工资为600元,该店应交付的其他费用为每月13200元。
(I)试求该店每月销售量q(百件)与销售价p(元/件)的关系;
(II)若该店只安排40名职工,求每月的利润S的最大值?并指出此时该种消费品的销售价是多少。
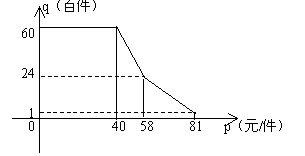
解:(I)由图可得![]() …………6分
…………6分
(II)由题意
![]() …………10分
…………10分
当![]() 时,求得
时,求得![]() 时,
时,![]()
当![]() 时,求得
时,求得![]() 时,
时,![]() ……………15分
……………15分
所以当该店只安排40名职工,每月的利润的最大值为7800元,此时该种消费品的销售价是55元。
20. (本小题满分14分)
曲线C是中心在原点,焦点为(2,0)的双曲线的右支,已知它的一条渐近线方程是![]() 。线段PQ是过曲线C右焦点F的一条弦,R是弦PQ的中点。
。线段PQ是过曲线C右焦点F的一条弦,R是弦PQ的中点。
(I)求曲线C的方程;
(II)当点P在曲线C上运动时,求点R到y轴距离的最小值。
解:(I)设曲线C的方程为![]()
![]() 解得
解得![]()
故所求曲线C的方程是![]() ……………5分
……………5分
(II)当弦PQ的斜率存在时,则弦PQ的方程为![]()
代入 曲线C的方程得![]()
设点![]()
由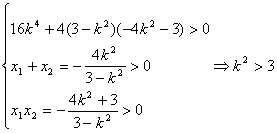 ………………9分
………………9分
点R到y轴距离![]() ………………12分
………………12分
当弦PQ的斜率不存在时,点R到y轴距离![]() ………………13分
………………13分
点R到y轴距离的最小值为2 ………………14分