高三数学调研考试
说明：本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共150分.考试时间120分钟.
参考公式：
sinα+sinβ=2sin
sinα-sinβ=2cos
cosα+cosβ=2cos
cosα－cosβ=-2sin
第Ⅰ卷 (选择题 共60分)
一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）
1.下面四个函数中，不存在反函数的函数的是
A.ｙ=-
B.ｙ=x4
C.ｙ=3x
D.ｙ=
2.设α、β为钝角且sinα=
,cosβ=-
,则α+β的值为
A.
B. 
C.
D.
或
3.对于直线a、b和平面α、β，a∥b的一个充分条件是
A.a∥α,b∥α B.a∥α,b∥β,α∥β
C.a⊥α,b⊥β,α∥β D.α⊥β,a⊥α,b∥β
4.函数f(x)=ctgwx(w＞0)图象的相邻两支截ｙ=
所得线段长为
.则f()的值是
A.0
B.-1
C.1
D.
5.今有一组实验数据如下
t 1.993 3.002 4.001 5.032 6.121
S 1.501 4.413 7.498 12.04 17.93
现准备下列函数中的一个近似地表示数据满足的规律，其中接近的一个是
A.S-1=2t-3
B.S=
C.2S=t2-1 D.S=-2t-2
6.已知A（0，0），B（a，b），P1是AB中点，P2是BP1中点，P3是P1P2中点，…，Pn+2是PnPn+1中点，则Pn点的极限位置
A.
B.
C.
D.
7.函数f(x)=x2+
(x≤-
)的值域是
A.
B. 
C.
D. 
8.已知a≠b,m=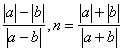
,则m、n之间的关系是
A.m＞n B.m＜n C.m=n D.m≤n
9.如图在正三棱锥A—BCD中，E、F分别是AB、BC的中点，EF⊥DE,且BC=1，则正三棱锥
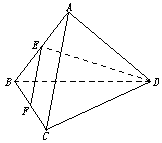A—BCD的体积是
A.
B. 
C. 
D.
10.在平面直角坐标系中，x轴正半轴上有5个点，ｙ轴正半轴有3个点，将x轴上这5个点和ｙ轴上这3个点连成15条线段，这15条线段在第一象限内的交点最多有
A.30个 B.35个 C.20个 D.15个
11.若直线ｙ=kx+1与曲线x=
有两个不同的交点，则k的取值范围是
A.-
B.-
＜k＜-1
C.1＜k＜
D.k＜或k＞
12.某厂有一批长为2.5 m的条形钢材，要截成60 cm长的A型和43 cm长的B型的两种规格的零件毛坯，则下列哪种方案最佳（所剩材料最少）
A.A型4个 B.A型2个，B型3个
C.A型1个，B型4个 D.B型5个
第Ⅱ卷 (非选择题 共90分)
二、填空题（本大题共4小题，每小题4分，共16分.把答案填在题中横线上）
13.椭圆
(a＞b＞0)的离心率为，F为左焦点，A为左顶点，B为上顶点，C为下顶点，直线CF与AB交于D，则tgBDC=__________.
14.已知（x+1）6·(ax-1)2的展开式中，x3的系数是56，则实数a的值为______________.
15.（理）已知直线l的参数方程为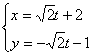
(t为参数)，若以原点为极点，x轴的正半轴为极轴的极坐标系中，点P的极坐标为（-2，π），则点P到直线l的距离为______________.
（文）函数ｙ=sinx-sinx的最小值为______________.
16.在△ABC中A＞B，下列不等式中正确的是
①sinA＞sinB;②cosA＜cosB;③sin2A＞sin2B;④cos2A＜cos2B
其中正确的序号为______________.
三、解答题（本大题共6个小题，共74分.解答应写出文字说明、证明过程或演算步骤）
17.（本小题满分12分）
已知集合A={x
＜1＝,B={xlog4(x+a)＜1＝,若A∩B=
，求实数a的取值范围.
18.（本小题满分12分）
已知复数z满足(z+1)(
+1)=z2,且
是纯虚数;
(Ⅰ)求z;
(Ⅱ)求argz.
19.（本小题满分12分）
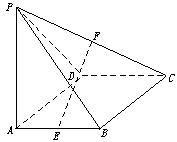
在四棱锥P—ABCD中，底面ABCD是矩形，侧棱PA垂直于底面，E、F分别是AB、PC的中点，
（Ⅰ）求证：CD⊥PD；
（Ⅱ）求证：EF∥平面PAD；
（Ⅲ）当平面PCD与平面ABCD成多大角时，直线EF⊥平面PCD.
20.（本小题满分13分）
已知抛物线C：ｙ=-x2+6,点P（2，4），A、B在抛物线上，且直线PA、PB的倾斜角互补；
（Ⅰ）证明：直线AB的斜率为定值；
（Ⅱ）当直线AB在ｙ轴上的截距为正数时，求△PAB的面积S的最大值及此时直线AB的方程.
21.（本小题满分12分）
（理）在东西方向直线延伸的湖岸上有一港口A，一艘机艇以40 km/h的速度从A港出发，30分钟后因故障而停在湖里，已知机艇出发后，先按直线前进，以后又改成正北，但不知
最初的方向和何时改变的方向，如果去营救，用图示表示营救区域（提示：满足不等式ｙ≥ax+b的点（x,ｙ）不在ｙ=ax+b的下方）.
（文）国贸城有一个个体户，2001年一月初向银行贷款10万元作开店资金，每月底获得的利润是该月初投入资金的20%，每月底所缴的房租和所得税为该月所得金额（含利润）的10%，每月生活费和其他开支为3000元，余款作为资金全部投入再营业，如此继续，问到2001年年底，这一个体户有现款多少元？（1.0812≈2.5）
22.（本小题满分13分）
（理）若{an}是正项递增的等差数列，n∈N,k≥2,k∈N,求证：
（Ⅰ）
;
(Ⅱ)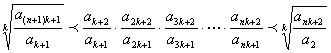
;
（文）已知等比数列{xn}的各项为不等于1的正数，数列{ｙn}满足ｙn·logxna=2(a＞0且
a≠1)，设ｙ3=18,ｙ6=12.
(Ⅰ)求数列{ｙn}的前多少项和最大，最大值为多少？
（Ⅱ）试判断是否存在自然数M，使当n＞M时，xn＞1恒成立？若存在，求出相应的M，若不存在，请说明理由；
（Ⅲ）令an=logxnxn+1(n＞13,n∈N),试判断数列{an}的增减性？
高三数学调研考试答案
一、1.B 2.C 3.C 4.A 5.C 6.C 7.C 8.D 9.B 10.A 11.B 12.B
二、13.-3
14. -1或6 15.(理)
(文)-2 16.①②④
三、17.解：由(
＜1得x2-x-6＞0，解得x＞3或x＜-2
A={xx＞3或x＜-2
4分
由log4(x+a)＜1得0＜x+a＜4
∴B={x-a＜x＜4-a
8分
∵A∩B=,∴
10分
∴1≤a≤2 即a的取值范围是：{a1≤a≤2} 12分
18.解：(Ⅰ)(z+1)(
+1)=z2,∴
+1=z2
∵
=z2 ∴z++1=0 3分
设z=x+ｙi(x,ｙk∈R),则=x-ｙi
∴x=-,z=-+ｙi 5分
又∵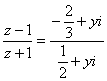
且是纯虚数
∴ｙ2-
=0且ｙ≠0 7分
∴ｙ=±
∴z=-±i 10分
(Ⅱ)当z=-+i时，argz=
11分
当z=--i时，argz=
12分
19.(Ⅰ)证明：∵ABCD是矩形∴CD⊥AD
又∵PA⊥平面ABCD，AD是PD在平面ABCD上的射影
由三垂线定理：CD⊥PD 3分
(Ⅱ)证明：取CD中点N，连结EN、FN
∵E、F分别是AB、PC的中点
∴FN∥PD,EN∥AD.
∵FN
平面PAD，EN平面PAD
∴FN∥平面PAD，EN∥平面PAD 5分
∵FN∩EN=N
∴平面EFN∥平面PAD
∵EF
平面EFN，
∴EF∥平面PAD 7分
(Ⅲ)解：当平面PCD与平面ABCD成45°角时，直线EF⊥平面PCD 8分
∵AB∥CD
∴CD⊥AD,PD⊥CD,即∠PDA就是侧面PCD与底面ABCD所成二面角的平面角.
连结PE，EC
又∠PDA=45°∴PA=AD=BC,
又AE=EB ∴Rt△PAE≌Rt△CBE ∴PE=EC 10分
∵F为PC的中点 ∴EF⊥PC，又FN∥PD,EN∥AD
∴CD⊥FN, ∴CD⊥EN
∴CD⊥平面EFN ∴CD⊥EF
∵CD∩PC=C，
∴EF⊥平面PCD 12分
20.解：(Ⅰ)易知点P在抛物线C上，设PA的斜率为k
则直线PA的方程是ｙ-4=k(x-2) 1分
代入ｙ=-x2+6中，整理得：x2+2kx-4(k+1)=0
此时方程应有根xA及2，由韦达定理得：
2xA=-4(k+1) ∴xA=-2(k+1)
∴ｙA=k(xA-2)+4=-2k2-4k+4 4分
∴A(-2(k+1),-2k2-4k+4)
由于PA与PB的倾斜角互补，故PB方程的斜率为-k.
同理可得：B(-2(-k+1),-2k2+4k+4) ∴kAB=2 6分
(Ⅱ)由（Ⅰ）得∴直线AB的方程为：ｙ=2x+b,b＞0，
代入方程ｙ=-x2+6消去ｙ得：x2+2x+b-6=0
AB=2
9分
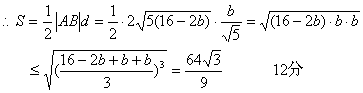
此时方程为：ｙ=2x+
13分
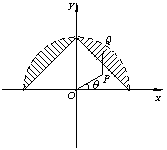21.(理)解：建立如图所示的直角坐标系，设机艇先沿OP方向前进m到P处，然后向北前进n到达Q，设∠XOP=θ，Q(x,ｙ)2分
可知
4分
∴AQ2=x2+ｙ2=m2+n2+2mnsinθ≤(m+n)2=400
∵机艇中途左拐
∴x2+ｙ2＜400 7分
又∵x+ｙ=m(sinθ+cosθ)+n=
·m+n≥m+n=20
即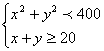
10分
根据题中的提示及对称性，结合上述不等式组，可得营救区域为上图所示阴影区域，但不包括圆周上的点. 12分
(文)解：设第n月月底所得现款an万元，
依题意an+1=an(1+20%)-an(1+20%)10%-0.3=1.08an-0.3 4分
化为an+1-
=1.08(an-)
则{an-}为等比数列，其中a1=1.08×10-0.3=(10-)×1.08+ 8分
∴an-=(10-)1.08n
即an=(10-)1.08n+ 10分
∴a12=(10-
)·1.0812+
代入1.0812≈2.5,得a12=19.375 12分
答：到这一年年底，个体户有现款193750元.
22.解：(Ⅰ)∵ak+1=ak+1+d,ak=ak+1-d
∴ak+2·ak=
又∵ak+1＞0,ak+2＞0,ak＞0
∴ 4分
(Ⅱ)利用(Ⅰ)的结论可得
6分
令A=
，从而有
Ak＞
9分
又Ak=
从而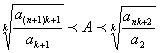
13分
(文)(Ⅰ)ｙn=2logaxn，
设{xn}的公比为q(q≠1)
∵ｙn+1-ｙn=2(logaxn+1-logaxn)=2loga
=2logaq
∴{ｙn}为等差数列，设公差为d 2分
∵ｙ3=18,ｙ6=12,
∴d=-2,
∴ｙn=ｙ3+(n-3)(-2)=24-2n
设前k项为最大，则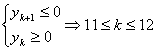
4分
∴前11项和前12项和为最大，其和为1325分
(Ⅱ)xn=a12-n,n∈N*
若xn＞1，则a12-n＞1
当a＞1时，n＜12，显然不成立 7分
当0＜a＜1时，n＞12，
∴存在M=12，13，14，…，
当n＞M时，xn＞1 9分
(Ⅲ)an=
10分
∵
12分
∴an+1＜an
∴n＞13时数列{an}为递减数列 13分