高三数学冲刺练习（18）

高三数学冲刺练习（18）

1.直线与平面α内共点的三条直线a、b、c分别成等角那么与平面α所成的角为

A．　　　　  B．　　　　  C．　　　 D．

联想：（1）三条两两异面直线，且两两成角相等，这三条直线与平面α都平行，则它们所成的角为　　　　　　  。

(2)　两条异面直线a、b所成的角为，过空间一定点P的直线有且仅有三条与a、b所成的角为75⁰，则a与b所成的角为　　　　　　　 。

题号	1	（1）	（2）
答案

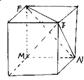
2.如图，E，F，M，N是正方体的四个顶点，记d₁为F到面FMN的距离，d₂为E面EMN的距离，d₃为M到面EFN的距离，那么d₁,d₂,d₃的大小关系为　　A．d₁＜d₂＜d₃ B．d₂＜d₃＜d₁ C．d₂＜d₁＜d₃D．d₃＜d₂＜d₁

联想：（1）三棱柱ABC—A₁B₁C₁的体积为V，P、Q分别为AA₁、CC₁上的点，而且满足PA=QC₁，则V_B－APQC=　　A.　　　　  B.　　　 C.　　　 D.

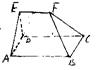（2）如图，多面体ABCDFE中，ABCD是边长为3的正方形，EF∥平面ABCD，EF=，EF到面ABCD的距离为2，则多面体的体积为　

 A．　　　　B．5　　　 C．6　　　　D．

题号	2	（1）	（2）
答案

3．光线从点P（2，3）射到直线y=－x－1上，反射后经点 Q（1，1），则反射光线方程为　A．x－y+1=0　　 B．4x－5y+31=0　 C．4x－5y+16=0　 D．4x－5y+1=0

联想（1）光线x－2y+5=0遇到直线3x－2y+7=0即行反射，光线与反射光线所夹角是

A．2arctan　　B．　　  C．2 arctan　　  D．

(2)光线从点P（1，3）入射到y轴后即行反射，射到x轴上再即行反射，最后一次的反射光线经过点Q（5，2），则第一次反射光线方程　　　　　　　 。

题号	3	（1）	（2）
答案

4．若x[0,3]时，不等式a≥x²－2x－1恒成立，则实数a的最小值是

A．－2　　　　　 B．2　　　　　 C．－1　　　　　  D．不存在

联想：若ax+2≥20x－x²在（0，+）恒成立，则实数a的取值范围是　　　　　　　 。

题号	4	（1）
答案

5．在等差数｛a_n｝中，a₁+a₃=4，a₄+a₆= －2，如果a_n=log₃b_n，则 ()=　　　　　　　  。

　联想：等差数列｛｝中，a₁－a₄+a₆+a₁₀－a₁₂+a₁₅=2，则前15项的和为S₁₅=

A．－15　　　　　  B．15　　　　　  C．－30　　　　　  D．30

题号	5	（1）
答案

6．正方体的8个顶点中， 任何两点的连线中有　　  对异面直线。

　联想：（1）某市要组成一支有12名运动员的篮球队，这些队员要从7所不同的学校选出，每校至少一人，则有　　　　 种不同的选派方案。

（2）某仪表显示屏上排有七个小孔，每个小孔可显示出0或1，若每次显示其中三个孔，但相邻两个孔不能同时显示，则这个显示屏可以显示的不同信号的种数是　　　 。

题号	6	（1）	（2）
答案

7．椭圆的一个焦点为圆心，焦距为半径的圆过椭圆的两个顶点，则此椭圆的离心率e=　　　 。

　联想：（1）双曲线中，左焦点为F，右顶点为A，虚轴顶点为B，

若BF⊥AB，则离心率e=　　　　 。

（2）椭圆（a＞b＞0）的两个顶点A（a,0）,B(0,b)，若右焦点F到直线AB的距离为，则离心率e=　　　 。

题号	7	（1）	（2）
答案

8．某纯净水制造厂在净化水过程中，每增加一次过滤可减少水中杂质20%，要使水中杂质减少到原来的5%以下，则至少需过滤的次数为

　　A．5　　　　　 B．10　　　　　　 C．14　　　　　  D．15

　联想：某公司一月份推出新产品A，成本为400元/件，经试销调查，销售量与销售价的关系如下表：

销售价（x元/件）	650	662	719	800	900
销售量（y件）	350	338	281	200	100

据此，写出x与y可满足的一个函数关系式　　　　　　　　 ；

并据此，应将销售价定为　　　　 元时，利润最大。

题号	8
答案