高三数学测试题(1)
一、填空题(每小题4分,本题满分48分)
1.复数![]() 是纯虚数,则
是纯虚数,则![]() =
.
=
.
2. 设![]() ,且
,且![]() ,则
,则![]() =
.
=
.
3.已知正![]() 的边长为
的边长为![]() ,则到三个顶点的距离都为1的平面有_________个.
,则到三个顶点的距离都为1的平面有_________个.
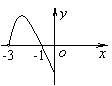 4.已知
4.已知![]() 、
、![]() 是方程
是方程![]() 的两个根,则
的两个根,则![]() _________.
_________.
5.如果![]() 是定义在
是定义在![]() 上的偶函数,且当
上的偶函数,且当![]() 时,
时,
![]() 的图象如图所示,那么不等式
的图象如图所示,那么不等式![]() 的解集为 .
的解集为 .
6.规定记号“![]() ”表示一种运算,即
”表示一种运算,即![]() . 若
. 若![]() ,则函数
,则函数![]() 的值域是___________.
的值域是___________.
7.已知![]() 依次成等比数列,则
依次成等比数列,则![]() 在区间
在区间![]() 内的解集为
.
内的解集为
.
8. 已知数列![]() 中,
中,![]() ,则数列
,则数列![]() 的最大项是第
项.
的最大项是第
项.
9.有一组数据:![]() ,它们的算术平均值为10,若去掉其中最大的
,它们的算术平均值为10,若去掉其中最大的![]() ,余下数据的算术平均值为9;若去掉其中最小的
,余下数据的算术平均值为9;若去掉其中最小的![]() ,余下数据的算术平均值为11. 则
,余下数据的算术平均值为11. 则![]() 关于n的表达式为__________;
关于n的表达式为__________;![]() 关于n的表达式为_______.
关于n的表达式为_______.
10.椭圆![]() 上到两个焦点距离之积最小的点的坐标是________________.
上到两个焦点距离之积最小的点的坐标是________________.
11. 设![]() ,
,![]() 与
与![]() 是
是![]() 的子集,若
的子集,若![]() ,则称
,则称![]() 为一个“理想配集”,那么符合此条件的“理想配集”的个数是 .(规定
为一个“理想配集”,那么符合此条件的“理想配集”的个数是 .(规定![]() 与
与![]() 是两个不同的“理想配集”)
是两个不同的“理想配集”)
12.已知集合![]() 、
、![]() 、
、![]() ,
,![]() ,
,![]() ,
,![]() ,若
,若![]() ,
,![]() ,
,![]() ,下列命题中: ①
,下列命题中: ①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]()
正确命题的序号为__________(注:把你认为正确的序号都填上)
二、选择题(每小题4分,本题满分12分)
13.已知非零向量![]() ,则
,则![]() 是
是![]() 与
与![]() 垂直的( )
垂直的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
14.若![]() ,且
,且![]() ,则m、n、p、q的大小顺序是 ( )
,则m、n、p、q的大小顺序是 ( )
(A)m<p<q<n (B)p<m<q<n (C)m<p<n<q (D)p<m<n<q
15.关于x的方程![]() 有一个根为1,则△ABC中一定有( )
有一个根为1,则△ABC中一定有( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
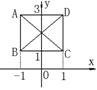 16.函数
16.函数![]() 在区间
在区间![]() 上的值域是
上的值域是![]() ,则点
,则点![]() 的
的
轨迹是图中的线段( )
(A)AB和AD (B)AB和CD
(C)AD和BC (D)AC和BD
三、解答题(本题满分86分)
17.若复数![]() 与
与![]() 在复平面上所对应的点关于
在复平面上所对应的点关于![]() 轴对称,且
轴对称,且![]() ,求
,求![]() .(本题12分)
.(本题12分)
18.三角形ABC中,三个内角A、B、C的对边分别为![]() ,若
,若![]() 且
且![]() ,求角C的大小. (本题14分)
,求角C的大小. (本题14分)
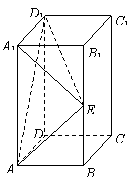 19.长方体
19.长方体![]() 中,
中,![]() ,
,![]() ,
,![]() 是侧棱
是侧棱![]() 的中点.
的中点.
(1)求证:直线![]() 平面
平面![]() ;(本题15分)
;(本题15分)
(2)求三棱锥![]() 的体积;
的体积;
(3)求二面角![]() 的平面角的大小.
的平面角的大小.
20.学校食堂改建一个开水房,计划用电炉或煤炭烧水,但用煤时也要用电鼓风及时排气,用煤烧开水每吨开水费用为![]() 元,用电炉烧开水每吨开水费用为
元,用电炉烧开水每吨开水费用为![]() 元
元
![]() ,
,
![]()
其中![]() 为每吨煤的价格,
为每吨煤的价格,![]() 为每百度电的价格. 如果烧煤时的费用不超过用电炉时的费用,则用煤烧水,否则就用电炉烧水. (本题14分)
为每百度电的价格. 如果烧煤时的费用不超过用电炉时的费用,则用煤烧水,否则就用电炉烧水. (本题14分)
(1)如果两种方法烧水费用相同,试将每吨煤的价格表示为每百度电价的函数;
(2)如果每百度电价不低于60元,则用煤烧时每吨煤的最高价是多少?
21. 已知椭圆![]() (本题15分)
(本题15分)
(1)
若圆![]() 与椭圆相交于A、B两点且线段AB恰为圆的直径,求椭圆方程;
与椭圆相交于A、B两点且线段AB恰为圆的直径,求椭圆方程;
(2) 设L为过椭圆右焦点F的直线,交椭圆于M、N两点,且L的倾斜角为600.
求![]() 的值.
的值.
22.(理科)已知二次函数![]() 的定义域为
的定义域为![]() ,
,
且![]() 的最大值为M. (本题16分)
的最大值为M. (本题16分)
(Ⅰ)试证明![]() ;
;
(Ⅱ)试证明![]() ;
;
(Ⅲ)当![]() 时,试求出
时,试求出![]() 的解析式.
的解析式.
高三数学测试题(1) 参考答案
一、填空题
1.
![]() ; 2. 3;
3.8; 4.
; 2. 3;
3.8; 4.![]() ; 5.
; 5.![]() ; 6.
; 6.![]() ; 7.
; 7.![]()
8. 12、13;
9.![]() ; 10.(±5,0); 11. 9;
12.②
; 10.(±5,0); 11. 9;
12.②
二、选择题
13.C; 14.B; 15.A; 16. B
三、解答题
17.![]() 或
或![]() ,则
,则![]() 或
或![]()
18.由![]() =cosB,故B=600,A+C=1200.
=cosB,故B=600,A+C=1200.
于是sinA=sin(1200-C)=![]() ,又由正弦定理有:
,又由正弦定理有:![]() ,
,
从而可推出sinC=cosC,得C=450.
19.(1)依题意:![]() ,
,![]() ,则
,则![]() 平面
平面![]() .
.
(2)![]()
(3)取![]() 的中点
的中点![]() ,连
,连![]() ,则
,则![]() 、
、![]() ,所以
,所以![]() 平面
平面![]() .过
.过![]() 在平面
在平面![]()
中作![]() ,交
,交![]() 于
于![]() ,连
,连![]() ,则
,则![]() ,所以
,所以![]() 为二面角
为二面角![]() 的平面角.在
的平面角.在![]() 中,
中,![]()
![]()
20.(1)由题意得:![]() ,即
,即![]()
![]() .
.
(2)由S≤P得![]() ∵60 ≤n≤76,∴0≤
∵60 ≤n≤76,∴0≤![]() ≤4
≤4
∴当![]() =1时,
=1时,![]() ,此时n=75. 答:每吨煤的最高价为153元.
,此时n=75. 答:每吨煤的最高价为153元.
21.(1)![]() (2)∴
(2)∴![]() 或
或![]() .
.
22.(Ⅰ)证明:∵![]() ,
, ![]()
![]()
![]()
∴![]()
(Ⅱ)证明:依题意,![]() ,
,![]() ,
, ![]()
又![]() ,
,![]() ,
,![]()
∴![]()
![]()
![]()
∴![]()
(Ⅲ)依![]() 时,
时,![]() ,
,![]() ①
同理
①
同理![]() ②
② ![]() ③
③
②+③得:![]() ④ 由①、④得:
④ 由①、④得:![]() .
.
当![]() 时,分别代入②、③得:
时,分别代入②、③得:![]() ,因此
,因此![]() .
.