高三数学测试题(2)

高三数学测试题(2)

一、填空题

1. 已知集合A={0，2，3}，B={}，则B的子集的个数是　　　　.

2. 若函数的图象关于对称，则=______________.

3．在长方体中,分别是与的中点，则直线与

　 的位置关系是_______; 它们所成角的大小是_______；点到对角线的距离是_______.

4. 在△ABC中，已知，则的值等于　　　 .

5. 不等式的解集为　　　　　　　 .

6．设非零复数x，y满足，则代数式的值是　　　　 .

7．袋内有大小相同的四个白球和三个黑球，从中任意摸出3个球，其中只有一个黑球的概率

　 是　 　　 .

8．一种专门占据内存的计算机病毒，开机时占据内存，然后每3分钟自身复制一次，复制

　 后所占内存是原来的2倍，那么开机后经过　　 分钟，该病毒占据内存.（）

9．已知是两条直线，是两个平面，有下列4个命题：

　 ①若，则;　　　　　  ②若，则

　 ③若则;　　　④若异面， ,则.

　 其中正确命题的序号是　　　　　　  .

10. 对任意两个集合，定义、.

　 设 ， ，则　　 　　　　　　 .

11.在直角坐标系中,横、纵坐标均为整数的点叫格点.若函数的图象恰好经过个格点,

　 则称函数为阶格点函数. 下列函数中为一阶格点函数的序号是　　　　　　  .

（1）； 　 （2）；　　 （3）； 　 （4）.

12．将三种不同的颜色均涂入图中五个区域中，每个区域涂一种颜色，且相邻的区域不能涂同一种颜色，不同的涂色方法共有_________种.（以数字作答）

二、选择题

13. 函数的图象与的图象在区间上(　　 )

(A) 有无交点无法确定　　　　　　　　　　　　 (B) 一定没有交点

(C) 有且只有一个交点　　　　　　　　　　　　 (D) 至少有一个交点

14．若不等式的解集为那么不等式的解集为(　　 )

（A）　（B）　（C）　 (D)

15．设的展开式的各项系数之和为，且二项式系数之和为，，则展开式中项的系数为（　　 ）

（A）　　　 （B）　　　　（C）　　　　（D）

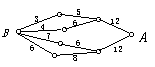16．如图，小圆圈表示网络的结点，结点之间的连线表示它们有网线

相联.连线标注的数字表示该段网线单位时间内可以通过的最大信

息量. 现从结点向结点传递信息，信息可以分开沿不同的路线

同时传递。则单位时间内传递的最大信息量为(　　 )

（A）26　 　　　　　（B）24　　　　　　　 （C）20　 　　　　　　（D）19

三、解答题

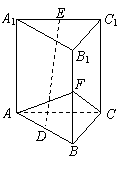17. 如图，正三棱柱中，AB=2，D是AB的中点，E是A₁C₁

的中点，F是B₁B中点，异面直线CF与DE所成的角为90°.

（1）求此三棱柱的高；

（2）求二面角C—AF—B的大小.

18. 某医药研究所开发一种新药，如果成人按规定的剂量服用，据监测：服药后每毫升血液中的含药量y与时间t之间近似满足如图所示的曲线.

（1）写出服药后y与t之间的函数关系式；

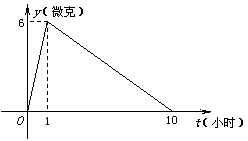（2）据测定：每毫升血液中含药量不少于4微克时治疗疾病有效，假若某病人一天中第一次服药

　　 时间为上午7:00，问一天中怎样安排服药的时间（共4次）效果最佳？

19. 已知函数，数列满足且.

（1）求数列的通项公式；

（2）若数列的通项，的前项之和为，试比较和的大小.

20.设，函数的定义域为，且，当时，，求:

(1) 及的值；

(2)函数的单调递增区间；

(3) 时，，求,并猜测时，的表达式.

高三数学测试题(2) 参考答案

一、填空题

1. 16;　　 2. 6;　　　3. 相交直线，，;　　　4. 1;　　　5. ;　　　6．1;

7．;　　　8．45;　　　9．③④;　　　10. ;　　　11.;　　　12．42.

二、选择题

13. D;　 14. A;　 15. C;　 16. D

三、解答题

17．(1)取的中点分别为，连结，交于点，则点为的中点，因，

则△∽△，因H为BC中点,，则,，∴

则，在Rt△HCC₁，, 解得HC₁=，.

另解：取AC中点O，以OB为x轴，OC为y轴，建立空间坐标系，设棱柱高为h，则C（0，1，0），F（），

　　　  ,，,则CF⊥DE.

(2)连CD, 得CD⊥面AA₁B₁B，作DG⊥AF，连CG，则CG⊥AF，所以∠CGD是二面角的平面角，又在Rt△AFB中，AD=1，BF=1，AF=，从而DG=,∴tg∠CGD=,即∠CGD=.

18．(1)依题得，

(2)设第二次服药时在第一次服药后t₁小时，则,因而第二次服药应在11:00；

　　  设第三次服药在第一次服药后t₂小时，则此时血液中含药量应为两次服药量的和，即有

解得t₂=9小时，故第三次服药应在16:00；

　　  设第四次服药在第一次后t₃小时（t₃>10），则此时第一次服进的药已吸收完，此时血液中含药量应为第二、

三次的和，解得t₃=13.5小时，故第四次服药应在20:30.

19．(1)由,得,

又，

所以是首项，公差为1的等差数列，故即.

(2)由(1)得，

所以，令,

解得：，所以, 当时，；当时， .

20．(1)，

，

，

，

，

.

(2),的增区间为.

　 （3），，所以，

因此是首项为，公比为的等比数列，故，猜测.