高三数学测试题(8)
一、填空题
1．函数
存在反函数的充要条件是
.
2．集合
，
，则
的取值范围是
.
3．已知点
、
，C是圆
上一个动点，则△ABC的面积的最小值为 .
4. 若函数
的定义域为
，则实数a的取值范围是
.
5.
已知O为直二面角
的棱MN上的一点，射线OE，OF分别在
内，并且
，则∠EOF的大小为
.
6. 等差数列
中，
，公差不为零，且
、
、
恰好成等比数列，那么该等比数列
公比的值等于 .
7．过点
的直线
将圆：
分成两段弧，当其中的劣弧最短时，直线的方
程为 .
8．已知椭圆：
（
）的左、右焦点分别为
、
，以为顶点，为焦点
的抛物线经过椭圆短轴的两端点，则
=
.
9.
过抛物线
的焦点作直线与此抛物线交于P，Q两点，那么线段PQ中点的轨迹方程
是 .
10．设、为曲线
：
的焦点，
是曲线
：
与的一个交点，
则
的值为
.
11．在坐标平面内，由不等式组
所确定的平面区域的面积为____________.
12．在直角坐标系中，已知△
三边所在直线的方程分别为
，则
△内部和边上整点（即横、纵坐标均为整数的点）的总数是
.
二、选择题
13.将奇函数
的图象沿x轴的正方向平移2个单位，所得的图象为C，又设图象
与C
关于原点对称，则对应的函数为( )
(A)
(B)
(C)
(D)
14.已知二面角
，直线
，
，且a与l不垂直，b与l不垂直，那么( )
（A）a与b可能垂直，但不可能平行 （B）a与b可能垂直，也可能平行
（C）a与b不可能垂直，但可能平行 （D）a与b不可能垂直，也不可能平行
15．平行六面体
中，
为
与
的交点。若
，
，
,
则下列向量中与
相等的向量是( )
(A) 
(B) 
(C) 
(D) 
16.等差数列
中，
，公差
，前n项和是
，则有( )
(A)
（B）
（C）
（D）
三、解答题
17.已知函数
(1)求
的最小正周期；(2)求的单调递减区间；
(2)函数的图象经过怎样的平移才能使所得图象对应的函数成为奇函数？
18.已知
，又数列{
}(＞0)
中，
，且其前n项和
对
所有大于1的自然数n都有
，求通项公式，并写出推导过程.
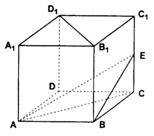
19．在正方体
中，棱长
.
(1)若E为棱
的中点，求证：
；
(2)求二面角C-AE-B的平面角的正切值；
(3)求点
到平面EAB的距离。
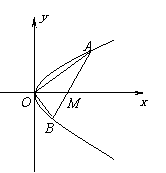20.如图，直线l与抛物线
交于
两点，与x轴相交于点M，且
.
（1）求证：M点的坐标为（1，0）；
（2）求证：OA⊥OB；
（3）求△AOB的面积的最小值.
高三数学测试题(8) 参考答案
一、填空题
1．
; 2．
; 3．
; 4. 
; 5. 60°;
6. 4; 7．
; 8．
; 9. 
; 10．
; 11．16; 12．91;
二、选择题
13. D; 14. B; 15. A; 16. A
三、解答题
17. (1)
; (2)
; (3)右移
个单位.
18. 
.
19．(1)略；（2）3;（3）
20. (1 ) 设M点的坐标为（x0, 0）, 直线l方程为 x = my + x0 , 代入y2 = x得
y2－my－x0 = 0 ① y1、y2是此方程的两根,
∴ x0 ＝－y1y2 ＝1，即M点的坐标为（1, 0）.
(2 ) ∵ y1y2 ＝－1
∴ x1x2 + y1y2 = y12y22 +y1y2 ＝y1y2 (y1y2 +1) = 0
∴ OA⊥OB.
（3）由方程①，y1＋y2 = m , y1y2 ＝－1 , 且 OM = x0 =1,
于是S△AOB = 
OM y1－y2 =
=
≥1，
∴ 当m = 0时，△AOB的面积取最小值1.