高三数学测试题（5）
一、填空题（48分）
1．两两相交的三个平面将空间分成___________个部分。
2．正四棱柱的底面边长为
，高为
，一蚂蚁从顶点
出发，沿正四棱柱的表面爬到顶
点
，那么这只蚂蚁所走过的最短路程为_________。
3．正四棱锥的高与底面边长都是1，侧棱与底面所成的角是
，则
________。
4．在三棱锥的四个面中，直角三角形最多可以有_________个。
5．空间四边形
中，
，
，
分别是
边上的
点，且
为平行四边形，则四边形的周长的取值范围是____________。
6．若
的中点
到平面
的距离为
，点到平面的距离为
，则点
到平面的距
离为_________
。
7．三棱锥
中，侧棱
两两垂直，底面
内一点
到三个侧面的距离分别
是
，那么
________。
8．直三棱柱
中，
，
，
是
上的一点，则到
截面
的距离等于__________。
9．正四面体中，
分别是
的中点，那么
与平面
所成的角的大小为
___________。
10．正三棱锥的底面边长为
，侧棱
，则二面角
的大小是______。
11．设棱长为4的平行六面体
的体积为
，
分别是棱
上的点，且
，则三棱锥
的体积
_______。
12．一个透明密闭的正方体容器中，恰好盛有该容器一半容积的水，任意转动这个正方体，则水
面在容器中的形状可以是：(1)三角形；(2)菱形；(3)矩形；(4)正方形；(5)正六边形。
其中正确的结论是___________________。（把你认为正确的序号都填上）
二、选择题（16分）
13．若平面外的直线与平面所成的角为
，则的取值范围是 （ ）
（A）
（B）
（C）
（D）
14．若正棱锥的底面边长与侧棱长相等，则该棱锥一定不是 （ ）
（A）三棱锥 （B）四棱锥 （C）五棱锥 （D）六棱锥
15．已知三棱锥中，顶点
在底面的射影
是三角形的内心，关于这个三棱锥有
三个命题：①侧棱
；②侧棱
两两垂直；③各侧面与底面所成的二
面角相等。其中错误的是 （ ）
（A）①② （B）①③ （C）②③ （D）①②③
16．若一棱台上、下底面面积分别是
和，它的中截面面积是
，则 （ ）
（A）
（B）
（C）
（D）
三、解答题
17．（6分）在平面几何中有如下特性：从角的顶点出发的一条射线上任意一点到角两边的距离之比
为定值。类比上述性质，请叙述在立体几何中相应地特性，并画出图形。不必证明。
类比性质叙述如下 ：
 |
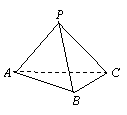18．（8分）三棱锥中，
，其余棱长均为1。
（1）求证：
；
（2）求三棱锥的体积的最大值。
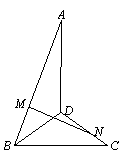19．（10分）直二面角
中，
分别是线段
上的点（不包括端点），
且
,
。
（1）若
与平面所成的角为
，求
的值；
（2）求函数
的解析式及定义域、值域。
20．（12分）直三棱柱中，
，
，分别是棱
、
上的点，且
。
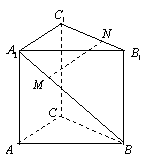（1）求直三棱柱中的高及的长；
（2）动点在
上移动，问在何位置时，
的面积才能取得最小值。
高三数学测试题（5）参考答案
一、填空题
1．6,7,8 2．
3．
4．4个 5．
6．2或14 7．7 8．
9．
10．
11．
12．（2）（3）（4）（5）
二、选择题
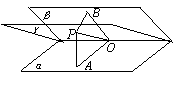13．D 14．D 15．A 16．C
三、解答题
17．立体几何中相应地性质：
（1）从二面角的棱出发的一个半平面内任意一点到二面角的两个面的的距离
之比为定值。
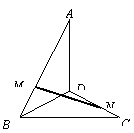（2）从二面角的棱上一点出发的一条射线上任意一点到二面角的两个面的的距离之比为定值。
（3）在空间，从角的顶点出发的一条射线上任意一点到角两边的距离之比为定值。
（4）在空间，射线
上任意一点
到射线
、
、
的距离之比不变。
（5）在空间，射线上任意一点到平面
、
、
的距离之比不变。
（2）——（5）参考给分
18．（1）取
中点
，∵
与
均为正三角形，∴
，
∴
平面
。
（2）当
平面
时，三棱锥的高为
，此时
。
19．（1）作
于
，则
平面
，∴
，
。
，
，由
。
（2）函数解析式
，定义域
，值域
.
20．（1）以
为原点，射线
分别为
轴的正半轴建立空间直角坐标系，
，
。由
得，
，
。
（2）设
，于是，
，
，设
与
所成的角为
，
，
，
则当
时，
。即当与
重合时，
的面积才能取得最小值
。