高三数学测试题(6)
班级____________姓名____________学号____________成绩____________
一、填空题(48分)
1.已知复数![]() 则
则![]() _______。
_______。
2.已知偶函数![]() 的图象与
的图象与![]() 轴有五个公共点,那么方程
轴有五个公共点,那么方程![]() 的所有实根之和为
的所有实根之和为
_______。
3.在![]() 中,
中,![]() ,则
,则![]() _______。
_______。
4.李老师家藏有一套精装的四卷的天龙八部(金庸著),任意排放在书架的同一层上,则卷序自
左向右或自右向左恰为![]() 的概率是__________。
的概率是__________。
5.
已知向量![]() ,其中
,其中![]() ,则满足条件的不共线的向量共有
,则满足条件的不共线的向量共有
_________个。
6. 已知不等式![]() 对
对![]() 取一切负数恒成立,则
取一切负数恒成立,则![]() 的取值范围是 ______________。
的取值范围是 ______________。
7.
一张报纸,其厚度为![]() ,面积为
,面积为![]() ,现将报纸对折(即沿对边中点连线折叠)7次,这时报
,现将报纸对折(即沿对边中点连线折叠)7次,这时报
纸的厚度和面积分别为_________________。
8.
已知矩形![]() 的边
的边![]() 平面
平面![]() 现有以下五个数据:
现有以下五个数据:
![]() 当在
当在![]() 边上存在点
边上存在点![]() ,使
,使![]() 时,则
时,则![]() 可以取_____________。(填上一个正确的数据序号即可)
可以取_____________。(填上一个正确的数据序号即可)
9. 不等式![]() 的解集为
的解集为![]() ,那么
,那么![]() 的值等于___________。
的值等于___________。
10.某人要买房,随着楼层的升高,上下楼耗费的精力增多,因此不满意度升高,当住在第![]() 层楼时,上下楼造成的不满意度为
层楼时,上下楼造成的不满意度为![]() ,但高处空气清新,噪音较小,因此随楼层升高,环境不满意程度降低,设住在第
,但高处空气清新,噪音较小,因此随楼层升高,环境不满意程度降低,设住在第![]() 层楼时,环境不满意程度为
层楼时,环境不满意程度为![]() ,则此人应选________楼。
,则此人应选________楼。
11.在正方体![]() 中选出两条棱和两条面对角线,使这四条线段所在的直线两两都
中选出两条棱和两条面对角线,使这四条线段所在的直线两两都
是异面直线,如果你选定一条面对角线![]() ,那么另外三条线段可以是________________。
,那么另外三条线段可以是________________。
(只需写出一种情况)
12.数列![]() 的第100项是_____________。
的第100项是_____________。
二、选择题(16分)
13.过点![]() 作直线,使其在坐标轴上的截距相等,则满足条件的直线的斜率为( )
作直线,使其在坐标轴上的截距相等,则满足条件的直线的斜率为( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
14.已知平面![]() 与平面
与平面![]() 相交,直线
相交,直线![]() ,则
( )
,则
( )
(A)![]() 内必存在直线与
内必存在直线与![]() 平行,且存在直线与
平行,且存在直线与![]() 垂直
垂直
(B)![]() 内不一定存在直线与
内不一定存在直线与![]() 平行,不一定存在直线与
平行,不一定存在直线与![]() 垂直
垂直
(C)![]() 内不一定存在直线与
内不一定存在直线与![]() 平行,但必存在直线与
平行,但必存在直线与![]() 垂直
垂直
(D)![]() 内必存在直线与
内必存在直线与![]() 平行,却不一定存在直线与
平行,却不一定存在直线与![]() 垂直
垂直
15.已知集合![]() ,若
,若![]() 则
则
![]() 与集合
与集合![]() 的关系是
( )
的关系是
( )
(A)![]()
![]() 但
但![]() (B)
(B)![]()
![]() 但
但![]() (C)
(C)![]()
![]() 且
且![]() (D)
(D)![]()
![]() 且
且![]()
16.某幢楼从二楼到三楼的楼梯共10级,上楼可以一步上一级,也可以一步上两级,若规定从二楼到三楼用8步走完,则上楼梯的方法有 ( )
(A)45种 (B)36种 (C)28种 (D)25种
三、解答题(36分)
17.(8分)已知数列![]() 其前
其前![]() 项和为
项和为![]() ,且
,且![]() ,当
,当![]() 时,
时,![]() 。
。
(1)求数列![]() 的通项公式。 (2)若
的通项公式。 (2)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() 。
。
18.(8分)在![]() 中,
中,![]() , 求角
, 求角![]() 的范围。
的范围。
19.(10分)有一组数据![]() 的算术平均值为10,若去掉其中最大的
的算术平均值为10,若去掉其中最大的
一个,余下数据的算术平均值为9;若去掉其中最小的一个,余下数据的算术平均值为11。 (1) 求出第一个数![]() 关于
关于![]() 的表达式及第
的表达式及第![]() 个数
个数![]() 关于
关于![]() 的表达式。
的表达式。
(2) 若![]() 都是正整数,试求第
都是正整数,试求第![]() 个数
个数![]() 的最大值,并举出满足题目要求且
的最大值,并举出满足题目要求且![]() 取到最大值的一组数据。
取到最大值的一组数据。
20.(10分)已知函数![]() ,满足条件: ①
,满足条件: ①![]() ;②
;②![]() ;
;
③![]() ; ④当
; ④当![]() 时,有
时,有![]() 。 (1)求
。 (1)求![]() ,
,![]() 的值。
的值。
(2)由![]()
![]() ,
,![]() 的值,猜想
的值,猜想![]() 的解析式。 (3)证明你猜想的
的解析式。 (3)证明你猜想的![]() 的解析式的正确性。
的解析式的正确性。
高三数学测试题(6)参考答案
一、填空题
1.4 2.0 3.![]() 4.
4.![]() 5.12 6.
5.12 6.![]() 7.
7. ![]() 8.①或② 9.
8.①或② 9.![]() 10.3
10.3
11.![]() 12.14
12.14
二、选择题
13.C 14.C 15.B 16.C
三、解答题
17.(1)当![]() =1时,
=1时,![]() ;当
;当![]() =2时,有
=2时,有![]() ;当
;当![]() 时,有:
时,有:
![]() .故该数列从第2项起为公比q=2的等比数列,
.故该数列从第2项起为公比q=2的等比数列,
故![]() (2)由(1)知
(2)由(1)知 ![]()
故数列![]() 的前
的前![]() 项和
项和 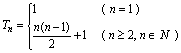
18.
解:由![]()
![]() =
=![]() 得:
得:![]() ,即
,即
![]() ,∴
,∴![]() ,即
,即![]() 。由余弦定理,得:
。由余弦定理,得:
![]() ,∵
,∵![]() 且函数
且函数![]() 在
在![]() ]上是减函数
∴
]上是减函数
∴![]() ,即
,即![]() 的范围是
的范围是![]() 。
。
19.解: (1) 依条件得: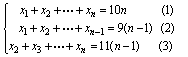 由
由![]() 得:
得:![]() ,又由
,又由![]() 得:
得:![]() (2)由于
(2)由于![]() 是正整数,故
是正整数,故 ![]() ,
,![]() ,故
,故![]() 当
当![]() =10时,
=10时, ![]() ,
,![]() ,
,![]() , 此时,
, 此时,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 。
。
20.解:(i):∵![]() ,又
,又![]() ,∴
,∴![]() 。又∵
。又∵![]() ,
,
![]() ,且
,且![]() 。∴
。∴![]() 。
。
(ii)由![]() 猜想
猜想![]() 。
。
(iii)用数学归纳法证明:
(1)当![]() =1时,
=1时,![]() ,函数解析式成立;
,函数解析式成立;
(2)假设![]() 时,
时,![]() ,函数解析式成立;
,函数解析式成立;
①若![]() ,
, ![]() 。
。
②若![]() ,
, ![]() ,
,
![]() 。∴
。∴![]() 。
。
即![]() 时,函数解析式成立。
时,函数解析式成立。
综合(1)(2)可知,![]() 成立。
成立。