高三数学测试题（7）
班级____________姓名____________学号____________成绩____________
一、填空题（48分）
1．
=
.
2．已知
是坐标原点，经过
且与
垂直的直线方程是________________.
3．已知两点
，点P满足
，则点P的轨迹方程为____________.
4．设
是椭圆
的两个焦点，点P在椭圆上，且
，则△F1PF2的面积
为 .
5．某校高一年级有400人，高二年级有320人，高三年级有280人，若以每人被抽取的概率为
0.2，从该校高中学生里抽取一个容量为n的样本，则n= .
6．已知
，则直线
的倾斜角的取值范围是_______________.
7．圆
在
轴上截得的弦长为____________.
8．若
，点
满足方程
，则由点
组成的图形的面积
为_________.
9．直线
与圆
的位置关系是
.
10．已知△ABC中，点D在BC边上，且
则
的值是 .
11．设
，则n的值为
.
12．设x、y是两个实数，给出下列五个条件：①
；②
；③；
;
④
；⑤
. 其中能推出“x、y中至少有一个数大于1”的条件是 .
二、选择题（16分）
13．方程 x (x2 + y2－3) = 0与x2 + (x2 + y2－3)2 = 0所表示的曲线是 ( )
(A) 都表示一条直线和一个圆 (B) 前者是两个点，后者是一条直线和一个圆
(C) 都表示两个点 (D) 前者是一条直线和一个圆，后者是两个点
14．已知
是大小确定的一个二面角，若a,b是空间两条直线，则能使a,b所成的角为定值的一个条件是
（ ）
(A) 
(B) 
(C) 
(D) 
15． 方程
表示的曲线是
（ ）
(A) 两个外切的圆； (B) 两个外切的半圆；
(C) 两个相离的圆； (D) 两个相离的半圆.
16．由方程
确定的函数
在
上是
( )
(A) 奇函数 (B) 偶函数 (C) 增函数 (D) 减函数
三、解答题（8+8+10+10=36分）
17.已知过点P的直线l绕点P按逆时针方向旋转
角(
)，得直线为
，若继续按逆时针方向旋转
角，得直线
，求直线l的方程.
18．已知数列
满足
.
(1)求证：数列{bn+2}是公比为2的等比数列； (2) 求
.
19．一片森林面积为a，计划每年砍伐一批木材，每年砍伐面积的百分比相等，则砍伐到原面积的一半时，所用时间是T年．为保护生态环境，森林面积至少要保留原面积的25％．已知到今年止，森林剩余面积为原来的
．
(1) 问到今年止，该森林已砍伐了多少年？ (2) 问今后最多还能砍伐多少年？
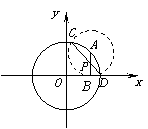20．已知A是圆
上任一点，AB垂直于
轴，交轴于点B．以A为圆心、AB为半径作圆交已知圆于C、D，连结CD交AB于点P，求点P的轨迹方程．
高三数学测试题（7）参考答案
一、填空题（48分）
1．
; 2．
; 3．
; 4．1;
5．200; 6．
; 7．2;
8．
; 9．相切;
10．0; 11．6;
12．③.
二、选择题（16分）
13．D; 14．D; 15．D; 16．D
三、解答题（8+8+10+10=36分）
17. 由
得
据题意，直线l与直线
垂直，故l斜率
∴ 直线l方程为 
, 即
.
18．（1）由
是公比为2的等比数列.
（2）由（1）可知
令n=1，2，…n－1，则
，
各式相加得
.
19．设每年砍伐面积的百分比为
. 则 
， ∴ 
，
．
(1) 设到今年为止，该森林已砍伐了x年，∴ 
，
于是 
，表明已砍伐了
年．
(2) 设从开始砍伐到至少保留到原面积的25％，需y年．
∴ 
，∴ 
y ≤ 2T．
因此今后最多还能砍伐的年数为 
．
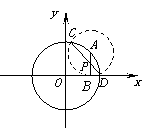20．设点A的坐标为A(2cosa，2sina)，则以A为圆心、AB为半径的圆的方程为:
(x－2cosa)2 + (y－2sina)2 = 4sin2a．
联立已知圆的方程，相减，可得公共弦CD的方程为:
xcosa + ysina = 1+ cos2a． (1)
而AB的方程是 x = 2cosa． (2)
所以满足(1)、(2)的点P的坐标为(2cosa，sina)，消去a，即得
点P的轨迹方程为
．
说明： 设A(m，n)亦可类似地解决．