高三数学第一学期期末练习
数 学
一、选择题：本大题共8个小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1．若
，则 （ ）
A．
B．
C．
D．
2．已知直线
与直线
互相垂直，则实数a
的值为 （ ）
A．－1或2 B．－1或－2 C．1或2 D．1或－2
3．已知m,l是异面直线，那么
①必存在平面α，过m且与l平行； ②必存在平面β，过m且与l垂直；
③必存在平面γ，与m，l都垂直； ④必存在平面π，与m，l的距离都相等.
其中正确的结论是 （ ）
A．①② B．①③ C．②③ D．①④
4．（理）要得到函数y=sin2x的图象，可以把函数
的图象 （ ）
A．向左平移
个单位 B．向右平移个单位
C．向左平移
个单位 D．向右平移个单位
（文）要得到函数的图象，可以把函数y=sin2x的图象 （ ）
A．向左平移个单位 B．向右平移个单位
C．向左平移个单位 D．向右平移个单位
5．设圆锥的母线与其底面成30°角，若圆锥的轴截面的面积为S，则圆锥的侧面积等于（ ）
A．
B．
C．2 D．4
6．已知点A（－2，0）及点B（0，2），C是圆x2+y2=1上一个动点，则△ABC的面积的最
小值为 （ ）
A．2
B．2+
C．2 D．
7．（理）从8盆不同的鲜花中选出4盆摆成一排，其中甲、乙两盆不同时展出的摆法种数为
（ ）
A．1320 B．960 C．600 D．360
（文）从8盆不同的鲜花中选出4盆摆成一排，其中甲、乙两盆有且仅有一盆展出的不同摆法种数为 （ ）
|
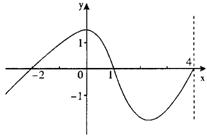
8．设函数f(x)的定义域[－4，4]，其图象如图，
那么不等式
的解集为（ ）
A．[－2，1]
B．[－4，－2]∪[1，4]
C．[－4，－π]∪[－2，0]∪[1，π]
D．不同于（A）、（B）、（C）
二、填空题：本大题共6个小题，每小题5分，共30分.把答案填在题中横线上.
9．在△ABC中，AB=2，BC=3，AC=
，则△ABC的面积为
，△ABC的外
接圆的面积为 .
10．在公差为d（d≠0）的等差数列{an}及公比为q的等比数列{bn}中，已知a1=b1=1，a2=b2，
a8=b3，则d= ；q= .
11．（理）设a，b都是正实数，且2a+b=1，设T=
则当a= 且b= 时，T的最大值为 .
（文）设a，b都是正实数，且a+b=1，设T=
则当a= 且b= 时，T的最大值为 .
12．设函数
函数
且
的图象过点A（4，－5）及B（－2，－5），则a=
；函数
的定义域为
.
13．（理）定义运算：
，若复数
满足
的模等于x，则复数z对应的Z（x，y）的轨迹方程为
；其图形为
.
（文）定义运算：，若复数满足=2，
则x ；y= .
|
，AD=1，在DC上截取
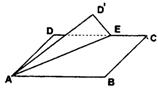
DE=1，将△ADE沿AE翻折到D′点，当D′在平面ABC
上的射影落在AE上时，四棱锥D′—ABCE的体积是 ；
当D′在平面ABC上的射影落在AC上时，二面角D′—AE
—B的平面角的余弦值是 .
三、解答题：本大题共6个小题，共80分.解答应写出文字说明、证明过程或演算步骤.
15．（本小题满分12分）
已知：函数
.
（Ⅰ）求函数f(x)的最小正周期；
（Ⅱ）当函数f(x)取得最大值时，求自变量x的集合.
16．（本小题满分12分）
（理科学生做）解关于
的不等式：
.
（文科学生做）解不等式：
.
17．（本小题满分16分）
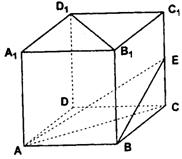
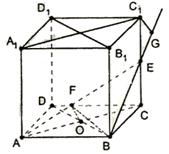
在正方体ABCD—A1B1C1D1，棱长AA1=2.
（Ⅰ）E为棱CC1的中点，求证：B1D1⊥AE；
（Ⅱ）（理科学生做）求二面角C—AE—B的平面角的正切值；
（文科学生做）求二面角E—AB—C的平面角的正切值；
|
18．（本小题12分）
有一组数据：
它们的算术平均值为10，若去掉其中最大的一个，余下的数据的算术平均值为9；若去掉其中最小的一个，余下数据的算术平均值为11.
（Ⅰ）求出第一个数
关于n的表达式及第n个数
关于n的表达式.
（Ⅱ）若
都是正整数，试求第n个数的最大值，并举出满足题目要求且取到最大值的一组数据.
19．（本小题满分16分）
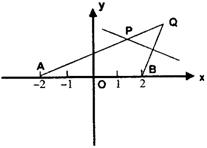
在直角坐标平面内，已知两点A（－2，0）及B（2，0），动点Q到点A的距离为6，线段BQ的垂直平分线交AQ于点P.
（Ⅰ）证明PA+PB为常数，并写出点P的轨迹T的方程；
（Ⅱ）（理科学生做）过点B的直线l与曲线T相交于M、N两点，线段MN的中点R与点S（－1，0）的连线的纵截距为t，试求t的取值范围.
|
20．（本小题满分12分）
已知定义域为[0，1]的函数f(x)同时满足：
（1）对于任意
；
（2）f(1)=1
（3）若
（Ⅰ）试求f(0)的值；
（Ⅱ）试求函数f(x)的最大值；
（Ⅲ）（理科学生做，文科学生不做）
试证明：满足上述条件的函数f(x)对一切实数x，都有
.
高三数学参考答案及评分标准
一、选择题（每小题5分，共40分）
1.C 2.B 3.D 4.理A 文B 5.C 6.A 7.理A 文B 8.D
二、填空题（每小题5分，其中第一空3分，第二空2分，共30分.）
9．
10．5；6 11．理：
文：
12．2；－1<x<3 13．理：
抛物线 文：3；0 14
三、解答题（共80分）
15．（本题满分12分）
解：
…………3分 =sin2x－cos2x …………5分
=
…………7分 ∴
的最小正周期T=π …………8分
当取得最大值时，只须
…………10分
即
∴当
取得最大值时，自变量x的集合为
……12分
16．（本题满分12分）
（理科）解：原不等式可以化成
…………2分
（Ⅰ）当a>1时，原不等式为
上述不等式
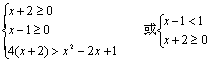…………5分
解得：
即 
…………7分
（Ⅱ）当0<a<1时，原不等式为
上述不等式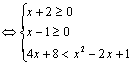
…………9分
解得：x>7 …………12分 综合（Ⅰ）（Ⅱ）可得
当a>1时，原不等式的解集为
当0<a<1时，原不等式的解集为
（文科）解：原不等式可以化成
…………2分
即 
…………4分 上述不等式
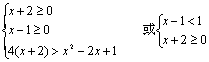…………8分
解得： …………12分
即原不等式的解集为 
17．（本题满16分）
（1）证明：连结A1C1. ∵AA1⊥平面A1C1 ∴A1C1是AE在平面A1C1上的射影.
在正方形A1B1C1D1中，B1D1⊥A1C1 ∴B1D1⊥AE …………5分
|
交AE于F，连结OF. ∵EC⊥平面AC，
在正方形ABCD中，BD⊥AC，∴BD⊥平面ACE.
∴OF是BF在平面EAC上的射影，∴AE⊥FO.
∴∠BFO是二面角B—AE—C的平面角.……9分
在正方形ABCD中，BO=AO=
，
在Rt△ACE中，AE=3，∵△AOF∽△AEC，
∴ 
∴
在Rt△BOF中，
…………11分
（文科）∵AB⊥平面BC1，BE
平面BC1，BC平面BC1， ∴BE⊥AB，BC⊥AB，
∠EBC是二面角E—AB—C的平面角.…………9分
在Rt△ECB中，
…………11分
（3）过C1作C1G⊥BE交BE的延长线于G， ∵AB⊥平面BC1，C1G平面BC1，
∴ AB⊥C1G，∴C1G⊥平面ABE. ∵D1C1//AB，D1C1
平面ABE，
∴D1C1//平面ABE. ∴D1到平面ABE的距离等于C1到平面ABE的距离……14分
∵
△C1GE∽△BCE， ∴
∴
∴ D1到不在ABE的距离等于
…………16分
18．（本题满分12分）
解：依条件：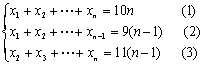
…………3分
（Ⅰ）由（1）－（2）得：
再（1）－（3）得：x1=11－n……6分
（Ⅱ）∵x1是正整数，∴x1=11－n≥1，
，∴xn=n+9≤19…………10分
当n=10时，
此时，取
即可,
∴当n=10时，xn的最大值是19.………………12分
19．（本题满分16分）
解：（Ⅰ）连结PB. ∵线段BQ的垂直平分线与AQ交于点P，
∴PB=PQ. 又AQ=6， ∴PA+PB=PA+PQ=AQ=6 （常数）.…………2分
又PA+PB>AB，从而P点的轨迹T是中心在原点，以A、B为两个焦点，长轴在x轴上的椭圆，其中，2a=6，2c=4， ∴椭圆方程为
…………6分
（Ⅱ）（理科）当直线l与x轴垂直时，MN的中点为R（2，0）
直线RS的纵截距t=0 …………7分
当直线l与x轴不垂直时，设其斜率为k， 点M
.
由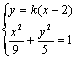
，消去y整理得：
…………9分
∴
， 则
直线RS的方程为
.
令x=0，可得直线RS的纵截距 
如果k=0，则t=0；
如果k≠0，则
∵
当且仅当
时，等号成立.…………14分
∴
综上可知，所求t的取值范围是 [－
，].…………16分
（文科）直线l斜率
，又l过B（2，0）点，其方程为
由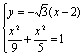
，消去y整理得： 32x2－108x+63=0 …………9分
设点M
则
MN=
=2
…………12分
点A（－2，0）到直线l的距离为d，则
……14分
∴△AMN的面积为 
…………16分
（注：本题也可以用
求解，参照以上评分标准给分）
20．（本题满分12分）
（Ⅰ）令
依条件（3）可得
又由条件（1）得
…………理：3分. 文：5分
（Ⅱ）任取
则
……理：5分. 文：8分
即 
于是当
因此，当x=1时，f(x)有最大值为1.…………理：7分. 文：12分
（Ⅲ）（理科）证明：研究①当
②当
，
首先，
…………9分
显然，当
时，
成立.
假设当
时，有
成立，其中k=1，2，…那么当
时，
可知对于
，总有
其中n=1，2，…而对于任意
存在正整数n，使得
此时
…………11分
③当x=0时，
…………12分
综上可知，满足条件的函数
总有成立.
（囿于篇幅，若有其它正确解法请按相应步骤给分.）