高三函数(二)测验

高三函数(二)测验　　

　　　　　　　 班级　　　　 学号　　 姓名　　　　 

一、填空题

1、函数的定义域是　　　　　　　　　　　　　　　　　　　　.

2、函数的递减区间是　　　　　　　　　　　　　　　　　　　　.

3、若关于有唯一解，则实数的取值范围是　　 .

4、若函数对任意都有，则的取值范围是

　　　　　　　　 .

5、函数的图象经过点（1，3），且其反函数的图象经过点（2，0），则函数的表达式为　　　　　　　 .

6、若函数在区间上的最大值是最小值的3倍，则a=　　　　．

7、函数的最大值是　　　　 ．

8、已知f(x)=,则不等式x+(x+2)·f(x+2)≤5的解集是__________.

9、函数是幂函数，且当时为减函数，则实数m的值为　　　　　　　　 ．

10、奇函数f(x)的定义域是R，函数。若g(1)=4，则g(-1)的值等于　　　 .

11、定义在R上的偶函数在是单调递减，若，则的取值范围是___________．

12、设函数f(x)=xx+bx+c，给出四个命题：①c=0时，f(x)是奇函数；②b=0,c>0时，方程f(x)=0只有一个实根；③f(x)的图象关于点（0，c）对称；④方程f(x)=0至多有两个实根，其中正确命题的序号是____________.

二、选择题

13、若0<a<1，则log_0.5a,log₃a,log₅a三者的大小关系为　　　　　　 (　 )

　 A． log_0.5a>log₅a> log₃a　　　　　 B． log₅a> log₃a >log_0.5a

　 C． log₃a >log₅a>log_0.5a　　　　　 D． log_0.5a> log₃a>log₅a

14、若函数y=f(x)的定义域是[－1,1],则函数y=f(lgx－1)的定义域是  (　 )

A．(0,＋∞)　　 B．(0,100]　　　C．[1,100]　　　D．[2,＋∞)

15、方程的解集为N，则M，N的关系是　　　　　　　　　　　　　　　　　　　　　　　 （　 ）

　　A. M=N　　B. 　　C. 　　D.

16、函数y＝－e^x的图象　　　　　　　　　　　　　　　　　　  （　 ）

A．与y＝e^x的图象关于y轴对称　B.与y＝e^x的图象关于坐标原点对称

C.与y＝e^－x的图象关于y轴对称　D.与y＝e^－x的图象关于坐标原点对称

17、函数f(x)=x²-2ax-3在区间[1，2]上存在反函数的充分必要条件是 (　　)

A．a∈（-∞，1　　　　　　 B．a∈2，+∞）

C．a∈[1，2]　　　　　　　　 D．a∈（-∞，1∪2，+∞）

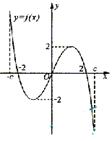
18、f()是定义在区间[－c,c]上的奇函数，其图象如图所示：

令g（）=af（）+b，则下列关于函数g（）的叙述正确的是　（　　）

A．若a<0,则函数g（）的图象关于原点对称.

　　　　　　　　　　　　　　　　　　　 B．若a=－1，－2<b<0,则方程g（）=0有大于2的实根.

　　　　　　　　　　　　　　　　　　　 C．若a≠0,b=2,则方程g（）=0有两个实根.

　　　 D．若a≥1,b<2,则方程g（）=0有三个实根

三、解答题

19、利用函数单调性定义，证明函数在（0，1）上是增函数.

20、已知是函数的反函数，且，都有意义，试比较2与4的大小，并说明理由.

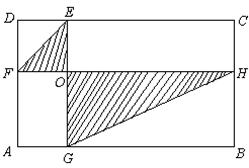
21、如图所示，长方形ABCD中，上分别取E、F，使∥∥AB，的面积和为S。

　　　 （1）求的表达式和该函数定义域；

　　　 （2）求的最小值。

22、已知的最大值与最小值

答案

1、[1，2）　　　　 2、　　3、　　 4、{－10，10}

5、　　6、　　7、　  8、　　　 9、2　　

10、-2　 11、a<0或a>3　 12、①②③

13、A　 14、C　 15、A　 16、D　 17、D　 18、B

19、解：任取则

　　　　　　　

　　　 ∴　

　　　 又函数上是增函数，

　　　 ∴　

　　　 ∴　 在（0，1）上是增函数。

20、解：由已知可得

　　　 由　 有意义，有

　　　 解之可得

　　　 并且

　　　　　　　

　　　 又　 。

　　　 ∴　 当

　　　　　　　当。

　　　 而函数是减函数；

　　　 ∴　 当

　　　　　　　　当_.

21、解：（①　　

　　　　　　　　

　　　 ∵　 ，其定义域为

　　　 ②　

　　　 又　

　　　 且　

　　　 ∴　 当时，S最小值为；

　　　　　　　当时，S最小值为。

　　　 注：若认为函数定义域为（0，b），则当时, 无最小值．

22、

　　.