高三年级圆锥曲线测试题
一．
选择题（
）
1．若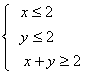
，则目标函数u＝x－2y的最大值是 ( )
A、－4 B、－2 C、2 D、4
2．直线
和
的斜率分别是方程
的两根，那么和
的夹角等于 （ ）
A、165°； B、15°； C、75°； D、105°
３．平面内与定点
和直线
的距离相等的点的轨迹是（ ）．
A．椭圆 B．双曲线 C．抛物线 D．直线
４．已知椭圆
，定点
，则椭圆以
为中点的弦所在的直线的斜率等于（ ）
A．
B．
C．
D．
5．若抛物线
上一点到准线和抛物线的对称轴的距离分别为10和6，则该点的横坐标为 （ ）
A．10 B．9 C．8 D．7
6．设F1、F2是双曲线
的两个焦点，点P在双曲线上，∠F1PF2=90°若△F1PF2的面积为1，则a的值是 （ ）
A．1 B．
C．2 D．
7．直线
与双曲线
的左支有且仅有一个公共点，则
的取值范围是（ ）．
A．
B．
或
C．
或 D．
或
8．抛物线的顶点是圆
的圆心，抛物线与圆的公共弦是抛物线的通径（即过焦点且垂直于对称轴的弦），则（ ）．
A．
B．
C．
D．
9．直线
与曲线
的交点的个数是（ ）
A．0 B．1 C．2 D．3
10．设
，
当
时，r的取值范围是
（ ）
A、
B、
C、
D、
11．已知
是椭圆
的两个焦点，是椭圆上的点，当
，且
面积最大时，则有（ ）
A．
B．
C．
D．
12．方程
表示的曲线是
（ ）
A、椭圆 B、双曲线 C、两条直线 D、两条射线．
| 题号 | ||||||||||||
| 答案 |
二．填空题（
）
13.已知方程
所表示的图形是焦点在x轴上的椭圆，则k的取值范围是_____________________________________．
14. 已知直线
，若
与两坐标轴围成的四边形有外接圆则k的取值是
。
15．已知椭圆E的离心率为e，两焦点
，抛物线c以
为顶点、以
为焦点，P为两曲线的一个交点，若
，则离心率
的值为_________．
16．设x、y满足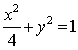
，则
的最大值为___________
三．解答题
17．已知直线
与椭圆
相交于A、B两点，且线段AB的中点在直线
上。（Ⅰ）求此椭圆的离心率；
（Ⅱ）若椭圆的右焦点关于直线
的对称点的在圆
上，求此椭圆的方程。
18．设圆
的方程为：
，
①、求圆心C的轨迹；②圆心的轨迹过点
，圆中的最大圆和最小圆的公共弦所在直线为
，求
的值．
19．直线
与双曲线C：
恒有公共点。
（1）求双曲线的离心率的取值范围；
（2）若直线
过双曲线C的右焦点F，与双曲线交于P、Q两点，并且满足
，求双曲线C的方程。
20．如图已知Rt△ABC的顶点B（-3，0），点C在y轴上，点A在x的正半轴上，且
，点Q满足
．
（1）当C在y轴上移动时，求动点Q的轨迹E方程．
（2）圆D：
，过曲线E上的一点P作圆的两条切线，切点分别为Ｍ、Ｎ，求四边形PMDN面积的最小值．
（3）在问题（2）中求AB所在的直线方程．
21、已知曲线C：
(θ为参数)，若A、B是曲线C上关于坐标轴不对称的任意两点.
（1）求AB的垂直平分线l在x轴上截距的取值范围；
（2）设过点M（1，0）的直线l是曲线C上A，B两点连线的垂直平分线，求l的斜率k的取值范围.