高三上学期期中考试数学试题答案

高三上学期期中考试数学试题答案

一： 选择题答案

1	2	3	4	5	6	7	8	9	10	11	12
C	C	B	C	B	D	A	B	C	D	D	C

二　.填空题:

13.(0,4)　　　 14.　　　　　 15.(文)a　 (理)　　　　 16.a≥

三.  解答题:

17.　 (1)由a=a_n+,a₁=1,知a₂=1　又由递推式变形为：

（n+1）n a=（n-1）n a_n+2 .记（n-1）n a_n=b_n ,则b= b_n+2，又b₂=2a₂=2

b_n=b₂+(n-2)2=2+2(n-2)=2(n-1).于是有（n-1）na_n=b_n=2(n-1),(n≥2)　从而a_n=（n≥2）

因此a_n=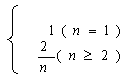

　  (2)求和 a₁a₂+a₂a₃+a₃a₄+…+a_na=1﹒+(﹒+﹒+…+﹒) =3-

 18.(文)(1)由已知f(x)=0的两根为-3和2。

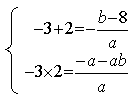
a=-3,b=5

f(x)=-3x²-3x+18=-3(x+)²+18,f_max=f(0)=18,f_min=f(1)=12

f(x)[12,18]

　　　　　 (2)-3x²+5x+c0,=25+12c0,c-　　　　　　　　　　　　　　　

(理)解：（1）y^/=1+=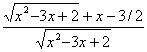,当x<1时，y^/<0恒成立。f(x)在（-，1是

　减函数。

　　　 （2）（x+）===

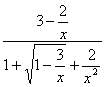19.　解:令3+2sincos=n,asin+acos=m,原题转化为要使(x+m)+(x+n)恒成立.

　　 即需2x²+2(m+n)x+m²+n²-0恒成立.

从而只需=[2(m+n)]²-4•2(m²+n²-)0,即需(m-n)²恒成立, 即m-n.或m-n-

于是：asin+acos-(3+2sincos)或-………………………………(1)　　　

令t= sin+cos,则sincos=(t²-1)且1t.

 (1)式化为：at3+t²-1+或at3+t²-1-

即a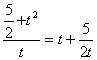或at+恒成立. 又f(t)=t+在1t上为减函数，

即g(t)=t+在1t上最小值为，于是a1+5/2=7/2或a。

因此所求a的值为a7/2或a。

　　20.　(1)设P(x,y)是f(x)图象上任一点，点P关于直线y=x-1的对称点为Q(a,b)

　　　　 则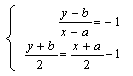，解得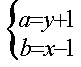

即Q(y+1,x-1),又点Q在y=2-a-1的图象上，故x-1=2-a-1。

由此得f(x)=2log₂(x+a)+1.又f(0)=1,可得a=1

f(x)= 2log₂(x+1)+1,定义域为{x∣x>-1}

(2)由(1),要证明f(m)+f(n) 2f(t), 即证log₂(m+1)+log₂(t+1) 2log₂(n+1)

　　　　  只要证明log₂[(m+1)(t+1)] log₂(n+1)² 

函数y=log₂x在(0,+ )上是增函数,只要证明(m+1)(t+1)  n+1)²

　　　　  由已知有n²=mt,故只要证明m+t2t

　　　　  而m+t2=2=2n²是成立的.　　原不等式得证.

21.　　　解：（1）设该校食堂平均每天所支付的总费用为y₁,则

y₁=[4t1500+4t(t+1)+400]=4t++60042

　　　 　当且仅当4t=，即t=10时等号成立，故每隔10天购买一次大米，能使每天所支付的总费用最少为6084元。

　　　　（2） 若食堂能接受优惠条件，则至少每隔20天购买一次，即t20，设每天支付的总费用为y₂,这时，

y₂=[4t(t+1)+400+4t15000.95]=4t++5704,

令f(t)= 4t+(t20) ,设20t₁<t₂ ,则

f(t₁)-f(t₂)=  <0

所以f(t)在 上是增函数，故当t==20时，y₂的最小值是5804元。这就是说该校食堂是能

接受此价格优惠条件的。

22．解 ：（1）由f(4-x)=f(4+x)知y=f(x)关于直线x=4对称，

　　　　　　　 所以有：=4解得p=6

　　　　  (2)f(x)=x²-8x+q²-q+1=(x-4)²-16+q²-q+1=(x-4)²+q²-q-15

　　　　　　 对称轴x=4,在[-1,1]上f(x)为单调递减函数.由题意f(x) <0

　　　　　　 即(1-4)²+q²-q-15<0　， 整理得 ：(q-3)(q+2) <0　-2<q<3

　　　　  （3）x时，f(x) D　　　 ①当3<t<4时 , f(x)递减,f_max=f(3)=-15+q²-q+1,

　　　　　　  f_min=t²-8t+q²-q+1,  f_max- f_min =-15-t²+8t=2t, t²-6t+15=0,  =36-60<0

　　　　　  　无解。　　②当4t5时， f_max= f(3)，f_min = f(4)

　　　　　　 f(3)-f(4)=1=2t, t=（舍）　　　 ③t>5时，f_max= f(t), f_min = f(4)

　　　　　　 t²-8t+q²-q+1-q²+q+15=2t,　　t²-10t+16=0　,t=8或t=2（舍）

　　　　　 存在t=8，当x 时, y=f(x) 的值域为区间D，且D的区间长度为16.

　　　 附：

　  一：已知二次函数y=f(x)经过点(0,10)导函数f^/(x)= 2x-5，当x(nN₊)时，f(x)是整数的个数记为a_n.

(1)　　求数列{a_n}的通项公式。

(2)　　令b_n=,求数列{a_n+b_n}的前n(n3)项和S_n

二．设函数f(x)=(1+x)²-ln(1+x)²

1.　　　 求f(x)的单调区间。

2.　　　 若当x[-1，e-1]时，不等式f(x)<m恒成立，求实数m的取值范围。

3　.若关于x的方程f(x)=x²+x+a在区间上[0,2]恰好有两个相异的实根，求实数a的取值范围。

　 解答

一．解（1）设f(x)=ax²+bx+10,则f^/(x)=2ax+b.由已知，f^/(x)=2x-5, a=1,b=-5.  f(x)=x²-5x+10,

f(x)在上的值域为 a₁=2， f(x)在上的值域为 ，a₂=1 ，当n3时，f(x)在上

　　　　单调递增，其值域为　a=

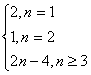
(3)　令c_n=a_n+b_n，则c₁=a₁+b₁=4,c₂=a₂+b₂=3.　当n3时，s_n=c₁+c₂+(c₃+c₄+…c_n)=…=n²-3n+

二．解：[1]函数的定义域为（-，-1）（-1，+）， f^/(x)=2[（x+1）-]=,由 f^/(x)>0得

-2x<-1，或x>0. 由 f^/(x)<0得-1x<0，或x<-2,则递增区间为（-2，-1），（0，+）。递减区间是　　　　　　　　 （-，-2），（-1，0）

  [2]　由f^/(x)= =0得x=0或x=-2由（1）知，f(x)在[-1，0]上递减，在[0，e-1]上递增，又f(-1)

=+2,f(e-1)=e²-2,且e²-2>+2x[-1,e-1]时,f(x)= e²-2，故m> e²-2时，不等式f(x) <m恒成立。

[3]　方程f(X)=x²+x+a,即x-a+1-ln(1+x)²=0.记g(x)=x-a+1-ln(1+x)²g^/(x)=1-=

　 由g^/(x)>0得x>1或x<1，由g^/(x)<0得-1<x<1，g(x)在[0，1]上递减，在[1，2]上递增，为使f(X)=x²+x+a

在[0，2]上恰好有两个相异的实根，则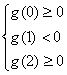解得2-2ln2<a3-2ln3