高三数学40分钟小测试卷数列
———数列（Ⅰ） 试卷总分100分
班级____________姓名_______________座号___________评分____________
一、选择题(每题5分,共40分)
1.已知数列1，
，
，…，
…，则其通项的表示为( )
A.｛an｝ B.｛｝ C.
D.n
2.已知数列｛an｝中，an=4n-13·2n+2，则50是其( )
A.第3项 B.第4项
C.第5项 D.不是这个数列的项
3.已知数列的通项公式an=2n-1，则2047是这个数列的( )
A.第10项 B.第11项 C.第12项 D.第13项
4.数列-1，
，-
，
，…的通项公式是( )
A.an=(-1)n
B.an=(-1)n
C.an=(-1)n
D.an=(-1)n
5.在数列a1,a2,a3,…，an，…的每相邻两项中插入3个数，使它们与原数列构成一个新数列，则新数列的第29项( )
A.不是原数列的项 B.是原数列的第7项
C.是原数列的第8项 D.是原数列的第9项
6.已知数列的通项公式为an=
，则an与an+1的大小关系是( )
A.an＜an+1 B.an＞an+1
C.an=an+1 D.大小不能确定
7.数列｛an｝中，an=-2n2+29n+3，则此数列的最大项的值是( )
A.107 B.108 C.108
D.109
8.数列1，3，6，10，15，…的通项公式an等于( )
A.n2-(n-1) B. 
C. 
D.n2-2n+2
二、填空题(每题5分共20分)
1.数列-，
，-
，…的一个通项公式是
.
2.数列1，1，2，2，3，3，…的一个通项公式是 .
3.已知数列｛an｝满足a1=1,an+1=pan+q，且a2=3,a4=15,则p= ,q= .
4.一个数列的前n项之和是nn，则此数列的第4项为 .
三、解答题
１. 已知数列的通项公式为an=-0.3n2+2n+7
，求它的数值最大的项.(8分)
２. 若数列｛an｝由a1=2，an+1=an+2n(n≥1)确定，求通项公式an. (8分)
3．参加一次国际商贸洽谈会的国际友人居住在西安某大楼的不同楼层内，该大楼共有n层，每层均住有参会人员.现要求每层指派一人，共n人集中到第k层开会，试问k如何确定，能使n位参加会议人员上、下楼梯所走路程总和最少?(假定相邻两层楼楼长都相等) (12分)
4.某人从A地到B地乘坐出租车，有两种方案：第一种方案：利用起步价10元，每千米价为1.2元的汽车.第二种方案：租用起步价是8元，每千米价为4元的汽车.按出租车管理条例，在起步价内，不同型号车行驶的里程是相等的.则此人从A地到B地选择哪一种方案比较合适. (12分)
数列（Ⅰ）参考答案：
一、1.C 2.B 3.B 4.D 5.C 6.A 7.B 8.C
二、1.an=
2.an=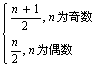
3.2或-3，1或6 4.229
三、1.最大的项为a3=
2.an=2+n(n+1)
3、当n为奇数时，取k=
，S最小；
当n为偶数时，取k=
或
，S最小.
4、解：设起步价内行驶里程为a千米，A地到B地的距离是m千米.
当m≤a时，选起步价8元的出租车比较合适.
当m＞a时，设m=a+x(x＞0)
乘坐起步价10元的出租车费用为P(x)元，乘坐起步价为8元的费用为Q(x)元，
则：P(x)=10+1.2x
Q(x)=8+1.4x
令P(x)=Q(x)得10+1.28+1.4x解得x=10(千米)
此时两种出租车任选.
当x＞10时，P(x)-Q(x)=2-0.2x＜0，故P(x)＜Q(x)
此时选起步价为10元合适.
当x＜10时，P(x)-Q(x)=2-0.2x＞0，故P(x)＞Q(x)
此时选起步价为8元的出租车合适.