高三数学《回归课本》（一上）
一、选择题
1．如果X = ，那么(一上40页例1(1))
(A) 0 Í X
(B) {0} Î X (C) F Î X (D)
{0} Í X
2．ax2
+ 2x + 1 = 0至少有一个负实根的充要条件是(一上43页B组6)
(A)0<a≤1 (B)
a<1 (C)
a≤1 (D)
0<a≤1或a<0
3．命题p：“a、b是整数”，是命题q：“ x 2
+ ax + b = 0 有且仅有整数解”的
(A) 充分不必要条件
(B) 必要不充分条件
(C) 充要条件 (D) 既不充分也不必要条件
4．若y = x + b与y = ax + 3互为反函数，则 a + b =
(A) －2
(B) 2
(C) 4 (D) －10
5．已知x + x – 1 = 3，则
+ 
的值为
(A) 3 (B)
2 (C)
4 (D) －4
6．下列函数中不是奇函数的是
(A) y
= (B)
y = (C) y = (D)
y = log a
7．下列四个函数中，不满足f()≤的是
(A) f(x) = ax + b (B)
f(x)
= x2 + ax + b
(C) f(x) = (D)
f(x)
= － lnx
8．已知数列{an}的前n项的和 Sn= an － 1（a是不为0的实数），那么{an}
(A) 一定是等差数列 (B)
一定是等比数列
(C) 或者是等差数列，或者是等比数列 (D) 既不可能是等差数列，也不可能是等比数列
二、填空题
9．设A = 
，B =
，则A∩B =_______. (一上17页例6)
10．不等式≥1的解集是_______. (一上43页例5(2))
11．已知A = ，B = ，且A∪B = R，则a的取值范围是________. (一上43页B组2)
12．函数y = 
的定义域是______；值域是______. 函数y =的定义域是______；值域是______. (一上106页A组16)
13．已知数列{an}的通项公式为a n = pn + q，其中p，q是常数，且，那么这个数列是否一定是等差数列？______ 如果是，其首项是______，公差是________. (一上117页116)
14．下列命题中正确的是 。（把正确的题号都写上）
（1）如果已知一个数列的递推公式，那么可以写出这个数列的任何一项；
（2）如果{an}是等差数列，那么{an2}也是等差数列；
（3）任何两个不为0的实数均有等比中项；
（4）已知{an}是等比数列，那么{
}也是等比数列
15．顾客购买一件售价为5000元的商品,如果采取分期付款,那么在一年内将款全部付清的前提下,商店又提出了下表所示的几种付款方案,供顾客选择:
| 方案类别 | 分几次付清 | 付款方法 | 每期所付款额 | 付款总额 | 与一次性付款差额 |
| 1 | 3次 | 购买后4个月第一次付款,再过4个月第二次付款,在过4个月第三次付款 | |||
| 2 | 6次 | 购买后2个月第一次付款,再过2个月第二次付款……购买后12个月第6次付款. | |||
| 3 | 12次 | 购买后1个月第1次付款,过1个月第2次付款……购买后12个月第12次付款. | |||
| 注 | 规定月利率为0.8%,每月利息按复利计算 | ||||
说明:1.分期付款中规定每期所付款额相同.
2.每月利息按复利计算,是指上月利息要计入下月本金. (一上133页研究性学习)
三、解答题
16．如图,有一块半径为R的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.写出这个梯形周长y和腰长x间的函数式,并求出它的定义域.
(一上90页例1)
 |
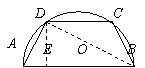17．已知函数y = (x Î R)
(1)求反函数 y = f － 1(x) ;
(2)判断函数y = f － 1(x) 是奇函数还是偶函数. (一上102页例2)
18．已知函数f(x) = loga(a>0, a ≠ 1)。(1)求f(x)的定义域；(2)求使f(x)>0的x取值范围。(一上104页例3)
19．已知Sn是等比数列 {an} 的前项和S3，S9，S6，成等差数列，求证a2，a8，a5成等差数列。(一上132页例4)
20 ．在数列{an}中，a1 = 1，an+1 = 3Sn(n≥1)，求证：a2，a3，┅，an是等比数列。(一上142页B组5)
《回归课本》（一上）
参考答案
DCBC BACC
9. {(1,2)}
10. (－¥,－3]∪(2,5]
11. (1,3)
12. ；(0，1)∪(1， + ¥) 。；[0，1)
13. 是、p + q、p
14. （1）（4）
15. 答案：看课本P134
16. 答案：看课本90页例1
17. 答案：看课本P102例2
18.答案：参看课本P104(应做相应变化)
19. 答案：看课本P132例4
20.略