高三数学《回归课本》(一下)
1、若一个6000的角的终边上有一点P(－4 , a)，则a的值为
(A) 4 (B) －4 (C) ± 4 (D)
2、 =
(A)－ (B) ( C) (D)－
3、= (P38例3)
(A) － (B)
－ (C)
(D)
4、cosa + sina
= (P39例5)
(A) 2sin(+ a ) (B)
2sin(+ a ) (C) 2cos (+ a ) (D)
2cos(－a )
5、tan200 + tan400 + tan200 tan400 = _________。 (P40练习4(1))
6、(1 + tan440)(1 + tan10) = ______；(1 + tan430)(1 + tan20) = ______；(1 + tan420)(1 + tan30) = ______；(1 + tana )(1 + tanb ) = ______ (其中a + b = 45 0)。 (P88A组16)
7、化简sin500(1 + tan100) 。(P43例3)
8、已知tana = ，则sin2a + sin2a = __________。
9、求证(1)1 + cosa =2cos2 ；(2) 1－cosa =2sin2 ；(3) 1 + sina = (sin+cos )2 ；
(4) 1－sina = (sin－cos )2 ；(5) = tan2. (P45例4)(以上结论可直接当公式使用，主要用来进行代数式的配方化简)。
10、cos(p + a ) + cos(p －a )(其中k Î Z) = _________。(P84例1)
11、已知cos(+ x) = ，<x<，求的值。(P91B组10)
12、如图，三个相同的正方形相接，则a +b = .
(P88A组17)
13、已知函数y = 3sin(2x + )，x Î R。
(1) 用五点作图法画出简图；(2) 如何变化可以得到函数y = sinx的图象；(3) 写出其递
减区间；(4) 写出y取得最小值的x的集合；(5)写出不等式3 sin(2x + )>的解集。
(P63例4)
14、已知函数y = Asin(w x + j )，x Î R (其中A>0，w >0)的图象在y轴右侧的第一个最高点(函数取最大值的点)为M(2,2)，与x轴在原点右侧的第一个交点为N(6,0)，求这个函数的解析式。(P84例3)
15、下列各式能否成立？为什么？
(A) cos2x = (B) sinx－cosx = (C) tanx + = 2 (D) sin3x = －
(P89A组25)
16、求函数y = 的定义域。(P91B组12)
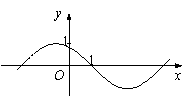
17、如图是周期为2p 的三角函数 y = f (x) 的图象，则 f (x)
可以写成
(A) sin [2 (1－x)] (B) cos (1－x)
(C) sin (x－1) (D)
sin (1－x)
18、与正弦函数
关于直线x = p对称的曲线是
(A)
(B)
(C)
(D)
19、x cos 1－y sin 1＝0的倾斜角是
(A) 1 (B) 1＋ (C) 1－ (D) －1＋
20、函数
在区间[a，b]是减函数，且
，则函数
上
(A)可以取得最大值－A (B)可以取得最小值－A
(C)可以取得最大值A (D)可以取得最小值A
21、已知, 为两个单位向量，下列四个命题中正确的是(P149A组2)
(A) = (B)
如果 与 平行，则 =
(C) · = 1 (D) 2 = 2
22、和向量 = (6,8)共线的单位向量是__________。(P150A组17)
23、已知 = (1,2)， = (－3,2)，当k为何值时，(1)k +与－3垂直？(2) k +与－3平行？平行时它们是同向还是反向？(P147例1)
24、已知 
＝1，
＝
。
（I）若//，求·；
（II）若，的夹角为135°，求 ＋ ．(2004广州一模)
《回归课本》(一下)
参考答案：
1~4、BBDA；
5、；
6、2；
7、1；
8、1；
10、(－1)k (cosa －sina )，k Î Z；
11、－；12、45°；
13、解：(1)
参考课本答案(求周期－列表－描点)；(2)参考课本答案(注意做相应变化)；(3)递减区间是[kp
+ ，kp
+ ]，k
Î Z；(4)
y取得最小值的x的集合是
；(5) 
。
14、y = 2sin(x + )
15、(A) 否 (B) 否 (C) 能 (D) 能
16、(－+ kp, + kp)∪(+ kp, + kp), k Î Z
17~21、DADDD
22、(, ),(－, －)
23、(1)k = 19；(2)k = －，反向。
24、解：（I）∵//，
①若，共向，则 ·＝•＝，
②若，异向，则·＝－•＝－。
（II）∵，的夹角为135°， ∴ ·＝••cos135°＝－1，
∴＋2＝（＋）2 ＝2＋2＋2·＝1＋2－2＝1，
∴
。