高三数学百分能力训练(五)

一、高三数学百分能力训练(五)

二、选择题(5分×8=40分)

1.已知函数f (x)=(2x+5)⁶,导函数f ′(x)中的x³的系数为　　　　　　　　　　  (　　　　)

(A)36000　　(B)24000　　(C)12000　　(D)6000

2.有5个大小相同的球,上面分别标有1,2,3,4,5,现任取两个球,则两个球序号相邻的概率是

(A)　　　 (B)　　　 (C)　　　 (D)　　　　　　　　　　　　　　(　　　　)

3.若函数g(x)=sinx－f (x)在[－,]上单调递增,则的表达式可以是　　　　 (　　　　)

(A)1　　　  (B)cosx　　　(C)－cosx　　 (D)tanx

4.在平面直角坐标系中,O为原点,,P为平面内的动点.若,则P点的轨迹是　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　　　)

(A)圆　　　 (B)椭圆　　　(C)双曲线　　　(D)抛物线

5.不等式xx<x的解集为　　　　　　　　　　　　　　　　　　　　　　　 (　　　　)

(A){x0<x<1}　　(B){ x－1<x<1}　  (C) {x0<x<1或x<－1}　　(D) { x－1<x<0或x>1}

6.二次函数f (x)的二次项系数为正,且对任意实数x,恒有f (2＋x)= f (2－x),若f (1－2x²)< f (1＋2x－x²),则x的取值范围是　　　　　　　　　　　　　　　　　　　　　　 (　　　　)

(A) x>2　　　　(B) x<－2或0<x<2　　　　(C) －2<x<0　　　　(D)无法确定

7.有10级台阶,一次每步跨上一级、二级或三级,共7步走完,则不同的走法总数是(　　　　)

(A)175　　　  (B)42　　　  (C)77　　　  (D)35

8.用一个平面取截正三棱锥及外接球,所得截面如图(图中O为圆心),若球的半径为R,则三棱锥的侧面积等于　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　　　)

O

　　　　　　　　 (A)R²　  (B)R²　  (C)R²　  (D)R².

三、填空题(5分×4=20分)

9.以双曲线两焦点为直径端点的圆与该双曲线有4个交点,这4个交点连同双曲线的两个焦点恰好构成一个正六边形,则此双曲线的离心率为　　　　　　 .

10.某水族馆养了一群热带鱼,这种热带鱼每周死去2条,余下的热带鱼在一周内繁殖后的数量恰为剩下的鱼的数量的2倍,设最初有6条鱼,则第四周后有热带鱼　　　 条.

A F　 E B　　　G　　　C D D

11.如图,在正四面体A-BCD中,E、F、G分别是三角形ADC、ABD、BCD的中心,则△EFG在该正四面体各个面上的射影可能是　　　　　  ,(把所有可能的图的序号均填上)

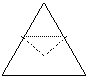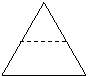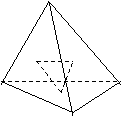
　　　　　　　　　　　　 ①　　　　　　  ②　　　　　　  ③　　　　　　 ④

12.设O是等边三角形ABC的中心,则m＋n=　　　　  .

四、解答题(10分×4=40分)

13.已知△ABC的三个内角A、B、C成等差数列,它们所对的边a ,b ,c满足a＋c=kb,求实数k的取值范围.

14.已知等差数列{a_n}的前n项和为S_n,b_n=,且a₃b₃=,S₃+S₅=21.

(1)　  求{b_n}的通项公式;

(2)　  求证:b₁+b₂+…+b_n<2.

15. 已知函数f (x)=－ .

(1)　  求证:函数y= f (x)的图像关于点(,－)对称;

(2)　  求f (－2) +f (－1)+ f (0)+ f (1)+ f (2)+ f (3)的值.

16.已知定点A(0,－1),B(0,3),C(3,3),以C为焦点作过A,B两点的椭圆,

(1)　  求另一焦点D的轨迹G的方程;

(2)　  过点A的直线l交曲线G于P,Q两点,若,求直线l的方程.

参考答案

一、选择题

1.B  2.B　3.B　4.D  5.C　6.C　7.C  8.B

二、填空题

9.＋1　　10.36　　11.③④　　 12.1

三、解答题

13.∵A、B、C成等差数列, ∴A+C=2B.∴B=60º,

又由余弦定理得b²=a²＋c²－2ac cosB即b²=a²＋c²－2ac cos60º,又由a＋c=kb得a=kb－c,

代入上式得, b²=k²b²－2kbc＋c²＋c²－(kb－c)c,即(k²－1) b²－3kbc＋3 c²=0,

.由⊿≥0得9k²－4×3(k²－1)≥0,∴k²≤4,

解得－2≤k≤2,又a＋c>b,∴kb>b(b>0),∴k>1.于是可得1<k≤2.

14.(1)运用基本量不难得出b _n=;(2)裂项相消法求得T_n=2(1－)<2.

15.(1)证明:

设P(x,y)是y=f (x)的图像上任意一点,它关于(,－)对称点的坐标为(1－x,－1－y),

由已知y=－ ,则－1－y=－1＋=－ ,

∴f (1－x)=－ =－ ,

∴－1－y= f (1－x),即函数y=f (x)的图像关于点(,－)对称.

(2)由(1)有f (1－x)=－1－f (x)即f (x)＋f (1－x)=－1,

∴f (－2) + f (3)=－1, f (－1) + f (2)=－1, f (0) + f (1)=－1,

则f (－2) +f (－1)+ f (0)+ f (1)+ f (2)+ f (3)=－3.

16.(1)由椭圆定义知,∣AC∣＋∣AD∣=∣BC∣＋∣BD∣,

∴∣BD∣－∣AD∣=∣AC∣－∣BC∣.而∣AC∣=5,∣BC∣=3,∴∣BD∣－∣AD∣=2.

则D的轨迹G为双曲线的下支.其中a=1,c=2.∴b=,

轨迹G的方程为(y－1)²－=1(y<1)　　　　　  ①.

(2)设直线l的方程为y=kx－1 …… ②, 将②代入①得,3(kx－2)²－x²－3=0,

即(3k²－1)x²－12kx＋9=0　　　　　　　　　　  ③

设P(x₁,y₁),Q(x₂,y₂),则x₁＋x₂=, x₁x₂=.

∵,∴0－x₁=3(x₂－0),即x₁=－3x₂.消去x₁、x₂得k²=,∴k=.

直线l的方程为y=x－1.