高考系列模拟训练数学试题（一）

高考系列模拟训练数学试题（一）

本试卷分第I卷（选择题）和第Ⅱ卷（非选择题），全卷满分150分，考试时间120分钟。

第I卷（选择题，共60分）

一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．已知向量=（－1，3），=（x，－1），且∥，则等于　（　　）

A．3　　　　　　　　　　　　　　　 B．－　　　　　　　　　 C．　　　　　　　　　　　D．－3

2．将函数y=sinx按向量=（－，3）平移后的函数的解析式为　　　　　　　　　　　　 （　　）

　　　 A．y=sin(x－)+3　　　　　　　　　　　　　　　　　B．y=sin(x－)－3

　　　 C．y=sin(x+)+3　　　　　　　　　　　　　　　　　　D．y=sin(x+)－3　

3．设l、m、n表示三条直线，α、β、γ表示三个平面，则下列命题中不成立的是（　　）

　　　 A．若l⊥α,m⊥α,则l∥m　　　　　　　　　　　

　　　 B．若mβ，n是l在β内的射影，m⊥l，则m⊥n

　　　 C．若mα，nα,m∥n，则n∥α

　　　 D．若α⊥γ，β⊥γ，则α∥β

4．如果数列是首项为1，公比为2的等比数列，

　 那么=　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．2ⁿ⁺¹－1　　　　　　　 B．2ⁿ－1　　　　　　　　　C．2^n－1D．2ⁿ+1

5．已知正六边形ABCDEF，在表达式（1）++（2）2+（3）+中，与相等的有（　　）

A．1个　　　　　　　　　　　　　 B．2个　C．3个　　 D．0个

6．0<x<5是不等式x－2<4成立的　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．充分不必要条件　　　　　　　　　　　　　　　　 B．必要不充分条件

　　　 C．充要条件　　　　　　　　　　　　　　　　　　　　　 D．既不充分也不必要条件

7．已知两直线l₁：y=kx－3，和l₂：x+3y－6=0，设l₁与x轴相交于A点，l₂与y轴相交于C

点，l₁与相l₂交于B点，O为坐标原点，若O、A、B、C四点共圆，则k的值为（　　）

A．3　　　　　　　　　　　　　　　 B．－3　　　　　　　　　　 C．　　　　　　　　　　　D．－

8．直线xsinθ+ycosθ=2+sinθ与圆(x－1)²+y²=4的位置关系是　　　　　　　　　　　　　　　 （　　）

　　　 A．相离　　　　　　　　　 B．相切　　　　　　　　　 C．相交　　　　　　　　　 D．以上都有可能

9．已知x、y满足约束条件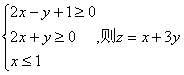的最小值为　　　　　　　　　　 （　　）

　　　 A．7　　　　　　　　　　　　B．　　　　　　　　　　　C．－5　　　　　　　　　　 D．5

10．如图，∠ACB=90°，平面ABC外有一点P，PC=4cm，点P到角的两边AC、BC的距离都等于2cm，那么PC与平面ABC所成角的大小为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．30°　　　　　　　　　 B．45°　　　　　　　　　

　　　 C．60°　　　　　　　　　 D．75°

11．过抛物线y²=4x的焦点的直线交抛物线于A、B两点，

O为坐标原点，则的值是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．12　　　　　　　　　　　B．－12　　　　　　　　　

　　　 C．3　　　　　　　　　　　　D．－3

12．设函数a_n=f（0）+f（）+f（）+…+f（）+f（1）

则a_n= （　）

A．；B．；C．+1；D．+1

第Ⅱ卷（非选择题；共90分）

二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中的横线上.

13．资料表明：有关“非典”的流行病调查发现，地区A新增非典病例人数规律近似于图形f（n）人（如图，n表示第n天，3月3日记为n=0），由于地区A的病原体传染到地区B，导致地区B新增非典病例人数规律近似于f（n－21）人，现有下列判断：

f(n)

①4月23日地区B新增非典病例

100

人数达到100人；

②预测5月9日左右地区B新增非

典病例人数将进入下降趋势；

5.18　n

4.18

4.2

3.3

③预测地区B累计非典病例人数不

会超过4650人

则正确判断有______

14．正方体的全面积是24cm²,它的顶点都在一个球面上，这个球的表面积是　　　　  cm².

15．已知P是椭圆上的一点，F₁、F₂是椭圆的两个焦点，且∠F₁PF₂=60°，则△F₁PF₂的面积是　　　　　　　   .

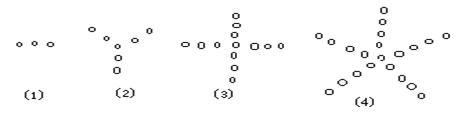
16．沙滩上有一位小朋友用石子拼成下列四个图形，观察图形中相应石子个数的变化规律，试猜测第n个图形中有_______个石子。

三、解答题：本大题6个小题，共74分.解答题应写出文字说明，证明过程或演算步骤.

17．（本小题满分12分）

已知函数

的大小.

18．（本小题满分12分）

　　已知，如图四棱锥P—ABCD中，底面ABCD是平行四边形，PG⊥平面ABCD，垂足为G，G在AD上，且AG=GD，BG⊥GC，GB=GC=2，E是BC的中点，四面体P—BCG的体积为。

（Ⅰ）求异面直线GE与PC所成的角；

（Ⅱ）求点D到平面PBG的距离；

（Ⅲ）若F点是棱PC上一点，且DF⊥GC，求的值。

19．（本小题满分12分）

　　求函数）的最小值，并求其单调区间。

20．（本小题满分12分）

设单调递减函数f（x）的定义域为R，对任意实数x、y∈R，有f（x+y）=f（x）f（y），且当x＜0时，f（x）＞1。

（1）求f（0）；

（2）数列{a_n}满足a₁=f（0），且f（a_n－1）=（n∈N⁺），求通项a_n；

（3）（理）令b_n=，S_n=b₁+b₂+…+b_n，T_n=+…+，试比较S_n与T_n的大小。

21．（本小题满分12分）

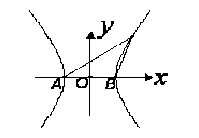　　设双曲线C₁的方程为，A、B为其左、右两个顶点，P是双曲线C₁上的任意一点，引QB⊥PB，QA⊥PA，AQ与BQ交于点Q.

（Ⅰ）求Q点的轨迹方程;

（Ⅱ）设（I）中所求轨迹为C₂，C₁、C₂

的离心率分别为e₁、e₂，当时，e₂的取值范围.

22．（本小题满分14分）

神舟5号飞船返回仓顺利到达地球后，为了及时将航天员安全救出，地面指挥中心在返回仓预计到达区域安排三个救援中心（记为A、B、C），A在B的正东方向，相距6千米，C在B的北偏西30°，相距4千米，P为航天员着陆点，某一时刻，A接受到P的求救信号，由于B、C两地比A距P 远，因此4秒后，B、C两个救援中心才同时接受到这一信号。已知该信号的传播速度为1千米/秒。

（1）求在A处发现P的方位角；

（2）若信号从P点的正上空Q点处发出，则A、B收到信号时间差变大还是变小，说明理由。