高三第一次练习数学试卷
数 学 试 卷（理科）
考试时间：2005年12月
说明：本试卷中所用的符号“
”表示“不含
的自然数的全体”
一、填空题（本大题满分48分，共12题，只要求直接填写结果，每个空格填对得4分，否则一律得零分）
1．不等式
的解集是________________________．
2．设
、
是方程
的两根，则
________________．
3．数列
中的第
项是__________________．
4．集合
非空，则
中所有元素的和是______________．
5．若
（
，且
），则复数
的模是______________．
6．已知函数
的反函数是
，则方程
的解是
_____________________．
7．已知数列
(
)是公差不为零的等差数列，设
，则数列
的前
项
和
的表达式可以是________________________（用中的项表示）．
8．关于函数
有下列命题：① 
的定义域是
；② 是偶函数；③ 在定义域内是增函数；④ 的最大值是
，最小值是．其中正确的命题是______________________（写出你认为正确的所有命题序号）．
9．走廊上有一排照明灯共10盏，为了节约用电，要关掉其中的三盏．如果关掉的三盏灯
不是两端的灯，且任意两盏都不相邻，就不会影响照明，那么随机关掉其中的三盏灯，
影响照明的概率是_________________（用分数表示）．
10．将函数的图像与直线
，
及
轴所围成图形的面积称为函数在
上的面积，已知函数
在
上的面积为
（），则函数
在
上的面积为______________．
11．用锤子以均匀的力敲击铁钉入木板，随着铁钉的深入，铁钉所受的阻力会越来越大，使
得每次钉入木板的钉子长度后一次为前一次的
（
）．已知一个铁钉受击
次后
全部进入木板，且第一次受击后进入木板部分的铁钉长度是钉长的
，请从这个事实
中提炼出一个不等式组：
____________________________________________．
12．已知
，记
（其中
），例如：
，设
，且满足
和
，则有序数组
是________________________．
二、选择题（本大题满分16分，共4题，每题都给出代号为A、B、C、D的四个结论，其
中有全只有一个结论是正确的，必须把正确结论的代号写在题后的圆括号内，选对得4
分，不选、选错或者选出的代号超过一个（不论是否都写在圆括号内），一律得零分）
13．设、
是两个集合，对于
，下列说法正确的是（ ）
A．存在
，使
B．
一定不成立
C．不可能为空集
D．是的充分条件
14．若
，则
一定不属于的区间是（ ）
A．
B．
C．
D．
15．满足不等式
（）的正整数的个数记为
，的前项和记为，则
（ ）
A．
B．
C．
D．
16．已知函数
，则函数
的图像可能是（ ）
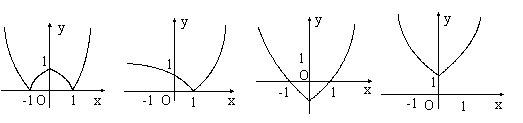
A． B． C． D．
三、解答题（本大题满分86分，共6题，解答下列各题必须写出必要的步骤）
17．（本题满分12分，共2小题，第（1）题9分，第（2）题3分）
设
表示幂函数
在
上是增函数的
的集合，
表示不等式
对任意恒成立的的集合．
（1）求
；
（2）试写出一个解集为的不等式．
18．（本题满分12分，共2小题，第（1）题6分，第（2）题6分）
已知复数
．
（1）当
时，求
的取值范围．
（2）是否存在实数
，使得
，若存在，请求出的值；若不存在，请说明理由；
19．（本题满分14分，共2小题，第（1）题9分，第（2）题5分）
已知
，，关于的一元二次方程
的两实数根
、
满足
，且
，
．
（1）求数列
和
的通项公式； （2）求
的值．
20．（本题满分16分，共2小题，第（1）题4分，第（2）题12分）
已知函数
，
．
（1）在右侧坐标系中作出函数的草图；
（2）研究其值域、奇偶性和单调性，并分别加以证明．
 |
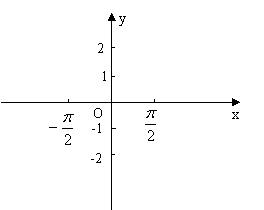21．（本题满分14分，共2小题，第（1）题8分，第（2）题6分）
为了能更好地了解鲸的生活习性，某动物研究所在受伤的鲸身上安装了电子监测装置，从海岸放归点处（如图所示）把它放归大海，并沿海岸线由西到东不停地对鲸进行了
分钟的跟踪观测，每隔
分钟踩点测得数据如下表（设鲸沿海面游动）．然后又在观测站处对鲸进行生活习性的详细观测．已知
，观测站的观测半径为
．
 |
海 岸
| 观测时刻 | 跟踪观测点到放归点 距离 | 鲸位于跟踪观测点正北方向的距离 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
（分钟）
（1）根据表中数据：①计算鲸沿海岸线方向运动的速度；②写出、
满足的关系式并画出鲸的运动路线简图；
（2）若鲸继续以（1）中②的运动路线运动，则鲸大约经过多少分钟（从放归时计时），可进入前方观测站的观测范围（精确到
分钟）？
22．（本题分18分，共3小题，第（1）题4分，第（2）8分，第（3）题6分）
已知函数
，
，为正常数．
（1）可以证明：定理“若
，则
（当且仅当
时取等号）”推广到三个正数时结论是正确的，试写出推广后的结论（无需证明）；
（2）若
在
上恒成立，且函数的最大值大于，求实数的取值范围，并由此猜测
的单调性（无需证明）；
（3）对满足（2）的条件的一个常，设
时，取得最大值．试构造一个定义在
且
，
上的函数
，使当时，
，当
时，取得最大值的自变量的值构成以
为首项的等差数列．