高三第一次月考数学试卷
时间（120分钟）
一．选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1． 若U={1,2,3,4}, M={1,2},N={2,3}, 则
（ ）
(A) {1,2,3} (B) {2} (C) {1,3,4} (D) {4}
2．复数
的值是 （ ）
A．－1 B．1 C．－32 D．32
3．对任意实数
在下列命题中，真命题是 （ ）
A．
是
的必要条件 B．
是
的必要条件
C．是的充分条件 D．是的充分条件
4． 不等式
的解集为 （ ）
A． 
B． 
C． 
D．
5．设函数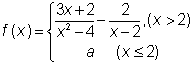
在x=2处连续,则a=
（ ）
A．
B．
C．
D．
6．函数
的反函数是 （ ）
A．y=x2－2x+2(x<1) B．y=x2－2x+2(x≥1)
C．y=x2－2x (x<1) D．y=x2－2x (x≥1)
7．若函数
在区间
上的最大值是最小值的3倍，则
=（ ）
A．
B．
C．
D．
8．已知直线
与曲线
切于点（1，3），则b的值为 （ ）
A．3 B．－3 C．5 D．－5
9．如果奇函数
在区间[3，7]上是增函数，且最小值为5，那么f(x)在[－7，－3]上是（ ）
A．增函数且最小值为－5 B．增函数且最大值为－5
C．减函数且最小值为－5 D．减函数且最大值为－5
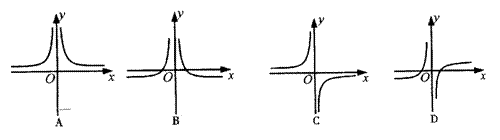10．函数
的图象大致是 （ ）
11．要使函数
上存在反函数，则a的取值范围是 （ ）
A．
B．
C．或 D．
12．定义在R上的函数既是偶函数又是周期函数.若的最小正周期是
，且当
时，
，则
的值为 （ ）
A．
B． C．
D．
二．填空题：本大题共4小题，每小题4分，共16分.答案填在题中横线上.
13．某工厂生产A、B、C三种不同型号的产品，产品数量之比依次为2：3：5。现用分层抽样方法抽出一个容量为
的样本，样本中A种型号产品有16件.那么此样本的容量
.
14．已知复数z满足z=1，则z+1+i的最大值是=__________________.
15．函数
的定义域为__________________.
16．下列函数中，（1）
（2）
(3)
(4) 
其中在
上为增函数的是___________(将所有正确的序号填上)
三:解答题
17．(本题满分12分)
已知复数z1满足(1+i)z1=－1+5i, z2=a－2－i, 其中i为虚数单位,a∈R, 若
<
,求a的取值范围.
18．（本小题满分12分）
一接待中心有A、B、C、D四部热线电话，已知某一时刻电话A、B占线的概率均为0.5，电话C、D占线的概率均为0.4，各部电话是否占线相互之间没有影响.假设该时刻有ξ部电话占线.试求随机变量ξ的概率分布和它的期望.
19．(12分)已知函数y=lg(x2+2x+a)
（1）若函数定义域为R，求a的取值范围；
（2）若函数的值域为R，求a的取值范围.
20．(本题满分12分) 第1小题满分6分, 第2小题满分6分.
记函数f(x)=
的定义域为A, g(x)=lg[(x－a－1)(2a－x)](a<1)
的定义域为B.
(1) 求A；
(2) 若B
A, 求实数a的取值范围.
21．（本小题满分12分）
已知函数
是R上的奇函数，当
时取得极值
.
(1).求的解析式
(2).求单调区间和极大值.
.
22（本题满分14分）
设曲线
≥0）在点M（t,e--t）处的切线
与x轴y轴所围成的三角形面积为S（t）.
（Ⅰ）求切线的方程；
（Ⅱ）求S（t）的最大值.
第一次月考试题答案
一选择题
| 题目 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | A | B | A | C | B | A | A | B | D | C | D |
二、填空题
13、 80 14、 1＋
14、 
15、 （1）、（2）
17．【解】由题意得 z1=
=2+3i,
于是=
=
,=
.
由<,得a2－8a+7<0,
所以 1<a<7.
18．解：P(ξ=0)=0.52×0.62=0.09.
P(ξ=1)=
×0.52×0.62+ ×0.52×0.4×0.6=0.3
P(ξ=2)= 
×0.52×0.62+×0.52×0.4×0.6+ ×0.52×0.42=0.37.
P(ξ=3)= ×0.52×0.4×0.6+×0.52×0.42=0.2
P(ξ=4)= 0.52×0.42=0.04
于是得到随机变量ξ的概率分布列为：
| ξ | 0 | 1 | 2 | 3 | 4 |
| P | 0.09 | 0.3 | 0.37 | 0.2 | 0.04 |
所以Eξ=0×0.09+1×0.3+2×0.37+3×0.2+4×0.04=1.8.
19．【解】（1）因为函数的定义域为R，
所以△=
, 即
（2）由函数的值域为R
则△=
，所以
20．【解】(1)2－
≥0, 得
≥0, x<－1或x≥1
即A=(－∞,－1)∪[1,+ ∞]
(2) 由(x－a－1)(2a－x)>0, 得(x－a－1)(x－2a)<0.
∵a<1,∴a+1>2a, ∴B=(2a,a+1).
∵BA, ∴2a≥1或a+1≤－1, 即a≥或a≤－2, 而a<1,
∴≤a<1或a≤－2, 故当BA时, 实数a的取值范围是(－∞,－2]∪[,1)
21．(1) 解：由奇函数定义，应有
.
即 
因此， 
由条件 
为的极值，必有
故
解得 
(2). 因为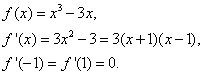 
当 
时，
，故在单调区间
上是增函数.
当 
时，
，故在单调区间
上是减函数.
当 
时，，故在单调区间
上是增函数.
所以，在
处取得极大值，极大值为
22（满分12分）
解：（Ⅰ）因为
所以切线的斜率为
故切线的方程为
即
.
（Ⅱ）令y=0得x=t+1,
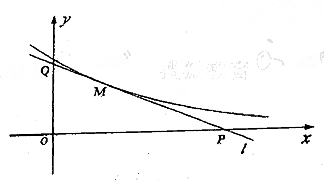又令x=0得
所以S（t）=
=
从而
∵当
（0，1）时，
>0,
当（1,+∞）时,<0,
所以S(t)的最大值为S(1)=