高三第一学期集合、函数、不等式综合练习
一、填空题
1.设集合A={5,log2(a+3)},集合B={a,b}.若A∩B={2},则A∪B= .
2.设集合P={1，2，3，4}，Q={
}，则P∩Q等于
.
3．函数
的反函数是
.
4．已知函数
，则方程
的解
.
5. 已知集合M={xx2<4}，N={xx2-2x-3<0},则集合M∩N= .
6.设奇函数f(x)的定义域为[-5,5].若当x∈[0,5]时, f(x)的图象如右图,
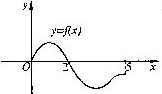则不等式f(x)<0的解是 .
7．方程
的解___ _.
8．函数
的定义域是 .
9.若函数f(x)=a
在[0,+∞)上为增函数,则实数a、b的取值范围是 .
10.已知函数
是奇函数，当
时，
，设
的反函数是
，则
.
11．设A、B为两个集合，下列四个命题：
①A
B
对任意
②AB 
③ABA
B ④AB存在
其中真命题的序号是 .（把符合要求的命题序号都填上）
12．若函数
在区间
上的最大值是最小值的3倍，则
= .
13.若函数
的图象过两点(-1，0)和(0，1)，则a= ,b= .
14．若函数y=f(x)的图象与函数y=lg(x+1)的图象关于直线x-y=0对称,则f(x)= .
15.二次函数y=ax2+bx+c(x∈R)的部分对应值如下表：
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 6 | 0 | -4 | -6 | -6 | -4 | 0 | 6 |
则不等式ax2+bx+c>0的解集是_________.
16．函数
上的最大值和最小值之和为a，则a的值 .
17．设
是函数
的反函数，若
，则
的值为
.
18.设k>1，f(x)=k(x-1)(x∈R) . 在平面直角坐标系xOy中，函数y=f(x)的图象与x轴交于A点，它的反函数y=f -1(x)的图象与y轴交于B点，并且这两个函数的图象交于P点. 已知四边形OAPB的面积是3，则k等于 .
二、选择题
1.设函数
，区间M=[a，b](a<b)，集合N={
}，
则使M=N成立的实数对(a，b)有 ( )
(A)0个 (B)1个 (C)2个 (D)无数多个
2．设集合
对任意实数x恒成立}，则下列关系中成立的是 （ ）
A．P 
Q B．QP C．P=Q D．P
Q=
3．若非空集合
，则“
或
”是“
”的
（ ）
（A）充分非必要条件（B）必要非充分条件（C）充要条件（D）既非充分又非必要条件
4．对于
，给出下列四个不等式 ，
①
; ②
;
③
;
④
其中成立的是 ( )
A．①与③ B．①与④ C．②与③ D．②与④
5．设集合
，
则集合
中元素的个数为
（ ）
A、1 B、2 C、3 D、4
6．一元二次方程
有一个正根和一个负根的充分不必
要条件是： （ ）
A．
B．
C．
D．
7．已知函数
（ ）
A．b
B．-b
C．
D．-
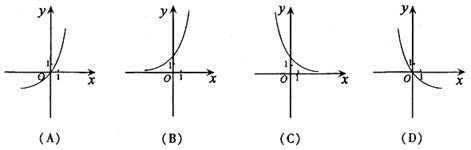
8.已知函数y=log2x的反函数是y=f—1(x)，则函数y= f—1(1－x)的图象是 （ ）
9．设函数
则关于x的方程
解的个数为 （ ）
A．1 B．2 C．3 D．4
10.函数y=-ex的图象 ( )
（A） 与y=ex的图象关于y轴对称. （B） 与y=ex的图象关于坐标原点对称.
（C） 与y=e-x的图象关于y轴对称. （D）与y=e-x的图象关于坐标原点对称.
三．解答题
1.已知f（x）＝2x－1的反函数为
（x），g（x）＝log4（3x＋1）.
(Ⅰ)若f-1（x）≤g（x），求x的取值范围D；
(Ⅱ)设函数H（x）＝g（x）－
（x），当x∈D时，求函数Ｈ（x）的值域.
解：
2.设函数
(为实数).
(Ⅰ)若<0,用函数单调性定义证明:
在
上是增函数;
(Ⅱ)若=0,
的图象与的图象关于直线
对称,
求函数的解析式.
解：
3.已知函数
，
（
为正常数），且函数
与
的
图象在
轴上的截距相等。（1）求的值； （2）求函数
的单调递增区间；
（3）若
为正整数，证明：
.（可不做）
解：
4.已知函数
(
，
为实常数)
(I) 若＝2，b＝-1，求
的值域．
(II) 若的值域为[0，＋∞)，求常数，b应满足的条件．
解:
5. 已知集合A＝{x êx2+(a-1)x-a＞0}，B＝{x ê(x+a)(x+b)＞0}，其中a≠b，M＝{x êx2-2x-3≤0}，全集为R．(1)若
＝M，求a、b的值；
(2)若a＞b＞-1，求A∩B；
(3)若a2+
∈
，求a的取值范围．
解：
6.已知二次函数
满足条件：
=
，且方程=
有等根。(Ⅰ)求的解析式；(Ⅱ)是否存在实数m、n(m<n)，使的定义域和值域分别是[m，n]和[3m，3n]?如果存在，求出m、n的值；若不存在，说明理由。
.解:
集合、函数、不等式综合练习解答
一、填空题
1.设集合A={5,log2(a+3)},集合B={a,b}.若A∩B={2},则A∪B= {1,2,5} .
2.设集合P={1，2，3，4}，Q={}，则P∩Q等于 {1，2} .
3．函数的反函数是
.
4．已知函数，则方程的解____1____.
5. 已知集合M={xx2<4}，N={xx2-2x-3<0},则集合M∩N= {x-1<x<2} .
6.设奇函数f(x)的定义域为[-5,5].若当x∈[0,5]时, f(x)的图象如右图,则不等式f(x)<0的解是 (－2,0)∪(2,5] .
7．方程的解____2___.
8．函数的定义域是 
.
9.若函数f(x)=a在[0,+∞)上为增函数,则实数a、b的取值范围是a>0且b≤0 .
10.已知函数是奇函数，当时，，设的反函数是，则 -2 .
11．设A、B为两个集合，下列四个命题：
①AB对任意 ②AB
③ABAB ④AB存在
其中真命题的序号是 4 .（把符合要求的命题序号都填上）
12．若函数在区间上的最大值是最小值的3倍，则=
.
13.若函数的图象过两点(-1，0)和(0，1)，则a= 2 ,b=
2 .
14．若函数y=f(x)的图象与函数y=lg(x+1)的图象关于直线x-y=0对称,则f(x)= 10x-1.
15.二次函数y=ax2+bx+c(x∈R)的部分对应值如下表：
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 6 | 0 | -4 | -6 | -6 | -4 | 0 | 6 |
则不等式ax2+bx+c>0的解集是_____
或
____.
16．函数上的最大值和最小值之和为a，则a的值
.
17．设是函数的反函数，若，则
的值为
2 .
18.设k>1，f(x)=k(x-1)(x∈R) . 在平面直角坐标系xOy中，函数y=f(x)的图象与x轴交于A点，它的反函数y=f
-1(x)的图象与y轴交于B点，并且这两个函数的图象交于P点. 已知四边形OAPB的面积是3，则k等于 
.
二、选择题
1.设函数，区间M=[a，b](a<b)，集合N={}，
则使M=N成立的实数对(a，b)有 ( A )
(A)0个 (B)1个 (C)2个 (D)无数多个
2．设集合对任意实数x恒成立}，则下列关系中成立的是 （ A ）
A．P Q B．QP C．P=Q D．PQ=
3．若非空集合，则“或”是“”的
（ B ）
（A）充分非必要条件（B）必要非充分条件（C）充要条件（D）既非充分又非必要条件
4．对于，给出下列四个不等式 ，
①; ②;
③;
④
其中成立的是 ( D )
A．①与③ B．①与④ C．②与③ D．②与④
5．设集合，则集合中元素的个数为
（ B ）
A、1 B、2 C、3 D、4
6．一元二次方程有一个正根和一个负根的充分不必
要条件是： （ C ）
A．
B．
C． D．
7．已知函数 （ B ）
A．b
B．-b
C．
D．-
8.已知函数y=log2x的反函数是y=f—1(x)，则函数y= f—1(1－x)的图象是 （ B ）
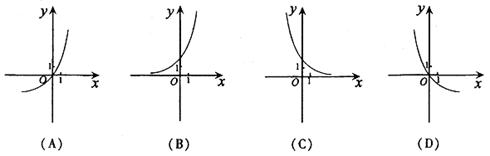
9．设函数
则关于x的方程解的个数为 （ C ）
A．1 B．2 C．3 D．4
10.函数y=-ex的图象 ( D )
A 与y=ex的图象关于y轴对称. B 与y=ex的图象关于坐标原点对称.
C 与y=e-x的图象关于y轴对称. D 与y=e-x的图象关于坐标原点对称.
三．解答题
1.已知f（x）＝2x－1的反函数为（x），g（x）＝log4（3x＋1）.
(Ⅰ)若f-1（x）≤g（x），求x的取值范围D；
(Ⅱ)设函数H（x）＝g（x）－
（x），当x∈D时，求函数Ｈ（x）的值域.
解：(Ⅰ)∵
∴
(x＞-1) 2分
由
≤g（x） ∴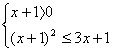
4分 解得0≤x≤1 ∴D＝［0，1］ 6分
(Ⅱ)H（x）＝g（x）－
9分
∵0≤x≤1 ∴1≤3－
≤2 ∴0≤H（x）≤ ∴H（x）的值域为［0，］12分
2.设函数(为实数).
(Ⅰ)若<0,用函数单调性定义证明:在上是增函数;
(Ⅱ)若=0,的图象与的图象关于直线对称,
求函数的解析式.
3.已知函数，（为正常数），且
函数与的图象在轴上的截距相等。
（1）求的值；
（2）求函数的单调递增区间；
（3）若为正整数，证明：.
解：(1)由题意，
，
又
，所以
。
(2)
当
时，
，它在
上单调递增；
当
时，
，它在
上单调递增。
(3)设
，考查数列
的变化规律：
解不等式
，由
，上式化为
解得
，因
得
，于是
，而
所以
。
………………12分
4.已知函数 (，为实常数)
(I) 若＝2，b＝-1，求的值域．
(II) 若的值域为[0，＋∞)，求常数，b应满足的条件．
解:(I) ∵ x2＋2x－1＝(x－1)2－2≥－2，∴
≥0,
∴ f(x)的值域为[2，+∞)．
(II)当a＝0时，则须x2＋b的最小值≤0，∴b≤0 ;
当a≠0时，只须a＜0，且x2＋ax＋b＝
的最小值
＝a2，
即4b＝5a2. ∴ a＝0，b≤0或a＜0，4b＝5a2 .
5. 已知集合A＝{x êx2＋(a－1)x－a＞0}，B＝{x ê(x＋a)(x＋b)＞0}，其中a≠b，M＝{x êx2－2x－3≤0}，全集R．
(1)若＝M，求a、b的值；(2)若a＞b＞－1，求A∩B；
(3)若a2＋
∈，求a的取值范围．
(1)解：A＝{x ê(x－1)(x＋a)＞0}，M＝{x ê－1≤x≤3} ………2分
＝{x｜(x＋a)(x＋b)≤0}
…………3分
若＝M，则a＝1，b＝－3或a＝－3，b＝1．…………………………5分
(2)解：∵a＞b＞－1 ，∴－a＜－b＜1
故A＝{x êx＜－a或x＞1}，B＝{x êx＜－a或x＞－b} ………… 7分
因此A∩B＝{x êx＜－a或x＞1}．…………………………………………8分
(3) ＝{x ê(x－1)(x＋a)≤0}，
由a2＋
∈ 得：(a2－
)( a2＋＋a)≤0，…………………………10分
解得：
或
，
∴a的取值范围是{x｜或}．…………………… 12分
6.已知二次函数满足条件：=，且方程=有等根。
(Ⅰ)求的解析式；(Ⅱ)是否存在实数m、n(m<n)，使的定义域和值域分别是
[m，n]和[3m，3n]?如果存在，求出m、n的值；若不存在，说明理由。
.解: (1)由条件易得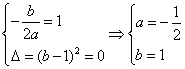
,∴
……6分
(2)假设存在这样的m、n满足条件,由于
所以3n≤即n≤<1,故二次函数f (x)在区间[m,n]上是增函数,从而有
…………………………12分