当前位置：首页 -高中数学试卷 - 高中三年级数学试题 - 正文*

高考数学仿真试题(三)

2014-5-11 0:20:11下载本试卷

高考数学仿真试题(三)

 

本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟.

第Ⅰ卷　(选择题　共60分)

一、　选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）　

1.不等式(1+x)(1-x)＞0的解集是

A.{x-1＜x＜1｝　　　　　　　　　　　　 B.{xx＜1｝

C.{xx＜-1或x＞1＝　　　　　　　　　　 D.{xx＜1且x≠-1＝

2.对一切实数x，不等式x2+ax+1≥0恒成立，则实数a的取值范围是

A.（-∞，-2）　　　　　　　　　　　　　 B.［-2，+∞)　

C.［-2，2］　　　　 　　　　　　　　　　D.［0，+∞)

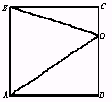3.设O为矩形ABCD的边CD上一点，以直线CD为旋转轴，旋转这个矩形所得体积为V，其中以OA为母线的圆锥体积为，则以OB为母线的圆锥的体积等于

A. 　　　　　　　　　　　　　　　B.

C. 　　　　　　　　　　　　　　　D.

4.设偶函数f(x)=logax-b在（-∞，0）上递增，则f(a+1)与f(b+2)的大小关系是

A.f(a+1)=f(b+2)　　　　　　　　　　 B.f(a+1)＞f(b+2)

C.f(a+1)＜f(b+2)　　　　　　　　　　D.不确定

5.复数z1、z2在复平面上对应点分别是A、B，O为坐标原点，若z1=2(cos60°+isin

60°)z2，z2=2，则△AOB的面积为

A.4　　　　　　　B.2　　　　　　　　　C.　　　　　　　 D.2

6.如果二项式（）n的展开式中第8项是含的项，则自然数n的值为

A.27　　　　　　　　B.28　　　　　　　　　　C.29　　　　　　　　D.30

7.A、B、C、D、E，5个人站成一排，A与B不相邻且A不在两端的概率为

A.　　　　　　　 B.　　　　　　　　　　C.　　　　　　　 D.以上全不对

8.把函数y=cosx-sinx的图象向左平移m个单位（m＞0）所得的图象关于y轴对称，则m的最小值是

A.　　　　　　　　B. 　　　　　　　 C. 　　　　　　 D.

9.已知抛物线C1：y=2x2与抛物线C2关于直线y=-x对称，则C2的准线方程是

A.x=-　　　　　　 B.x=　　　　　　　C.x=　　　　　　　D.x=-

10.6人一个小组，其甲为组长，乙为副组长，从6人中任选4人排成一排，若当正、副组长都入选时，组长必须排在副组长的左边（可以不相邻），则所有不同排法种数是

A.288　　　　　　　 B.276　　　　　　　 C.252　　　　　　　 D.72

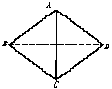11.如图△ABD≌△CBD，则△ABD为等腰三角形，∠BAD=∠BCD=90°，且面ABD⊥面BCD，则下列4个结论中，正确结论的序号是

①AC⊥BD　②△ACD是等边三角形　③AB与面BCD成60°角　④AB与CD成60°角

A.①②③　　　　　　　　　　　　　　　　B.①②④

C.①③④　　　　　　　　　　　　　　　　D.②③④

12.台风中心从A地以每小时20千米的速度向东北方向移动，离台风中心30千米内的地区为危险区，城市B在A的正东40千米处，B城市处于危险区内的时间为

A.0.5小时　　　　　 B.1小时　　　　　　 C.1.5小时　　　　　 D.2小时

第Ⅱ卷　(非选择题　共90分)

二、填空题（本大题共4小题，每小题4分，共16分.把答案填在题中横线上）　

13.在△ABC中，cos(B+C)+cos(+A)的取值范围是　　　　　  .

14.函数f(x)= (x≠-1)，若它的反函数是f-1(x)= ,则a=　　　　.

15.Sn是等差数列{an}的前n项和，a5=2，an-4=30(n≥5,n∈N)，Sn=336,则n的值是　　　.

16.给出四个命题：①两条异面直线m、n，若m∥平面α，则n∥平面α　②若平面α∥平面β，直线mα，则m∥β　③平面α⊥平面β，α∩β=m，若直线m⊥直线n，nβ，则n⊥α　④直线n平面α，直线m平面β，若n∥β，m∥α，则α∥β，其中正确的命题是　　　　　  .

三、解答题（本大题共6小题，共74分解答应写出文字说明、证明过程或演算步骤） 17.（本小题满分12分）　　

解关于x的方程：loga(x2-x-2)=loga(x-)+1(a＞0且a≠1).

18.（本小题满分12分）　　

已知等差数列{an}中，a2=8，S10=185.　

（Ⅰ）求数列{an}的通项公式an;

（Ⅱ）若从数列{an}中依次取出第2，4，8，…，2n，…项，按原来的顺序排成一个新数列{bn}，试求{bn}的前n项和An.　

19.（本小题满分12分）　　

在Rt△ABC中，∠ACB=30°，∠B=90°，D为AC中点，E为BD的中点，AE的延长线交BC于F，将△ABD沿BD折起，二面角A—BD—C大小记为θ.　

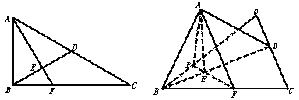
（Ⅰ）求证：面AEF⊥面BCD；　

（Ⅱ）θ为何值时，AB⊥CD.　

20.（本小题满分12分）　　

某公司取消福利分房和公费医疗，实行年薪制工资结构改革，该公司从2000年起每人的工资由三个项目并按下表规定实施　

项目

金额（元/人·年）

性质与计算方法

基础工资

一万元

考虑物价因素，从2000年起每年递增10%（与工龄无关）

房屋补贴

400元

按照职工到公司的年限计算，每年递增400元

医疗费

1600元

固定不变

如果公司现有5名职工，计划从明年起每年新招5名职工　

（Ⅰ）若今年（2000年）算第一年，试把第n年该公司付给职工工资总额y(万元)表示成年限n的函数；　

（Ⅱ）试判断公司每年发给职工工资总额中，房屋补贴和医疗费的总和能否超过基础工资总额的20%？

21.（本小题满分12分）　　

设双曲线C的中心在原点，以抛物线y2=2x-4的顶点为双曲线的右焦点，抛物线的准线为双曲线的右准线.

（Ⅰ）试求双曲线C的方程；　

（Ⅱ）设直线l:y=2x+1与双曲线C交于A、B两点，求AB；　

（Ⅲ）对于直线y=kx+1,是否存在这样的实数k，使直线l与双曲线C的交点A、B关于直线y=ax(a为常数)对称，若存在，求出k值；若不存在，请说明理由.

　22.（本小题满分14分）　　

已知函数f(x)=ax2+bx+c(a＞b＞c)的图象上有两点A（m，f(m1)）、B(m2，f(m2))，满足f(1)=0且a2+(f(m1)+f(m2))·a+f(m1)·f(m2)=0.

（Ⅰ）求证：b≥0；

（Ⅱ）求证：f(x)的图象被x轴所截得的线段长的取值范围是［2，3)；　

（Ⅲ）问能否得出f(m1+3)、f(m2+3)中至少有一个为正数？请证明你的结论.

2004年高考数学仿真试题(三)答案

一、1.D　2.B  3.A　4.B　5.B  6.C　7.D　8.C9.C　10.A　11.B　12.B

二、13.［-2,］　14. 1　15. 21　16.②③

三、17.解：原方程可化为loga(x2-x-2)=loga(ax-2)　　　　　　　　　　　　　　　　　　　 2分

①

②
 
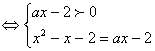　　　　　　　　　　　  　　　　　　　　　　　　　　　 4分

由②得x=a+1或x=0,当x=0时，原方程无意义，舍去.　　　　　　　　　　　　　　　 8分

当x=a+1由①得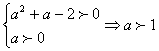　　　　　  　　　　　　　　　　　　　 10分

∴a＞1时，原方程的解为x=a+1　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 12分

18.解：(Ⅰ)设{an}首项为a1,公差为d,

则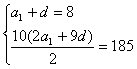,解得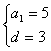

∴an=5+3(n-1),即an=3n+2　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 6分

（Ⅱ）设b1=a2,b2=a4,b3=a8,

则bn=a2n=3×2n+2

∴An=(3×2+2)+(3×22+2)+…+(3×2n+2)

=3×(2+22+…+2n)+2n

=3×+2n=6×2n-6+2n　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 12分

19.（Ⅰ）证明：在Rt△ABC中，∠C=30°，D为AC的中点，则△ABD是等边三角形

又E是BD的中点，∵BD⊥AE，BD⊥EF，

折起后，AE∩EF=E，∴BD⊥面AEF

∵BD面BCD，∴面AEF⊥面BCD　　　　　　　　　　　　　　　　　　　　　　　　　　　　6分

（Ⅱ）解：过A作AP⊥面BCD于P，则P在FE的延长线上，设BP与CD相交于Q，令AB=1，则△ABD是边长为1的等边三角形，若AB⊥CD，则BQ⊥CD,又AE=

∴折后有cosAEP=

由于∠AEF=θ就是二面角A—BD—C的平面角，

∴当θ＝π-arccos时，AB⊥CD　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 12分

20.解：（Ⅰ）第n年共有5n个职工，那么基础工资总额为5n(1+)n（万元）

医疗费总额为5n×0.16万元，房屋补贴为

5×0.04+5×0.04×2+5×0.04×3+…+5×0.04×n=0.1×n(n+1)（万元）　　　　　　2分

∴y=5n(1+)n+0.1×n(n+1)+0.8n

=n［5(1+)n+0.1(n+1)+0.8］（万元）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　6分

（Ⅱ）5(1+)n×20%-［0.1(n+1)+0.8］

=(1+)n-(n+9)

=［10(1+)n-(n+9)］

∵10(1+)n=10(1+Cn1Cn1+Cn2+…)

＞10(1+)＞10+n＞n+9

故房屋补贴和医疗费总和不会超过基础工资总额的20%　　　　　　　　　　　　　　　　　 12分

21.解：（Ⅰ）由抛物线y2=2x-4,即y2=2 (x-),可知抛物线顶点为（,0）,准线方程为x=.

在双曲线C中，中心在原点，右焦点（，0），右准线x=,

∴

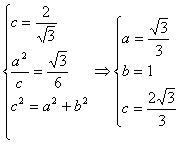
∴双曲线c的方程3x2-y2=1　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　 4分

（Ⅱ）由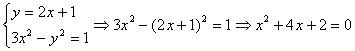

∴AB=2　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　8分

（Ⅲ）假设存在实数k,使A、B关于直线y=ax对称，设A(x1,y1)、B(x2,y2),

②

③
 
则

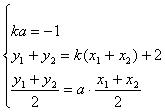
由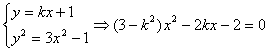　　　　  ④

由②③，有a(x1+x2)=k(x1+x2)+2　　　　　　　　　　　 ⑤

由④知：x1+x2=代入⑤

整理得ak=3与①矛盾，故不存在实数k，使A、B关于直线y=ax对称.　　　 12分

22.（Ⅰ）证明：因f(m1),f(m2)满足a2+［f(m1)+f(m2)］a+f(m1)f(m2)=0

即［a+f(m1)］［a+f(m2)］=0

∴f(m1)=-a或f(m2)=-a,

∴m1或m2是f(x)=-a的一个实根，

∴Δ≥0即b2≥4a(a+c).

∵f(1)=0,∴a+b+c=0

且a＞b＞c,∴a＞0,c＜0,

∴3a-c＞0,∴b≥0　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　 5分

(Ⅱ)证明：设f(x)=ax2+bx+c=0两根为x1,x2,则一个根为1，另一根为,

又∵a＞0,c＜0，

∴＜0,

∵a＞b＞c且b=-a-c≥0,

∴a＞-a-c＞c,∴-2＜≤-1

2≤x1-x2＜3　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 10分

（Ⅲ）解：设f(x)=a(x-x1)(x-x2)=a(x-1)(x-)

由已知f(m1)=-a或f(m2)=-a

不妨设f(m1)=-a则a(m1-1)(m1-)=-a＜0,

∴＜m1＜1

∴m1+3＞+3＞1

∴f(m1+3)＞f(1)＞0

∴f(m1+3)＞0　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 12分

同理当f(m2)=-a时，有f(m2+3)＞0,

∴f(m2+3)或f(m1+3)中至少有一个为正数　　　　　　　　　　　　　　　　　　　　　　　　　　　　 14分