高三摸底统一考试数学试题
说明:1、本试卷分第I卷(选择题)和第II卷(非选择题),满分150分,考试时间120分钟.
2、注明理科的题,理科生作,注明文科的题,文科生作,未注明的题都作.
第I卷(选择题,共60分)
一、选择题(每小题5分,共60分)
1、已知![]()
![]() ,
,![]() =
=![]() ,全集
,全集![]() =R,则
=R,则![]()
![]() =( )
=( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
2、不等式![]() 的解集是( )
的解集是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3、下列函数中,图象与函数![]() 的图象关于
的图象关于![]() 轴对称的是( )
轴对称的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4、函数![]() 是( )
是( )
A、周期为![]() 的奇函数
B、周期为
的奇函数
B、周期为![]() 的偶函数
的偶函数
C、周期为2![]() 的奇函数
D、周期为2
的奇函数
D、周期为2![]() 的偶函数
的偶函数
5、给定映射![]() ,
,![]() ,则点(
,则点(![]() ,
,![]() )的原象是( )
)的原象是( )
A、(![]() ,
,![]() )
B、(
)
B、(![]() ,
,![]() )
)
C、(![]() ,
,![]() )或(
)或(![]() ,
,![]() ) D、无原象
) D、无原象
6、已知函数![]() ,则它的单调区间是( )
,则它的单调区间是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
7、某人的密码是一种五位数字号码,每位上的数字可在0到9这10个数字选取,开箱时,随意按下一个五位数字号码,正好按对密码的概率是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
8、已知直线![]()
![]() 和平面
和平面![]() ,那么
,那么![]() 的一个必要但非充分条件是( )
的一个必要但非充分条件是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
![]()
9、若![]() ,
,![]() ,则
,则![]() 的平分线上的向量
的平分线上的向量![]() 是( )
是( )
A、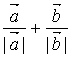 B、
B、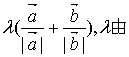
![]() 决定
决定
C、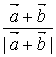 D、
D、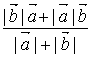
10、已知数列![]() 是各项均为正数的等比数列,比值
是各项均为正数的等比数列,比值![]() ,那么( )
,那么( )
A、![]() B、
B、![]()
C、![]() D、大小不确定
D、大小不确定
11、函数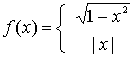
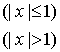 ,若方程
,若方程![]() 有且只有一个实根,那么
有且只有一个实根,那么![]() 满足( )
满足( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
12、(理)已知![]() ,则
,则![]() 的值是( )
的值是( )
A、0 B、4 C、-4 D、不确定
12、(文)已知函数![]() 的值域为R,则实数
的值域为R,则实数![]() 的取值范围是( )
的取值范围是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
第II卷(非选择题,共90分)
二、填空(每小题4分,共16分)
13、(理)若![]() ,
,![]() 是纯虚数,则
是纯虚数,则![]() 的值为_______________
的值为_______________
13、(文)已知![]()
![]() 满足约束条件
满足约束条件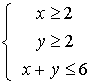 ,则
,则![]() 的取值范围是____
的取值范围是____
14、设![]() ,则
,则![]() ___
___
15、设P、Q是两个非空集合,定义![]() ,若
,若![]() 3,4,5
3,4,5![]() ,
,![]() 4,5,6,7
4,5,6,7![]() ,则
,则![]() 中元素个数有___________个
中元素个数有___________个
16、若不等式![]() 在
在![]() 内恒成立,则
内恒成立,则![]() 的取值范围是_______
的取值范围是_______
三、解答题(6个小题,共74分)
17、(12分)△ABC中,![]() 、
、![]() 、
、![]() 分别是∠A、∠B、∠C的对边,已知tanA+tanB+
分别是∠A、∠B、∠C的对边,已知tanA+tanB+![]() =
=![]() tanAtanB.
tanAtanB.
①求∠C的大小;
②若![]() =
=![]() ,△ABC面积
,△ABC面积![]() ,求
,求![]() 的值.
的值.
18、(12分)有甲、乙两批种子,发芽率分别为0.8、0.7,从两批种子中各取1粒,求:
①2粒种子都能发芽的概率;
②至少有1粒种子发芽的概率;
③恰好有1粒种子发芽的概率.
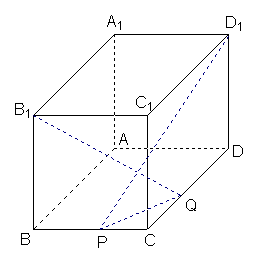 19、(12分)已知正方体ABCD-A
19、(12分)已知正方体ABCD-A![]() B
B![]() C
C![]() D
D![]() 的棱长为2,P、Q分别是BC、CD上的动点, PQ =
的棱长为2,P、Q分别是BC、CD上的动点, PQ =![]() .
.
①确定P、Q的位置,使B![]() Q⊥D
Q⊥D![]() P;
P;
②当B![]() Q⊥D
Q⊥D![]() P时,求二面角C
P时,求二面角C![]() - PQ-A的大小.
- PQ-A的大小.
20、(12分,理)设函数![]() ,
,![]() (
(![]() ).
).
①若![]() 在
在![]() 是增函数,求
是增函数,求![]() 的取值范围;
的取值范围;
②求![]() 在
在![]() 上的最大值.
上的最大值.
20、(12分,文)已知![]() .
.
① 若![]() 在
在![]() 上单调递增,求
上单调递增,求![]() 的取值范围;
的取值范围;
② 是否存在实数![]() ,使
,使![]() 在
在![]() 上单调递减?若存在,求
上单调递减?若存在,求![]() 的范围,若不存在,说明理由.
的范围,若不存在,说明理由.
21、(13分)已知定点F(1,0),动点P在![]() 轴上运动,过点P作PM交
轴上运动,过点P作PM交![]() 轴于点M,并延长MP到点N,且
轴于点M,并延长MP到点N,且![]() ,
,![]() .
.
① 求动点N的轨迹方程;
② 直线![]() 与动点N的轨迹交于A、B两点,若
与动点N的轨迹交于A、B两点,若![]() ,且
,且![]() AB
AB![]() ,求直线
,求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
22、(13分)由坐标原点O向曲线![]() (
(![]() )引切线,切于O以外的点P
)引切线,切于O以外的点P![]() (
(![]() ,
,![]() ),再由P
),再由P![]() 引曲线的切线,切于P
引曲线的切线,切于P![]() 以外的点P
以外的点P![]() (
(![]() ,
,![]() ),如此进行下去,得到点列P
),如此进行下去,得到点列P![]() (
(![]() ,
,![]() ).
).
① 求![]() 与
与![]() (
(![]() )的关系式;
)的关系式;
②(文)若![]() ,证明
,证明![]() 为等比数列,并求
为等比数列,并求![]() .
.
②(理)当![]() ,求P
,求P![]() 的极限位置的坐标.
的极限位置的坐标.