高三年级第四次阶段考试数学试题
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,有且只有一个选项正确.
1.已知![]() ,则
,则![]() ( )
( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2.在![]() 中,条件甲:
中,条件甲:![]() ;条件乙:
;条件乙:![]() ,那么甲是乙的( )
,那么甲是乙的( )
![]() 充分非必要条件
充分非必要条件 ![]() 必要非充分条件
必要非充分条件 ![]() 充要条件
充要条件 ![]() 非充分非必要条件
非充分非必要条件
3.在坐标平面内,与点![]() 的距离是1,且与点
的距离是1,且与点![]() 的距离为2的直线共有( )
的距离为2的直线共有( )
![]() 1条
1条
![]() 2条
2条
![]() 3条
3条
![]() 4条
4条
4.已知![]() ,则
,则![]() 有( )
有( )
![]() 最大值
最大值![]()
![]() 最小值
最小值![]()
![]() 最大值1
最大值1 ![]() 最小值1
最小值1
5.已知数列![]() 中,
中,![]() ,能使
,能使![]() 的
的![]() 的数值是( )
的数值是( ) ![]() 14
14 ![]() 15
15 ![]() 16
16 ![]() 17
17
6.在圆![]() 内一点
内一点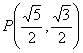 有
有![]() 条弦,这
条弦,这![]() 条弦的长度成等差数列
条弦的长度成等差数列![]() ,若过点
,若过点![]() 的圆的最短的弦长为数列的首项
的圆的最短的弦长为数列的首项![]() ,最长的弦长为为
,最长的弦长为为![]() ,若公差
,若公差![]() ,则
,则![]() 的取值集合为( )
的取值集合为( )
![]() {5,6,7}
{5,6,7} ![]() {4,5,6}
{4,5,6} ![]() {3,4,5}
{3,4,5} ![]() {3,4,5,6}
{3,4,5,6}
7.函数![]() 满足
满足![]() ,且
,且![]() ,则
,则![]() =
=
![]()
![]()
![]()
![]()
8.函数![]() ,则
,则![]() 的大小关系为( )
的大小关系为( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
9.设![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 与过焦点的直线交于
与过焦点的直线交于![]() 、
、![]() 两点,则
两点,则![]() ( )
( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
10.设![]() 时,不等式
时,不等式![]() 恒成立,则
恒成立,则![]() 的取值范围是( )
的取值范围是( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
11.若椭圆经过原点,且焦点![]() ,则其离心率为( )
,则其离心率为( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
12.![]() 的顶点为
的顶点为![]() 、
、![]() ,
,![]() 的内切圆的圆心在直线
的内切圆的圆心在直线![]() 上,则顶点
上,则顶点![]() 的轨迹方程是( )
的轨迹方程是( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
二、填空题:本大题共6小题,每小题4分,共24分,把答案填在第二卷相应的横线上。
13.在![]() 和
和![]() 之间插入三个数,使这三个数成等比数列,则插入的这三个数的乘积为 。
之间插入三个数,使这三个数成等比数列,则插入的这三个数的乘积为 。
14.若![]() ,则
,则![]() 在
在![]() 方向上的投影为
。
方向上的投影为
。
15.要用一块边长为![]() 的正方形铁板四角各剪去一个小正方形,再把四边折起焊成一个无盖水箱,当四角正方形边长
的正方形铁板四角各剪去一个小正方形,再把四边折起焊成一个无盖水箱,当四角正方形边长![]() 时,水箱的容积最大。
时,水箱的容积最大。
16.设函数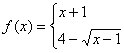
![]() ,则使
,则使![]() 的自变量
的自变量![]() 的范围是
。
的范围是
。
17.设![]() 满足约束条件
满足约束条件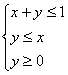 ,则
,则![]() 的最大值为
。
的最大值为
。
18.已知圆方程为![]() ,动抛物线过点
,动抛物线过点![]() 且以圆的切线为准线,则抛物线的焦点的轨迹方程为
。
且以圆的切线为准线,则抛物线的焦点的轨迹方程为
。
三、解答题:本大题共5小题,共66分,19-20小题满分12分,21-23小题满分14分,解答应写出必要的文字说明、证明过程或演算步骤
19.已知向量![]() (
(![]() 为常数),若向量
为常数),若向量![]() 与
与![]() 的夹角
的夹角![]() 为锐角,求实数
为锐角,求实数![]() 的取值范围。
的取值范围。
20.已知数列![]() 是各项为不同的正数的等差数列,
是各项为不同的正数的等差数列,![]() 、
、![]() 、
、![]() 成等差数列,又
成等差数列,又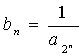 (
(![]() )。
)。
(1)证明:![]() 为等比数列;
为等比数列;
(2)若数列![]() 的前3项的和为
的前3项的和为![]() ,求数列
,求数列![]() 的首项
的首项![]() 和公差
和公差![]() 。
。
21.设计某高速公路时,要求最低车速为![]() ,最小车距为
,最小车距为![]() (
(![]() 为定值),并且车速
为定值),并且车速![]() 与车距
与车距![]() 之间必须满足关系:
之间必须满足关系:![]() 。
。
(1)求常数![]() 的值;
的值;
(2)求这条高速公路上的一条车道上每小时的最高车流量(单位时间车流量=![]() )。
)。
22.已知双曲线![]() 的方程为
的方程为![]() ,过右焦点
,过右焦点![]() 作双曲线在第一、三象限的渐近线的垂线
作双曲线在第一、三象限的渐近线的垂线![]() ,垂足为
,垂足为![]() ,
,![]() 与双曲线
与双曲线![]() 的左、右支交点分别为
的左、右支交点分别为![]() 、
、![]() 。
。
(1)求证:点![]() 在双曲线
在双曲线![]() 的右准线上;
的右准线上;
(2)求双曲线![]() 的离心率
的离心率![]() 的取值范围;
的取值范围;
(3)若![]() ,求离心率
,求离心率![]() 。
。
23.已知定义在实数集![]() 上奇函数
上奇函数![]() 有最小正周期2,且当
有最小正周期2,且当![]() 时,
时,![]() 。
。
(1)求函数![]() 在
在![]() 上的解析式;
上的解析式;
(2)证明:函数![]() 在
在![]() 上是减函数;
上是减函数;
(3)当![]() 为何值时,方程
为何值时,方程![]() 在
在![]() 上有实数解。
上有实数解。