高三年级数学第一次调研考试

　　　　　　　　　　　　　　　　　　 

第一部分选择题 （共60分）

参考公式：

如果事件A、B互斥，那么　　　　　　　　　　　　　　球的表面积公式

P（A+B）=P（A）+P（B）　　　　　　　　  其中R表示球的半径

如果事件A、B相互独立，那么　　　　　　　　　　 球的体积公式

P（A·B）=P（A）·P（B）　　　　　　　　　　　　　　　　 其中R表示球的半径

如果事件A在一次试验中发生的概率是P.　 那么n次独立重复试验中恰好发生k次的

概率

一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.

（1）函数的反函数是

(A) 　　　(B) 　　　(C) 　　　(D)

（2）在正四面体ABCD中，BC所在直线与AD所在直线所成角是

(A) 30⁰　　　(B)45⁰　　　 (C)60⁰　　　 (D)90⁰

（3）设曲线在点M处切线斜率为3，则点M的坐标为

(A)（0，－2）　　　 (B)（1，0）　　　 (C)（0，0）　　　 (D)（1，1）

（4）函数是

(A) 周期为的奇函数　　　　(B) 周期为的偶函数　　　

(C) 周期为2的奇函数　　  (D) 周期为2的偶函数

（5）棱长为1的正方体的八个顶点都在同一个球的表面上，则这个球的表面积为

(A)2　　　 (B) 3　  (C)　　　 (D) 12

（6）在区间上递增的函数是

(A)　　(B) 　　(C) 　　(D)

（7）将函数的图象按向量平移后所得图象的解析式是

(A) 　　　 (B) 　　　

(C) 　　　　　　 (D)

（8）条件，条件，若p是q的充分不必要条件，则a的取值范围是

(A) 　　　(B) 　　　(C) 　　　(D)

（9）已知曲线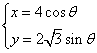上一点P到点A（－2，0）、点B（2，0）的距离之差为2，则△PAB是

(A)锐角三角形　　　 (B) 直角三角形　　　(C)钝角三角形　　　 (D) 等腰三角形

（10）已知过点P（－2，2）且垂直于向量＝（3，4）的直线与圆相切，则实数a的值为

(A) 4　　　(B) 　　　 (C) 4或　　  (D) －1或

（11）已知集合，则集合A中元素个数为

(A) 16　　　(B)14　　　 (C)9　　　 (D)8

（12）设数列的前n项和为，令，称为数列，，……，的“理想数”，已知数列，，……，的“理想数”为2004，那么数列2， ，，……，的“理想数”为

(A) 2002　　 (B) 2004　　　(C) 2006　　　(D) 2008

高三年级第一次调研考试

数　 学

第二部分 非选择题　（共90分）

二、填空题（本大题每小题4分，共16分。）

（13）已知向量，，若，则m的值是　　 .

（14）在条件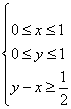下，则的最大值是　　　　 .

（15）设有两个命题：①关于x的不等式的解集是R，②函数是减函数.如果这两个命题中有且只有一个真命题，则实数m的取值范围是　　　　　　  .

（16）已知数列满足＝24，且，那么＝　　　　 .

三、解答题：（本大题共6小题，共74分）

（17）（本小题满分12分）

已知向量，.

（Ⅰ）当⊥时，求＋的值；

（Ⅱ）求函数＝·（－）的值域.

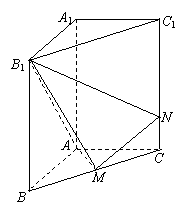
（18）（本小题满分12分）

如图，在直三棱柱ABC－A₁B₁C₁中，AA₁＝2，AB＝AC＝1，∠BAC＝90⁰，已知点M是BC的中点，点N在侧棱CC₁上.

（Ⅰ）当线段CN的长度为多少时，MN⊥AB₁；

（Ⅱ）若MN⊥AB₁，求B₁N与平面AB₁M所成角的余弦值.

（19）（本小题满分12分）

箱内有大小相同的6个白球，4个黑球，从中任意取出1个，记录它的颜色后再放回箱内，搅拌后再任意取出1个，记录它的颜色后又放回箱内搅拌，假设这样的抽取共进行了3次，试回答下列问题：

（Ⅰ）求事件A：“第一次取出黑球，第二次取出白球，第三次取出黑球”的概率；

（Ⅱ）若取出1只白球得2分，取出1只黑球得1分，求三次取球的总得分的数学期望.

（20）（本小题满分12分）

设数列的前n项和为，数列的前n项和为，已知，.

（Ⅰ）求数列的通项公式；

（Ⅱ）是否存在一个最小正整数M，当时，恒成立？若存在，求出这个M的值；若不存在，请说明理由.

（21）（本小题满分12分）

已知点A（0，1），x、y∈R，m≥2，设，为直角坐标平面内x，y轴正方向上的单位向量，若向量，，且.

（Ⅰ）求动点M（x，y）的轨迹方程，并指出方程所表示的曲线；

（Ⅱ）设直线l：与点M的轨迹交于B、C两点，问是否存在实数m使得？若存在，求出m的值；若不存在，试说明理由.

（22）（本小题满分14分）

已知函数，当点M（x，y）在的图象上运动时，点N（）在函数的图象上运动.

（Ⅰ）求的解析式；

（Ⅱ）若函数的极小值为4，求函数的单调区间；

（Ⅲ）若在时，恒成立，求参数a的取值范围.

高三年级第一次调研考试

数学试题参考答案及评分标准

一、　选择题

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	C	D	B	A	B	C	A	C	B	C	B	A

二、  填空题

（13）　　 （14）3　　 （15）m＝0或m≥1　　 （16）2004

三、  解答题

（17）（Ⅰ）；　（Ⅱ）.

（18）（Ⅰ）CN＝时，MN⊥AB₁；　（Ⅱ）.

（19）（Ⅰ）；　（Ⅱ）E＝4.8.

（20）（Ⅰ）；　（Ⅱ）存在M＝4.

（21）（Ⅰ）当m＝2时，点M的轨迹是一条射线，方程为：y＝0（x≥2）；

当m＞2时，点M的轨迹是双曲线的右支，方程为：（x≥2）.

（Ⅱ）满足条件的m不存在.

（22）（Ⅰ）.

（Ⅱ）的单调递增区间为，单调递减区间为.

（Ⅲ）.