高三年级数学试题2
班级 学号 姓名
一、选择题：（本大题共12小题，每小题5分，共60分。）
1、若直线
与圆
相切，则a的值为
A、1，—1 B、2，—2 C、1 D、—1
2、已知m、n为异面直线，m平面
，n平面
，∩=l，则l
A、与m、n都相交 B、与m、n中至少一条相交
C、与m、n都不相交 D、至多与m、n中的一条相交
3、不等式
的解集是
A、{x0≤x<1} B、{xx<0且x≠—1}
C、{x—1<x<1} D、{xx<1且x≠—1}
4、函数
在[0，1]上的最大值与最小值的和为3，则a的值为
A、
B、2 C、4
D、
5、在（0，2
）内，使
成立的x取值范围为
A、
B、
C、
D、∪
6、设集合M=
，N=
，则
A、M=N B、M N C、N M
D、M∩N=
7、椭圆5x2+ky2=5的一个焦点是（0，2），则k等于
A、—1
B、1 C、
D、
8、正六棱柱ABCDEF—A1B1C1D1E1F1的底面边长为1，侧棱长为
，则这个棱柱的侧面对角线E1D与BC1所成的角是
A、900 B、600 C、450 D、300
9、函数y=x2+bx+c (x∈[0, +∞)) 是单调函数的充要条件是
A、b≥0 B、b≤0 C、b>0 D、b<0
10、已知0<x<y<a<1，则有
A、log a (xy)<0 B、0<log a (xy)<1
C、1<log a (xy)<2 D、log a (xy)>2
11、从正方体的6个面中选取3个面，其中有2个面不相邻的选法共有
A、8种 B、12种 C、16种 D、20种
12、平面直角坐标系中，O为坐标原点，已知两点A（3，1），B（—1，3），若点C满足OC = OA + OB，其中、∈R，且+=1，则点C的轨迹方程为
A、(x—1)2 + (y—2)2 =5 B、3x+2y—11=0
C、2x—y=0 D、x+2y—5=0
二、填空题：（本大题共4小题，每小题4分，共16分）
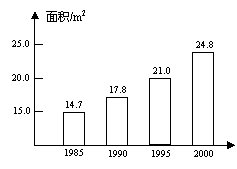13、据新华社2002年3月12日电，
1985年到2000年间，我国农村人均居
住面积如图所示，其中从 年到
年的五年间增长最快。
14、已知
（
，
则cot=
。
15、甲、乙两种冬小麦试验品种连续5年
平均单位面积产量如下（单位：吨/公顷）
| 品种 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 |
| 甲 | 9.8 | 9.9 | 10.1 | 10 | 10.2 |
| 乙 | 9.4 | 10.3 | 10.8 | 9.7 | 9.8 |
其中产量比较稳定的小麦品种是 。
16、设函数f(x)在（—∞，+∞）内有定义，下列函数：
（1）y= —f(x) ； （2）y=xf(x2) ；
（3）y= —f(—x) ； （4）y=f(x)—f(—x)
其中必为奇函数的有 。
选择题答题表：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
三、解答题：（本大题共6小题，共74分）
17、（本小题满分12分）
在等比数列{an}中，已知a6—a4=24，a3a5=64，求{an}的前8项和S8
18、（本小题满分12分）
已知
，
，求
、
的值。
19、（本小题满分12分）
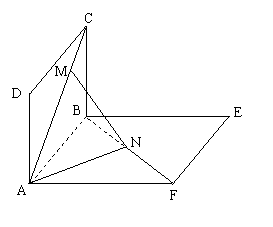
如图，正方形ABCD、ABEF的边长都是1，而且平面ABCD、ABEF互相垂直，点M在AC上移动，点N在BF上移动，若CM=BN=a（0<a<），
（1）求MN的长；
（2）当a为何值时，MN的长最小；
（3）当MN长最小时，求面MNA与MNB所成二面角的大小。
 |
20、（本小题满分12分）
某单位6个员工借助互联网开展工作，每个员工上网的概率都是0.5（相互独立），
（1）求至少3人同时上网的概率；
（2）至少几个人同时上网的概率小于0.3 ？
21、（本小题满分12分）
已知a>0，函数f(x)=x3—a，x∈[0，+∞），设x1>0，记曲线y=f(x)在点M（x1，f(x1)）处的切线为l，
（1）求l的方程；
（2）设l与x轴交点为（x2，0）
证明：①x2≥
②若
，则
22、（本小题满分14分）
已知两点M（—1，0），N（1，0），且点使MP·MN，PM·PN，NM·NP成公差小于零的等差数列。
（1）点P的轨迹是什么曲线？
（2）若点P的坐标为（x0，y0），
为PM与PN的夹角，求tan。