试卷类型：A

高三年级数学统考试题

 (理工农医类)

本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．第Ⅰ卷1至2页，第Ⅱ卷3至8页，共150分，考试用时120分钟．

第 Ⅰ 卷 (选择题，共60分)

注意事项：

1．请考生将自己的学校、班级、姓名、学号填写在第Ⅱ卷密封线内．

2．每小题选出答案后用2B铅笔把答题卡上对应题目的答案代号涂黑，如需改动，必须用橡皮擦干净后，再选涂其它答案，不能答在试题卷上．

3．考试结束后，监考人员将本试卷和答题卡一并收回．

参考公式：

正棱台、圆台侧面积公式： 其中、c分别表示上、下底面周长，l表示斜高或母线长 台体体积公式：

如果事件A、B互斥，那么 P(A＋B)＝P(A)＋P(B) 如果事件A、B相互独立，那么 P(A · B)＝P(A) · P(B) 如果事件A在一次试验中发生的概率是p，那么n次独立重复试验中恰好发生k次的概率

一．选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1.　　m＝－2是直线(2－m)x＋my＋3＝0和直线x－my－3＝0互相垂直的
　　A．充分不必要条件　　　　　　　　　　　　　　　　　　B．必要不充分条件
　　C．充要条件　　　　　　　　　　　　　　　　　　　　　　　 D．既不充分又不必要条件

2.　　设复数z₁＝(a²＋3)＋(－4a－3)i，z₂＝(a－7)＋(a²＋a)i ，且z₁＋z₂＝2＋i，则实数a的值为
　　A．－3　　　　　　　　　　　B．2　　　　　　　　　　　　　C．1　　　　　　　　　　　　　D．不存在

3.　　一动圆圆心在抛物线x²＝4y上，过点(0，1)且恒与定直线l相切，则直线l的方程为
　　A．x＝l　　　　　　　　　　　B．x＝　　　　　　　　 C．y＝－1　　　　　　　　 D．y＝

4.　　若椭圆(a＞b＞0)的离心率为，则双曲线的离心率为
　　A．　　　　　　　　　　　 B．　　　　　　　　　　C．　　　　　　　　　　　 D．

5.　　不等式≤x－1的解集是
　　A．(－∞，－1]∪[3，+∞)　　　　　　　　　　　　　B．[－1，1)∪[3，+∞)
　　C．[－1，3]　　　　　　　　　　　　　　　　　　　　　　　　D．(－∞，－3)∪[1，+∞)

6.　　函数f (x)＝x²－2 ln x的单调递减区间是
　　A．(0，1]　　　　　　　　　　　　　　　　　　　　　　　　　 B．(－∞，－1] 、(0，1]
　　C．[－1，1]　　　　　　　　　　　　　　　　　　　　　　　　D．[1，+∞)

7.　　设曲线和曲线在它们交点处的两切线的夹角为，则tan＝
　　A．1　　　　　　　　　　　　　B．　　　　　　　　　　　 C．　　　　　　　　　　　 D．

8.　　若函数对任意的实数都有，则＝
　　A．0　　　　　　　　　　　　　B．1　　　　　　　　　　　　　C．－1　　　　　　　　　　　D．1或－1

9.　　 奇函数y＝f (x) (x∈R)有反函数y＝f ^－1 (x)，则必在y＝f ^－1 (x)的图象上的点是
　　A．(－f (a)，－a)　　　B．(－f (a)，a)　　　　　C．(－a， f ^－1 (a))　　D．(a， f ^－1 (－a))

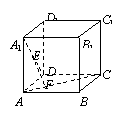
10. 如图，在正方体ABCD—A₁B₁C₁D₁中，EF是异面直线AC与A₁D的公垂线，则由正方体的八个顶点所连接的直线中，与EF平行的直线
　　A．有且仅有一条　　　 B．有二条
　　C．有四条　　　　　　　　 D．不存在

11. 从集合｛1，2，3，…，10｝中任意选出三个不同的数，使这三个数成等比数列，这样的等比数列个数为
　　A．3　　　　　　　　　　　　　B．4　　　　　　　　　　　　　C．6　　　　　　　　　　　　　D．8

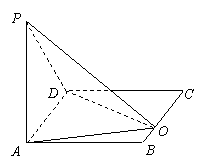
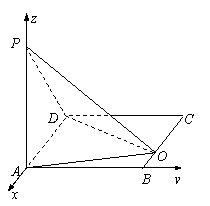
12. 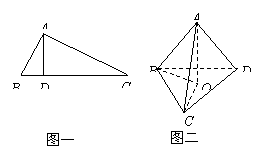如图一，在△ABC中，AB⊥AC、AD⊥BC，D是垂足，则（射影定理）。类似有命题：三棱锥A－BCD (图二)中，AD⊥平面ABC，AO⊥平面BCD，O为垂足，且O在△BCD内，则，上述命题是
　　A．真命题
　　B．假命题
　　C．增加“AB⊥AC”的条件才是真命题
　　D．增加“三棱锥A－BCD是正三棱锥”的条件才是真命题

高三年级统考试题

数  学(理工农医类)

第 Ⅱ 卷 (非选择题，共90分)

注意事项：

第Ⅱ卷共6页，用黑色签字笔直接答在试题卷中，答卷前将密封线内的项目填写清楚．

题 号	一	二	三						总　 分
			17	18	19	20	21	22
得 分

得分	评卷人

二．填空题：本大题共4小题，每小题4分，共16分。将正确答案填在题中横线上．

13. 等比数列{a_n}中，T_n表示前n项的积，若T₅＝1，则a₃＝　　　　　　　　．

14. 已知x、y满足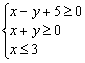： ，则z＝x＋2y的最大值是　　　　　　 .

15. 某保险公司新开设了一项保险业务，规定该份保单在一年内如果事件E发生，则该公司要赔偿a元，假若在一年内E发生的概率为p，为使公司受益的期望值不低于a的，公司应要求该份保单的顾客缴纳的保险金最少为_________________元．

16. 规定记号“”表示一种运算，即R^*．若，则函数的值域是　　　　　　　　　．

三．解答题：本大题共6小题，满分74分．

得分	评卷人

17.　 (本大题满分12分)已知向量a＝(cosx，sinx)，b＝()，且x∈[0，]．若f (x)＝a · b－2｜a＋b｜的最小值是，求的值．

得分	评卷人

18.　 (本大题满分12分)在袋里装30个小球，其中彩球中有n (n≥2)个红色、5个蓝色、10个黄色，其余为白球．若从袋里取出3个都是相同颜色彩球(无白色)的概率是，求红球的个数，并求从袋中任取3个小球至少有一个是红球的概率．

19.　 (本大题满分12分)数列{a_n}是等比数列，a₁＝1，公比q是的展开式中的第二项(按x的降幂排列)．
　　(1)求数列{a_n}的通项a_n与前n项和S_n；
　　(2)若，求A_n．

得分	评卷人

20.　 (本大题满分12分) 如图，在矩形ABCD中，AB＝，BC＝a，又PA⊥平面ABCD，PA＝4．
　　(1)若在边BC上存在一点Q，使PQ⊥QD，求a的取值范围；
　　(2)当BC上存在唯一点Q，使PQ⊥QD时，求异面直线AQ与PD所成角的大小；
　　(3)若a＝4，且PQ⊥QD，求二面角A－PD－Q的大小．

得分	评卷人

21.　 (本大题满分12分) 已知a＞0，函数，x∈[0，+∞)，设x₁＞0，记曲线y＝f (x)在点M (x₁，f (x₁))处的切线为l．
　　(1)求l的方程；
　　(2)设l与x轴交点为(x₂，0)，证明：①x₂≥，②若，则．

得分	评卷人

22.　 (本大题满分14分)设、y∈R，i、j为直角坐标平面内、轴正方向上的单位向量，向量a＝xi＋(y＋2)j，b＝xi＋(y－2)j ，且 a ＋ b ＝8．
　　(1)求点M (x，y)的轨迹C的方程；
　　(2)过点(0，3)作直线与曲线C交于A、B两点，设，是否存在这样的直线，使得四边形OAPB是矩形？若存在，求出直线的方程；若不存在，试说明理由．

得分	评卷人

襄樊市高三年级统考试题

数学参考答案及评分标准(理工农医类)

一．选择题：ADCBB　 ACDAA　 DA

二．填空题：13．1　　14．19　　15．(p＋0.1)a 　16．(1，+∞)

三．解答题：

17．解：a · b　　　　　　　　　　　　　　　　　　　　2分
　　 a＋b 　　　 4分
　　　∴cos x≥0，因此 a＋b ＝2 cos x
　　∴f (x)＝a · b－2｜a＋b｜即　　　　　　　　　　　　　　　　　　6分
　　　∴0≤cos x≤1
　　①若＜0，则当且仅当cos x＝0时，f (x)取得最小值－1，这与已知矛盾；　　　　 8分
　　②若0≤≤1，则当且仅当cos x＝时，f (x)取得最小值，
　　由已知得，解得：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 10分
　　③若＞1，则当且仅当cos x＝1时，f (x)取得最小值，
　　由已知得，解得：，这与相矛盾．
　　综上所述，为所求．　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　12分

18．解：取3个球的方法数为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　2分
　　设“3个球全红色”为事件A，“3个全蓝色”为事件B，“3个球全黄色”为事件C，则
　　，　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 4分
　　∵A、B、C为互斥事件　∴P(A＋B＋C)= P(A)＋P(B)＋P(C)
　　即  Þ  P(A)＝0　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 6分
　　∴红球的个数≤2，又∵n≥2，故n ＝2　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　8分

记“3个球中至少有一个是红球”为事件D，则为“3个球中没有红球”
　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 12分

19．(1)解：∵ 的第二项为，∴q＝x　　　　　　　　　　　　 2分
　　∴a_n＝x^n－1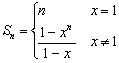，　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 6分

(2)解：当x＝1时，
　　又
　　∴，A_n＝n · 2 ^n－1　　　　　　　　　　　　　　　　　　　　8分
　　当x≠1时，
　　　　　　　　　　　　　10分
　　
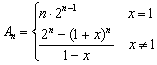　　∴　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 12分

20．方法一
　　(1)解：以为x、y、z轴建立空间直角坐标系，则
　　B(0，，0)，C(－a，，0)，D(－a，0，0)，P(0，0，4)　　　　　　　　　　　　　　  2分
　　设Q(t，，0)，则
　　＝(t，，－4)，＝(t＋a，，0)
　　∵PQ⊥QD，∴＝0
　　即t²＋at＋3＝0　　①
　　∴△＝a²－12≥0　Þ　a≥2．　　 4分

(2)解：∵BC上存在唯一点Q，使PQ⊥QD，
　　∴△＝a²－12＝0　Þ　a＝2，t＝－　　　　　　　　　　　　　　　  6分
　　＝(－，，0) ，＝(－2，0，－4)
　　∴cos
　　故异面直线AQ与PD所成角为arccos．　　　　　　　　　　　　　　 8分

(3)解：过Q作QM∥CD交AD于M，则QM⊥AD，M(t，0，0)
　　∵PA⊥平面ABCD，∴PA⊥QM，又QM⊥AD，∴QM⊥平面PAD
　　过M作MN⊥PD于N，连结NQ，由三垂线定理知QN⊥PD
　　∴∠MNQ是二面角A－PD－Q的平面角
　　设N (m，0，n)，则＝(t－m，0，－n)，＝(t－m，，－n)
　　＝(－4－m，0，－n)
　　∵MN⊥PD，ND、PD共线，∴
　　得：m＋n－t＝0，m－n＝4　　②
　　
　　由①得：t＝－1或t＝－3，由②得：n＝2＋t
　　当t＝－1时，，当t＝－3时，
　　∴二面角A－PD－Q的大小为或．　　　　　　　　  12分

方法二

(1)解：设BQ＝t，则PQ²＝19＋t²，QD²＝3＋(a－t)²，PD²＝16＋a²
　　由PQ⊥QD得：19＋t²＋3＋(a－t)²＝16＋a²，即t²－at＋3＝0　　①
　　∴△＝a²－12≥0　Þ　a≥2．　　　　　　　　　  　　　　　　　　　 4分

(2)解：∵BC上存在唯一点Q，使PQ⊥QD，
　　∴△＝a²－12＝0　Þ　a＝2，t＝，故Q是BC中点
　　取AD中点R，PA中点S，连RS、RC，则RS∥PD，RC∥AQ
　　∴∠RSC就是异面直线AQ与PD所成角　　　　　　　　　　　　　　　　 6分
　　，，
　　∴
　　故异面直线AQ与PD所成角为arccos．　　　　　　　　　　　　　  8分

(3)解：同方法一得∠MNQ是二面角A－PD－Q的平面角　　　　　　　　  10分
　　在Rt△PAD中，
　　在Rt△PQD中，
　　
　　由①得t＝1或t＝3
　　当t＝1时，，当t＝3时，
　　∴二面角A－PD－Q的大小为或．　　　　　　　  12分

21．(1)解：，∴曲线y＝f (x)在点M (x₁，f (x₁))处的切线的斜率
　　∴切线l的方程为，即　　　　　　　　　　　4分

(2)解：令y＝0得
　　①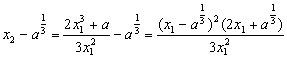≥0　　(*)
　　∴，当且仅当时等号成立．　　　　　　　　　　　　　　　　　　　　　　　　　　　　　6分

②∵，∴(*)中“＝”不成立，故　　　　　　　　　　　　　　　　　　　　　　　　　 8分
　　
　　∵　∴，故x₂＜x₁
　　∴当时，成立．　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　12分

22．(1)解：∵a＝xi＋(y＋2)j，b＝xi＋(y－2)j ，且 a ＋ b ＝8
　　∴点M(x，y)到两个定点F₁(0，－2)，F₂(0，2)的距离之和为8　　　　　　　　　　　　　　　2分

　　∴轨迹C为以F₁，F₂为焦点的椭圆，方程为　　　　　　　　　　　　　　　　　　 4分

 (2)解：过轴上的点(0，3)，若直线是轴，则A、B两点是椭圆的顶点
　　∴0，∴P与O重合，与四边形OAPB是矩形矛盾．　　　　　　　　 6分
　　∴直线的斜率存在，设方程为y＝kx＋3，A(x₁，y₁)，B (x₂，y₂)
　　由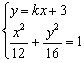 得：　　　　　　　　　　　　　　　　　　　　　　　　　 8分
　　此时，恒成立，
　  且　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 10分
　  ∵，∴四边形OAPB是平行四边形
　　若存在直线，使得四边形OAPB是矩形，则OA⊥OB，即0
 　 ∴　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　12分
　  即　Þ　
　　解得：
　　∴存在直线l：，使得四边形OAPB是矩形．　　　　　　　　　　　　　　　　14分