高三年级一月调考数学试题
本试卷分第I卷（选择题）和第II卷（非选择题）两部分。共150分。考试时间120分钟。
第I卷（选择题 共60分）
参考公式：
如果事件A、B互斥，那么P（A+B）=P（A）+P（B）
如果事件A、B相互独立，那么P（A·B）=P（A）·P（B）
如果事件A在一次试验中发生的概率是P，那么n次独立重复试验中恰好发生k次的概率
Pn（k）=C
Pk（1－P）n－k
球的表面积公式S=4πR2 其中R表示球的半径
球的体积公式V=
πR3 其中R表示球的半径
|
1．如果全集
（ UB）等于 （ ）
A．
B．（2，4）
C．
D．
2．已知数列{
}是等差数列，且
等于 （ ）
A．1 B．4 C．5 D．6
3．（文科）锐角
的值为 （ ）
A．
B．
C．
D．
（理科）复数
等于 （ ）
A．
B．
C．
D．
4．不等式
的解集为 （ ）
A．
B．
C．
D．
5．已知函数
的图象过（1，0），则
的反函数的图象一定过点（ ）
A．（1，2） B．（2，1） C．（0，2） D．（2，0）
6．从P点引三条射线PA，PB，PC，每两条射线夹角为60°，则平面PAB和平面PBC所成二面角正弦值为 （ ）
A．
B．
C．
D．
7．（文科）点（1，a）到直线
值为 （ ）
A．2 B．
C．
D．－
（理科）已知两点A（3，2）和B（－1，4）到直线
距离相等，则m值为
（ ）
A．
B．
C．
D．
8．设
是两个非零向量，且
共线，则实数k值为（ ）
A．
B．－ C．
D．8
9．若双曲线
的渐近线l方程为
，则双曲线焦点F到渐近线l的距离为（ ）
A．2 B．
C．
D．2
10．6个人站成前后二排，每排三人，其中甲不站前排，乙不站在后排的站法种数为（ ）
A．72 B．216 C．360 D．108
11．已知x，y满足不等式组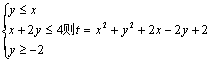
的最小值为 （ ）
A．
B．2 C．3 D．
|
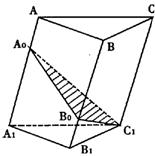
AA1，BB1上的点，且知BB0:B0B1=3:2，过A0，B0，C1
的截面将三棱柱分成上下两个部分体积之比为2:1，则
AA0:A0A1= （ ）
A．2:3 B．4:3
C．3:2 D．1:1
第II卷（非选择题，共90分）
二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上.
13．
.
14．某气象站天气预报准确率是80%，5次预报中至少有4次准确的概率是
（精确到0.01）.
15．（文科）
系数为
.
（理科）
.
16．下列四个命题
①分别和两条异面直线均相交的两条直线一定是异面直线.
②一个平面内任意一点到另一个平面之距离均相等，那么这两个平面平行.
③一个二面角的两个半平面分别垂直于另一个二面角的两个半平面，则这两个二面角的平面角相等或互补.
④过两异面直线外一点能作且只能作出一条直线和这两条异面直线同时相交.
其中正确命题的编号是 .
三、解答题：本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤.
17．（本小题满分12分）
（文科）在等比数列{}中，已知
.
（1）求
（2）求
.
（理科）若锐角
（1）
； （2）
18．（本小题满分12分）文科做（1）（2），理科做（1），（3）
|
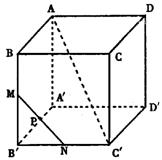
线，M、N分别为BB′，B′C′中点，P为线段MN中点.
（1）求DP和平面ABCD所成的角的正切；
（2）求四面体P－AC′D′的体积；
（3）求DP和AC′所成角.
19．（本小题满分12分）
（文科）要制造一种机器零件，甲机床废品率为0.05，而乙机床废品率为0.1，而它们
的生产是独立的，从它们制造的产品中，分别任意抽取一件，求：
（1）其中至少有一件废品的概率；
（2）其中至多有一件废品的概率.
（理科）甲乙两人独立解某一道数学题，已知该题被甲独立解出的概率为0.6，被甲或乙解出的概率为0.92.
（1）求该题被乙独立解出的概率；
（2）求解出该题的人数
的数学期望和方差.
20．（本小题满分12分）
（文科）若锐角
：
（1）； （2）.
（理科）数列{}满足递推式
（1）求a1，a2，a3；
（2）若存在一个实数
，使得
为等差数列，求值;
（3）求数列{}的前n项之和.
21．（本小题满分12分）文科做（1）（2） 理科做（1）（3）
函数
（1）若
的表达式；
（2）在（1）的条件下，求
上最大值；
（3）若函数
上单调递增，求b的取值范围.
22．（本小题满分14分）
（文科）已知椭圆C的中心在原点，焦点在x轴上，一条经过点
且方向向量为
的直线l通过椭圆C的右焦点F，且交椭圆C于A、B两点，又
（1）求直线l的方程； （2）求椭圆C的方程.
（理科）已知椭圆C的中心在原点，焦点在x轴上，一条经过点（3，－）且方向向量为的直线l交椭圆C于A、B两点，交x轴于M点，又
.
（1）求直线l方程； （2）求椭圆C长轴长取值的范围.
参考答案
一、选择题：每小题5分，共60分
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | C | 文C 理B | D | A | A | 文C 理B | C | C | B | B | A |
二、填空题，每小题4分，共16分
13．
14．0.74; 15．（文）20；（理）a=1或-2; 16．②
三、解答题（共74分）
17．（本小题满分12分）
（文）解：
（理）解：（1）
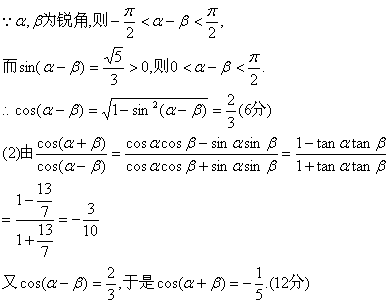
18．（本小题满分12分）
解：（1）过P作PH⊥BC于足H，连DH，
∵面BC′⊥面AC，则PH⊥面ABCD，
∴DP和面ABCD所成角即为∠HDP.
在正方形BCC′B′，M，N分别为BB′，B′C′中点，P为MN中点，
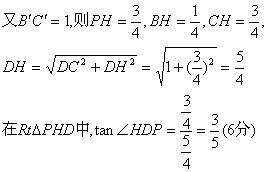
（2）连BC′和B′C交于Q，因为BCC′B′为正方形，则PQ⊥BC′
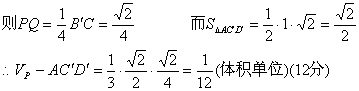
（3）延长BC至E，延长
至F，
使CE=C′F=1，连DF，则DF//AC′
∴异面直线AC′和DP所成角转化为求
∠PDF，连PF
|
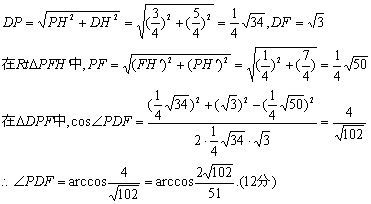
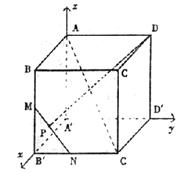
或解：建立如图空间直角坐标系
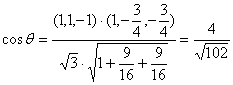
19．（本小题满分12分）
（文）解：设事件A=“从甲机床抽得的一件是废品”；
B=“从乙机床抽得的一件是废品”.
则P（A）=0.05, P(B)=0.1,
（1）至少有一件废品的概率
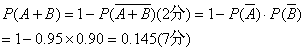
（2）至多有一件废品的概率
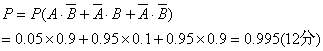
（理）解：（1）记甲、乙分别解出此题的事件记为A、B.
设甲独立解出此题的概率为P1，乙为P2.（2分）
则P（A）=P1=0.6,P(B)=P2
|
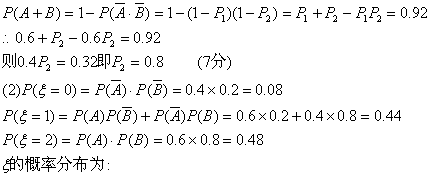
| 0 | 1 | 2 |
| P | 0.08 | 0.44 | 0.48 |
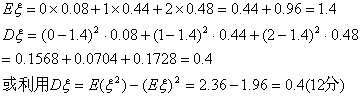
20．（本小题满分12分）
（文）解：（1）
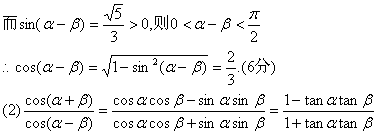
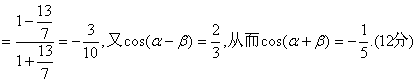
（理）解：（1）由
同理求得a2=23, a1=5 （4分）
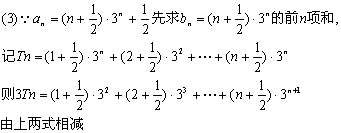
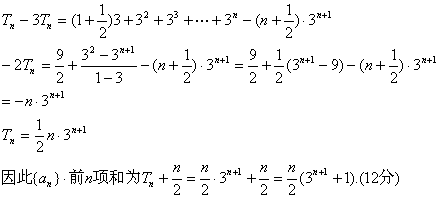
21．（本小题满分12分）
解：（1）
（2）
| x |
| －2 |
|
|
|
|
| + | 0 | － | 0 | + |
|
|
| 极大 |
| 极小 |
|
上最大值为13……………………………………………………（12分）
（3）上单调递增
又
依题意
上恒成立.
①在
|
③在
综合上述讨论可知，所求参数b取值范围是：b≥0………………………………（12分）
22．（本小题满分14分）
（文）解：（1）直线l过点（3，－）且方向向量为
……………………………………（4分）
（2）设直线
，
由
……………………………………………………（7分）
将
，
整理得
|
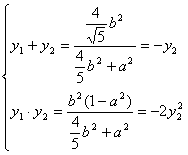（9分）
由①2/②知 
……………………………………（12分）
又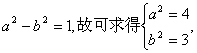
因此所求椭圆方程为：
…（14分）
|
）且方向向量为
化简为：
…………（4分）
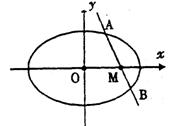
（2）设直线
交于两点A（x1,y1），B（x2,y2），和x轴交于M（1，0）
由
………………………………………………（7分）
将
…………………………………………①
|
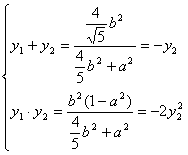
由②2/③ 知：32b2=（4b2+5a2）（a2－1）…………………………………………（10分）
化为
………………………………………………④
对方程①求判别式，且由△>0
即
化简为：
………………………………………………⑤
由④式代入⑤可知：
又椭圆的焦点在x轴上，
则
由④知：
因此所求椭圆长轴长2a范围为（