高三9月份月考数学试卷
数学试卷(理科)
注意：请将选择题和填空题的答案填在答题卷上，交卷时只交答题卷
一．选择题 (本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项符合题目的要求，请将每小题正确答案前的字母填入答题卡的表格中)
1．（1－ｉ）4＝（ ）
A．4 B. –4 C. 4ｉ D. – 4ｉ
2．用数学归纳法证
的过程中，当n=k到n=k+1时，左边所增加的项为：
（ ）
3．已知盒中装有3只螺口与7只卡口灯炮，这些灯炮的外形与功率都相同且灯口向
下放着，现需要一只卡口灯炮使用，电工师傅每次从中任取一只并不放回，则他直
到第3次才取得卡口灯炮的概率为 （ ）
A．
B．
C．
D．
4． 函数y=
的导数是 （
）
A．—
B．
C．— D．—
5．在抽查产品尺寸的过程中，将其尺寸分成若干组，[a,b]是其中的一组。已知该组
的频率为m，该组上的直方图的高为h，则a-b等于 （ ）
A．mh B．
C．
D．m+h
6．设随机变量x服从正态分布N(0,1)，记j(x)=P(x<x)，则下列结论不正确的是（ ）
A．j(0)=0.5 B．j(x)=1－j(－x) C．P(x<a)=2 j(a)－1 D．P(x＞a)=1－ j(a)
7. 设y=8x2-lnx，则此函数在区间(0,1/4)和(1/2,1)内分别为（ ）
A．单调递增，单调递减 B、单调递增，单调递增
C、单调递减，单调递增 D、单调递减，单调递减
8．曲线y=x3+x-2 在点P0处的切线平行于直线y=4x-1，则点P0点的坐标是（ ）
A．(0,1) B.(1,0) C.(-1,0) D.(1,4)
9. 函数y=2x3-3x2-12x+5在[0,3]上的最大值与最小值分别是（ ）
A．5 , -15 B．5 , 4 C．4 , -15 D．5 , -16
10. 同时抛掷4枚均匀的硬币80次，设4枚硬币正好出现2枚正面向上，
2枚反面向上的次数为ξ，则ξ的数学期望是（ ）
A．20 B．25 C．30 D．40
11．已知A（0，0）、B（a，b），P1是AB的中点，P2是BP1的中点， P 3是P1P2的中点，……，P n+2是PnPn+1的中点，则Pn点的极限位置是（ ）
A．（
，
） B．（
，
） C．（
，
）
D．（
，
）
12．给出下列命题：
（1） 若函数f(x)=x，则f′(0)=0；
（2） y=2cosx+lgx，则y′= -2cosx·sinx+
;
（3） 函数在某一点的导数不存在，则这一点的切线也不存在；
（4） 若函数在某一点连续，则在这一点必有极限；
其中正确的命题有（ ）
A． 0个 B.1个 C．2个 D．3个
二．填空题 (每小题4分，共16分，把答案填在答题卡中的横线上)
13. 一工厂生产了某种产品16800件，它们来自甲．乙．丙3条生产线，为检查这批产品的质量，决定采用分层抽样的方法进行抽样，已知甲．乙．丙三条生产线抽取的个体数组成一个等差数列，则乙生产线生产了 件产品；
14. 已知复数ｚ0＝３＋２ｉ，复数ｚ满足ｚ·ｚ0＝3z＋ｚ0，则复数
z＝ ；
15．若
，则m ＝________ , n
＝________；
16．过曲线
上的点（3，
）的切线方程（一般式）为_________．
无为严桥中学2005~2006年度高三9月份月考
数学答题卷(理科) 命题人:任士武
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得分 |
|
|
|
|
|
|
|
|
|
一．选择题 (本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项符合题目的要求，请将每小题正确答案前的字母填入下列表格中)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
二．填空题 (每小题4分，共16分，把答案填在下面的横线上)
13、 14、 15、m ＝___ , n ＝___ 16、
三．解答题：（本大题共6小题，17~21每小题12分，22题14分，共74分）
17．已知 a1=
，且Sn = n2an 
（1） 求a2 ，a3 ，a4
（2） 猜测{ an}的通项公式，并用数学归纳法证明之.
18．设函数
，其中
；
（1）若
在
处取得极值，求常数
的值；
（2）若在
上为增函数，求的取值范围．
19．从4名男生和2名女生中任选3人参加演讲比赛，设随机变量x表示所选3人中男生的人数．
⑴求x的分布列及数学期望；
⑵求“所选3人中女生不超过１人”的概率．
20．已知函数
.
（1）当
时，求函数的最小值；
（2）若对任意
恒成立，试求的取值范围.
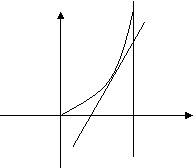
21．如图，由y=0，x=8，y=x2围成的曲边三角形，在曲线弧OB上求一点M，使得过M所作的y=x2的切线PQ与OA，AB围成的三角形PQA面积最大。
22．某城市有甲、乙、丙3个旅游景点，一位客人游览这三个景点的概率
分别是0.4，0.5，0.6，且客人是否游览哪个景点互不影响，设ξ表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值．
（Ⅰ）求ξ的分布列及数学期望；
（Ⅱ）记“函数f(x)＝x2－3ξx＋1在区间[2，＋∞
上单调递增”为事件A，求事件A的概率.