高三代数综合检测试题（二）
班级 姓名 总分
一.选择题：（本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的）
1．
=（ ）
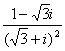A.
B.-
C.
D.
2.集合A={yy=log2x,x＞0},B={yy=(
)x,x＞0},则A
B等于（ ）
A．（0，） B．（0，1） C．（，1） D．（1，2）
3.已知x
,cosx=
,则tan2x=( ) A. 
B. - C. 
D. -
4.设函数f(x)={
.若f(x0)＞1,则x0的取值范围是（ ）
A.(-1,1) B.(-1,+∞) C.(-∞,-2)
D.
5.O是平面上一定点,A、B
、C是平面上不共线的三个点，动点P满足
,则P的轨迹一定通过三角形ABC的（ ）
A.外心 B.内心 C.重心 D.垂心
6.曲线y=lnx-x2+
在点M（1，0）处的切线方程为（ ）
A.3x+2y-3=0 B.2x+3y+3=0 C.x+2y-1=0 D.2x+y-1=0
7.函数y=ln
的反函数为(
)
A.y=
B.y=
C.y=
D.y=
8.已知定义域为R的偶函数f(x)在[0,+
上是增函数，且f()=0,则不等式f(log4x)＞0的解集为（ ）A.{xx＞2}
B.{x0﹤x﹤} C.{x0﹤x﹤或x＞2} D.{x﹤x﹤1或x＞2}
9.已知方程(x2-2x+m)(x2-2x+n)=0的四个根组成一个首项为
的等差数列，则m-n=( ) A.1 B.
C. D. 
10.
=(
) A. 3 B. 
C. 
D. 6
11.某种细胞开始时有2个，1小时后分裂成4个并死去1个，2小时后分裂成6个并死去1个，3小时后分裂成10个并死去1个……按照此规律，6小时后细胞存
活数是（ ） A. 33 B. 64 C. 66 D. 127
12.f(x)是定义在区间[-c,c]上在奇函数，其图象如图所示.令g(x)=af(x)+b,则
下列关于函数g(x)的叙述正确的是 （ ）
A.若a﹤0，则函数g(x)的图象关于原点对称 B.若a=1,0﹤b﹤2,则方程g(x)=0有大于2的实根C.若a= -2,b=0,则函数g(x)的图象关于y轴对称 D.若a
,b=2,则方程g(x)=0有三个实根.
二．填空题：（本大题共4小题，每小题4分，共16分。把答案填在题中横线上）
13.①(x2-
)9展开式中x9的系数是
②
（
）=
14.①函数y=x3-ax+2在x= -2处有极值，则a= ②在杨辉三角中，斜线AB上方一斜行的前n个数字和S(n)=1+3+6+…,则
=______
15.某公司生产三种型号的轿车，产量分别为1200辆，6000辆和2000辆。为检验该公司的产品质量，现用分层抽样的方法抽取46辆进行检验，这三种型号的轿车依次应抽取 、
、 辆。
16.某城市在中心广场建造一个花圃，花圃分为6个部分。现要栽种4种
不同颜色的花，每部分栽种一种且相邻部分不能栽种同样颜色的花，不同 47页图
的栽种方法有 种（用数字作答）
三．解答题：（本大题共6小题，共74分。解答应写出文字说明，证明过程或演算步骤）
17．已知函数f(x)=2sinx(sinx+cosx).（1）求函数f(x)的最小正周期和最大值；（2）画出函数y=f(x)在区间[
]上的图象.
18.已知函数f(x)=
-log2
，求函数f(x)的定义域，并讨论它的奇偶性和单调性.
19.A、B两个代表队进行乒乓球对抗赛，每队三名队员，A队队员是A1，A2，A3，B队队员是B1，B2，B3，按以往多次比赛的统计，对阵队员之间胜负概率如下：
| 对阵队员 | A队队员胜的概率 | A队队员负的概率 |
| A1对B1 | |
|
| A2对B2 | |
|
| A3对B3 |
|
|
现按表中对阵方式出场，每场胜队得1分，负队得0分。设A队、B队最后所得总分分别为ξ、η.（1）求ξ、η的概率分布；（2）求Eξ，Eη.
20.某公司取消福利分房和公司医疗，实行年薪制工资结构改革，该公司从2000年初起，每人的工资由三个项目组成并按下表规定实施；如果该公司今年有5位职工，计算从明年起每年新招5名职工。
| 项目 | 金额（元/人 | 性质与计算方法 |
| 基础工资 | 10000 | 考虑物价因素，从2000年初起每年递增10%（与工资无关） |
| 房屋补贴 | 400 | 按职工到公司年限计算，每年递增400元 |
| 医疗费 | 1600 | 固定不变 |
年）（1）若2000年算第一年，试把第n年该公司付给职工工资总额y（万元）表示为年限n的函数；（2）试判断公司每年发给职工工资总额中，房屋补贴和医疗费的总和能否超过基础工资总额的20%？
21.已知常数a＞0,向量
.经过原点O以
为方向向量的直线与经过定点A(0,a)以
为方向向量的直线相交于点P，其中
.试问：是否存在两个定点E、F，使得PE+PF为定值.若存在，求出E、F的坐标；若不存在，说明理由.
22.设a0为常数，且an=3n-1-2an-1(n
N).(1)证明对任意n
]+(-1)n
;(2)假设对任意n≥1有an＞an-1，求a0的取值范围。
答案：选择题：BBDDB CBCCB CB 填空题：13. -
,-1; 14.12,6; 15. 6,30,10; 16.120
三．解答题：17.（1）最小正周期为
，最大值为1+
；（2）图略
18．由题意易知，f(x)的定义域为（-1，0）
（0，1）；f(x)是奇函数；在（-1，0）和（0，1）内是单调递减函数。
19．（1）略（2）Eξ=
，Eη=
20．（1）y=5n(1+
)n+0.1
n(n+1)+0.8n（万元）;(2)不能.
21.由题意易知，直线OP和AP的方程分别为
y=ax和y-a=-2ax.消去参数，即有y(y-a)=-2a2x2,整理得，
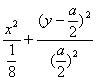=1 ①
a＞0,
有：（i）a=
时，方程①是圆方程，故不存在符合题意的定点E和F；（ii）当0﹤a﹤时, 方程①表示椭圆，焦点E（
）和F（
）为符合题意的两个定点：（iii）当a＞时，方程①也表示椭圆，焦点E（0，
）和F（0，
）为符合题意的两个定点。
22．（1）用数学归纳法；（2）由通项公式有an-an-1=
, an＞an-1(n
)等价于（-1）n-1(5a0-1)﹤
(n). ①
(i)当n=2k-1,k=1,2,…时，①即为（-1）2k-2(5a0-1)﹤
，即a0﹤
+.②
②对k=1,2,…都成立，有a0﹤
+=.
(ii)当n=2k, k=1,2,…时，①即为（-1）2k-1(5a0-1)﹤
,即为a0＞-+.③
③对k=1,2,…都成立，有a0＞-
+=0.综上，①对任意(n)成立，有0﹤a0﹤.故a0的取值范围为（0，）