高三代数综合检测试题(三)
班级 姓名 总分
一、选择题:(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只
有一项是符合题目要求的)
1.设集合A={xx![]() 且x2-3x+2=0},B={xcos
且x2-3x+2=0},B={xcos![]() x=0, x
x=0, x![]() },全集U={-3,-2,-1,0,1,2,3},则CUA
},全集U={-3,-2,-1,0,1,2,3},则CUA![]() B=( )
A.{-3,-1,0,3}
B.{-3,-1,1,3}
C.{-3,-1,3}
D.{-3,3}
B=( )
A.{-3,-1,0,3}
B.{-3,-1,1,3}
C.{-3,-1,3}
D.{-3,3}
2.等比数列{an}的首项a1=3,前n项和为Sn,若![]() ,则
,则![]() Sn等于( )
Sn等于( )
A. 2 B. 6 C. -2 D.-6
3.某地区高中分三类,A类校共有学生4000人,B类校共有学生2000人,C类校共有学生3000人,现欲抽样分析某次考试的情况,若抽取900份试卷进行分析,则从A类校抽取的试卷份数应为 ( ) A. 450 B.400 C. 300 D.200
4.y=sin(2x+![]() )cos(x-
)cos(x-![]() )-cos(2x+
)-cos(2x+![]() )sin(x-
)sin(x-![]() )的图象中一条对称轴是( )
)的图象中一条对称轴是( )
A.x=![]() B.x=
B.x=![]() C.x=
C.x=![]() D.x=
D.x=![]()
5.在生产过程中用的质量控制图,其制作的主要依据是( )
A.工艺要求 B.小概率事件在一次实验几乎不可能发生原理 C.生产条件 D.企业标准
6.如果复数z满足z+i+z-i=2,那么z+i+1的最小值的( )
A.1
B.![]() C.2 D.
C.2 D.![]()
7.![]() (2n-
(2n-![]() )=1,则k的值等于( )
)=1,则k的值等于( )
A. 1 B. 2 C. 3 D.4
8.已知直线x=1是函数y=f(2x)图象的一条对称轴,那么函数y=f(3-2x)的图象关于( )
A.直线x=![]() 对称 B.直线x=-
对称 B.直线x=-![]() 对称 C.直线x=
对称 C.直线x=![]() 对称 D.直线x=-
对称 D.直线x=-![]() 对称
对称
9.某种产品有4只次品和6只正品,每只产品均不相同且可区分,今每次取出一只测试,直到4只次品全测出为止,则最后一只次品恰好在第五次测试时被发现的不同情况种数是( ) A. 24 B.144 C. 576 D.720
10.中国政府正式加入世贸组织后,从2002年开始汽车进口关税将大幅下调,若一辆进口汽车2001年售价为30万元,五年后(2006年)售价为y万元,每年下调率平均为x%,那么y与x的函数关系式为( )
A.y=30(1-x%)6 B.y=30(1+x%)6 C.y=30(1-x%)5 D.y=30(1+x%)5
11.已知x1是方程x+2x=4的根,x2是方程x+log2x=4的根,则x1+x2的值所在区间是( )
A.(0,1) B.(1,3) C.(3,5) D.(5,+![]() )
)
12.若函数y=![]() 的图象如图所示,则a的范围是( )
的图象如图所示,则a的范围是( )
A. (-![]() )
B.(0,3) C.
(1,3) D.(2,3)
)
B.(0,3) C.
(1,3) D.(2,3)
二.填空题:(本大题共4小题,每小题4分,共16分,把答案填在题中横线上)
13.①设x0是f(x)=![]() (ex+e--x)的最小值点,则曲线在点(x0,f(x0))处的切线方程是
(ex+e--x)的最小值点,则曲线在点(x0,f(x0))处的切线方程是
②若(3x-1)n(n![]() N)展开式中各项系数的和为128,则展开式中x2项的系数为
N)展开式中各项系数的和为128,则展开式中x2项的系数为
14.①一个箱子内有9张票,其号数分别为1,2,3,…,9,从中任意取两张,其号数至少有一个是奇数的概率为 .②设![]() 、
、![]() 是两个互相垂直的单位向量,且
是两个互相垂直的单位向量,且![]() ,
,![]()
![]() ,若
,若![]() ,则
,则![]() 的值为
的值为
15.①等比数列{an}的前n项和为Sn,若S3=2,S6=6,则a10+a11+a12=_____
②在等差数列{an}中,已知3(a3+a5)+2(a7+a10+a13)=24,则此数列的前13项的和为_____
16.给出下列4个命题:①函数y=-sin(k![]() )(k
)(k![]() )是奇函数;②函数y=tanx的图象关于点(k
)是奇函数;②函数y=tanx的图象关于点(k![]() )(k
)(k![]() )对称;③函数y=(sinx+cosx)2+cos2x的最大值为3;④函数y=sin(2x+
)对称;③函数y=(sinx+cosx)2+cos2x的最大值为3;④函数y=sin(2x+![]() )的图象由y=sin2x的图象向左平移
)的图象由y=sin2x的图象向左平移![]() 个单位得到.其中正确命题的序号是____ (把你认为正确命题序号都填上).
个单位得到.其中正确命题的序号是____ (把你认为正确命题序号都填上).
三.解答题:(本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤)
17.已知函数f(x)=![]() ,将函数y=f-1(x)的图象向左平移2个单位,再向上平移1个单位,就得到y=g(x)的图象.(1)写出y=g(x)的解析式;(2)求出F(x)=g(x2)-f-1(x)的最小值及取得最小值时x的值.
,将函数y=f-1(x)的图象向左平移2个单位,再向上平移1个单位,就得到y=g(x)的图象.(1)写出y=g(x)的解析式;(2)求出F(x)=g(x2)-f-1(x)的最小值及取得最小值时x的值.
18.三角形ABC中,BC=a,AC=b,a,b是方程x2-2![]() x+2=0的两根,且2cos(A+B)=1.求:(1)角C的度数;(2)AB的长;(3)S
x+2=0的两根,且2cos(A+B)=1.求:(1)角C的度数;(2)AB的长;(3)S![]() .
.
19.已知f(A![]() B)=sin22A+cos22B-
B)=sin22A+cos22B-![]() sin2A-cos2B+2.(1)设A、B、C为
sin2A-cos2B+2.(1)设A、B、C为![]() ABC内角,当f(A
ABC内角,当f(A![]() B)取得最小值时,求
B)取得最小值时,求![]() ;(2)当A+B=
;(2)当A+B=![]() 且A、B
且A、B![]() 时,y=(A
时,y=(A![]() B)的图象通过向量
B)的图象通过向量![]() 的平移得到函数y=2cos2A的图象,求向量
的平移得到函数y=2cos2A的图象,求向量![]() .
.
20.某自来水厂的蓄水池中存有400吨水,水厂每小时可向蓄水池中注入60吨水,同时蓄水池又向居民小区不间断地供水,t小时内供水总量为120![]() 吨(0
吨(0![]() )。(1)从供水开始到第几小时,蓄水池中的水量最少?最少水量有多少吨?(2)若蓄水池中的水量少于80吨就会出现供水紧张现象,试问:在一天24小时内,有几小时会出现供水紧张现象?
)。(1)从供水开始到第几小时,蓄水池中的水量最少?最少水量有多少吨?(2)若蓄水池中的水量少于80吨就会出现供水紧张现象,试问:在一天24小时内,有几小时会出现供水紧张现象?
21.已知二次函数y=f(x)经过点(0,10),导函数f/(x)=2x-5,当x![]() 时,f(x)是整数的个数记为an.(1)求数列{an}的通项公式;(2)令bn=
时,f(x)是整数的个数记为an.(1)求数列{an}的通项公式;(2)令bn=![]() ,求数列{an+bn}的前n(n
,求数列{an+bn}的前n(n![]() )项和Sn.
)项和Sn.
22.设函数f(x)是定义在[-1,0)![]() (0,1]上的奇函数,当x
(0,1]上的奇函数,当x![]() 时,f(x)=2ax+
时,f(x)=2ax+![]() (a为实数).(1)当x
(a为实数).(1)当x![]() 时,求f(x)的解析式;(2)若a>-1,试判断f(x)在(0,1]上的单调性,并证明你的结论;(3)是否存在a,使得当 x
时,求f(x)的解析式;(2)若a>-1,试判断f(x)在(0,1]上的单调性,并证明你的结论;(3)是否存在a,使得当 x![]() 时,f(x)有最大值-6.
时,f(x)有最大值-6.
答案:一.选择题:CABCB ADACC CC
一.
填空题:13.①y=1, ②-189;14.①![]() ,②2;15.①16,②26;16. ①②
,②2;15.①16,②26;16. ①②
二.
解答题:17.(1)g(x)=log2(x+2)(x>-2);(2)x=![]() 时,Fmin=
时,Fmin=![]() .
.
18.(1)1200,(2)![]() ,(3)
,(3)![]() ;
;
19.(1)f(A![]() B)=(sin2A-
B)=(sin2A-![]() )2+(cos2B-
)2+(cos2B-![]() )2+1.由题意{
)2+1.由题意{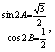
![]()
![]() 或
或![]()
(2)![]() A+B=
A+B=![]()
![]() ,
,![]() f(A
f(A![]() B)= cos2A-
B)= cos2A-![]() sin2A+3=2cos(2A+
sin2A+3=2cos(2A+![]() )+3,
)+3,
易知,![]() =(
=(![]() ,-3)
,-3)
20.(1)从供水开始到第6小时,蓄水池中的水量最少,为40吨;(2)8小时。
21.(1)an={![]() (2)n2-3n+
(2)n2-3n+![]()
22.(1)f(x)=2ax-![]() ;(2)增函数;证明略;(3)存在a=-2
;(2)增函数;证明略;(3)存在a=-2![]() ,使f(x)在(0,1]上有最大值-6.
,使f(x)在(0,1]上有最大值-6.