高三第二次阶段性检测试卷数学试卷

高三第二次阶段性检测试卷数学试卷(理科)

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．做120分钟，共150分

第Ⅰ卷

一. 选择题:( 本大题共12小题, 每小题5分，共60分)

1.已知集合，若，则等于（　　）

A、1　　　　　　　  B、2　　　　　　　　 C、1或2　　　　　　  D、1或2.5

2.若，则　　　　　　　　　　　　　　　　　　　 （　　　）

A、　　　　　　　 B、　　　　　　 C、　　　　　　 D、

3.已知，若，则的值等于　　　　　　　　  （　　　）

A、　　　　　　　  B、　　　　　　　  C、　　 　　　　 D、

4.已知，其中则满足条件的不共线的向量共（　　 ）

A、16个　　　　　　　B、13个 　　　　　  C、12个　　 　　　　D、9个

5.已知F₁、F₂为双曲线的焦点，过F₂作垂直于x轴的直线，它与双曲线的一个交点为P，且，则双曲线的渐近线方程为 　　　　　  （　　　 ）

A、　　　　B、　 　　C、　　　D、

6.若向量，则与一定满足　　　　　　  （　　　 ）

A、与的夹角等于　　 B、　　 C、　 D、

7. 是定义在上的奇函数，它的最小正周期为，则的值为　　　（　　　 ）

A、0　　　　　　  B、　　　　　　　 C、　　　　　　　 D、

8. 设为两两不重合的平面,l,m,n为两两不重合的直线,给出下列四个命题:

①　　　 若②若

③④

其中真命题的个数是　　　　　　　　　　　　　　　　　　　　　　　　 ( 　 )

　 A 、 1　　　　　　  B　2　　　　　　  ( C ) 3　　　　　 ( D )4

9.点是直线上的动点，则代数式有　（　　 ）

A、最大值8　　　　　 B、最小值8　　　　  C、最小值6　　　　D、最大值6

10.在等差数列{}中,若,则的值为（　　　）

A、20　　　　　　 B、22　　　　　　 C、24　　　　　　 D、28

11.设，下列命题：①即不是奇函数，又不是偶函数；②若是三角形内角，则是增函数；③若是三角形内角，则有最大值无最小值；④的最小正周期为。其中正确命题的序号是（　　 ）

A、①②　　　　　　  B、①③　　　　　　　 C、②③　　　　　　  D、②④

12.某商场开展促销抽奖活动, 摇奖器摇出的一组中奖号码是8, 2, 5, 3, 7, 1, 参加抽奖的每位顾客从0, 1, 2, 3, 4, 5, 6, 7, 8, 9这十个号码中任意抽出六个组成一组, 如果顾客抽出的六个号码中至少有五个与摇奖器摇出的号码相同(不计顺序)就可以得奖. 设一位顾客可能抽出的不同号码组共有m组, 其中可以中奖的号码共有n组, 则的值为　　　　　　  (　　  )

A. 　　　　　　　　B. 　　　　　　 C. 　　　　D.

第Ⅱ卷

二. 填空题：(本大题共6小题，每小题4分，共24分)

13. 展开式中, 的系数是　　　　　　 . (用数字作答)

14.设抛物线的一条弦以为中点，则该弦所在直线的斜率为　　 　　.

15. 若实数x, y满足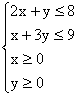, 则的最大值为　　　　　　  .

16. 已知斜率为的直线被圆所截，截得的弦的长等于　　　　　　　 .

17. 已知奇函数满足条件, 且当 时,,则的值是　　　　　　　 .

18. 有以下四个命题

①的最小值是②已知, 则

③在R上是增函数

④函数的图象的一个对称点是

其中真命题的序号是　　　 　　　　　　　 (把你认为正确命题的序号都填上)

三. 解答题：(本大题5小题，共66分)

19. (本题12分)已知是两个不共线的向量，且.

（Ⅰ）求证：与垂直；

（Ⅱ）若，且，求的值。

20. (本题12分)已知函数在处有极值，曲线在处的切线平行于直线试求函数的极大值与极小值的差。

21. (本题14分) 如图, 四棱锥P－ABCD的底面是正方形, PA⊥底面ABCD, PA＝AD＝2, 点M、N

分别为棱PD、PC的中点.

(1) 求证: PD⊥平面AMN；

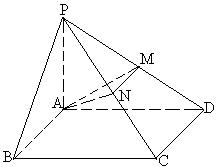(2) 求直线PB与平面AMN所成角的大小；　　　　　　　　 

(3) 求二面角P－AN－M的大小。

　　　　  　　　　　　　　　　　　　　　

22.（本题14分）已知等差数列{a_n}，公差大于0，且的两根，数列{b_n}前n项和为，且

（Ⅰ）写出数列{a_n}、{b_n}的通项公式；

（Ⅱ）记.

23.（本题14分）已知为抛物线上任意一点, 直线l为过点A的切线, 设直线l交y轴于点B. Pl, 且.

(1) 当A点运动时, 求点P的轨迹方程;

(2) 求点到动直线l的最短距离, 并求此时l的方程.