高三第二次数学调研考试
注意事项：
1．答卷前，考生先将自己的姓名、考试证号等填写清楚，并认真核准答题卡表头及答题纸密封线内规定填写或填涂的项目．
2．第Ⅰ卷选择题部分的答案必须使用2B铅笔填涂在答题卡上；第Ⅱ卷非选择题部分的答案必须使用黑色签字笔书写在答题纸上，字体工整、笔迹清楚．
3．请按照题号顺序在各题目的答题区域内作答，书写不能超出横线或方格，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效．
保持卡面和答题纸清洁，不折叠、不破损．
数 学
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．全卷满分150分，考试时间120分钟．
参考公式：
如果事件A、B互斥，那么P（A+B）=P（A）+P（B）
如果事件A、B相互独立，那么P（A·B）=P（A）·P（B）
如果事件A在一次试验中发生的概率是P，那么n次独立重复试验中恰好发生k次的概率
正棱锥、圆锥的侧面积公式S锥体侧=
其中c表示底面周长，
表示斜高或母线长
球的体积公式
球= 
其中R表示球的半径
第Ⅰ卷（选择题 共50分）
一、选择题：本大题共10小题每小题5分；共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1． 命题“若a＞b，则a－8＞b－8”的逆否命题是
A．若a＜b，则a－8＜b－8 B．若a－8＞b－8，则a＞b
C．若a≤b，则a－8≤b－8 D．若a－8≤b－8，则a≤b
2．
椭圆
的右焦点到直线y=
x的距离是
A．
B．
C．1
D．
3．
在等比数列{an}中，a5a7=6，a2+a10=5，则
等于
A．－
或－
B．
C．
D．或
4． 将函数y=sin2x的图象按向量a平移后得到函数y=sin(2x－
)的图象，则向量a可以是
A．(，0) B．(
，0)
C．(－，0) D．(－，0)
5． 如图，长方体ABCD—A1B1C1D1中，∠DAD1=45
，∠CDC1=30，
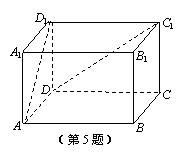那么异面直线AD1与DC1所成角的大小为
A．
B．
C．
D．
6． 
的值等于
A．1022 B．1023 C．2046 D．2047
7．
已知sinα＞0，cosα＞0，且sinαcosα＞
，则α的取值范围是
A．(2kπ+
，2kπ+
)， k∈Z
B．(kπ+，kπ+
)， k∈Z
C．(2kπ+
，2kπ+
)， k∈Z D．(kπ+，kπ+
)， k∈Z
8． 定义在R上的函数f（x）对任意的实数x，满足f（x +1）=－ f（x－1），则下列结论一定成立的是
A．f（x）是以4为周期的周期函数
B．f（x）是以6为周期的周期函数
C．f（x）的图象关于直线x=1对称
D．f（x）的图象关于点（1，0）对称
9． 甲、乙两人玩猜骰子游戏．游戏的规则是：有三个骰子（每个骰子都是正方体，其六个面上分别标有数字1，2，3，4，5，6），乙先从1，2，3，4，5，6这六个数中报一个，然后由甲掷这三个骰子各一次，如果三个骰子中至少有1个骰子的向上一面的数字恰好是乙所报的这个数，那么乙获胜，否则甲获胜．若骰子任意一面向上的概率均等，则乙获胜的概率是
A．
B．
C．
D．
10．已知平面上点P∈{(x，y)
（α∈R）}，则满足条件的点P在平面上所组成图形的面积是
A．36π B．32π C．16π D．4π
第Ⅱ卷（非选择题，共100分）
二、填空题：本大题共4小题；每小题4分，共16分．
11．函数f（x）=6cosx+cos2x的最小值是 ．
12．已知椭圆
与双曲线
（m>0，n>0)具有相同的焦点F1，F2，设两曲线的一个交点为Q，∠QF1F2=90°，则双曲线的离心率为
．
13．函数f(x)=lg（x2－ax－1）在区间(1，+∞)上是单调增函数，则a的取值范围是 ．
14．设函数f(x)定义域为R．若存在与x无关的正常数M，使f(x) ≤Mx对一切实数x均成立，则称f(x)为有界泛函．在函数f(x)=2x，g(x)=x2，h(x)=2x，v(x)=xsinx中，属于有界泛函的有 ．
三、解答题：本大题共6小题；共84分．解答应写出文字说明、证明过程或演算步骤．
15．（本小题满分14分）
已知Sn是等比数列{an}的前n项和，S3，S9，S6成等差数列．
（1）求数列{an}的公比q；
（2）问a4，a7的等差中项是数列{an}中的第几项？请说明理由．
16．（本小题满分14分）
已知向量a=（1，2），b=（－2，1），k，t为正实数，向量x= a +(t2+1)b，y=－k a+
b．
（1）若x⊥y，求k的最小值；
（2）是否存在正实数k，t，使x∥y？若存在，求出k的取值范围；若不存在，请说明理由．
17．（本小题满分15分）
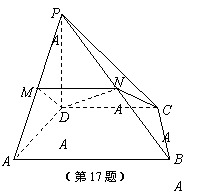在四棱锥P—ABCD中，AD⊥AB，CD∥AB，PD⊥底面ABCD，
=
，直线PA与底面ABCD成60°角，点M、N分别是PA、PB的中点．
（１）求二面角P—MN—D的大小；
（２）如果△CDN为直角三角形，求
的值．
18．（本小题满分13分）
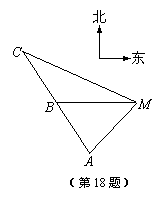
如图，已知A、B、C是一条直路上的三点，AB与BC各等于1km，从三点分别遥望塔M，在A处看见塔在北偏东45°方向，在B处看见塔在正东方向，在点C处见塔在南偏东60°方向，求塔到直路ABC的最短距离．
19．（本小题满分15分）
设定义在R上的函数
（其中
∈R，i =0，1，2，3，4），当x=－1时，f(x)取得极大值，并且函数y=f(x+1)的图象关于点（－1，0）对称．
（1）求f(x)；
（2）试在函数f(x)的图象上求两点，使这两点为切点的切线互相垂直，且切点的横坐标都在区间
上；
（3）若
(n∈N+)，求证：
．
20．（本小题满分13分）
设M是椭圆C：
上的一点，P、Q、T分别为点M关于y轴、原点、x轴的对称点， N为椭圆C上异于点M的另一点，且MN⊥MQ，QN与PT的交点为E，当M沿椭圆C运动时，求动点E的轨迹方程．