高三第二次月考数学试卷(理科)
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一个选项是符合题目要求的。
1.设M={-1,0,1},N={-2,-1,0,1,2},对于M的所有元素x,使x+f(x)均为偶数,则从M到N的映射f的个数是( )
A.7 B.12 C.0 D.以上都不对
2.设全集I={(x,y)x,y∈R},集合P={(x,y)y=x2+2bx+1},Q={(x,y)y=2a(x+b)},S={(a,b)P∩Q=![]() },则S的面积是( )
},则S的面积是( )
A.1 B.![]() C.4 D.2
C.4 D.2![]()
3.定义在R上的函数f(x)不是常数函数,且满足f(x-1)=f(x+1),f(x+1)=f(1-x)则f(x)( )
A.是奇数也是周期函数 B.是偶函数也是周期函数
C.是奇函数但不是周期函数 D.是偶函数但不是周期函数
4.已知f(x)=ax (a>0且a≠1) f-1(2)<0,则f-1(x+1)的图象是( )
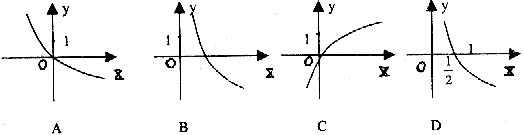
5.在数列{an}中,a1, a2, a3, 成等差数列,a2, a3, a4 成等比数列,a3, a4, a5 的倒数成等差数列,则a1, a3, a5是( )
A.等差数列 B.等比数列
C.三个数的倒数成等差数列 D.三个数的平方成等比数列
6.等差数列{an}中,Sn是前n项和,且S3=S8,S7=SK,则K为( )
A.4 B.11 C.2 D.12
7.函数y=f(x) x∈[a,b] A={(x, y) y=f(x) x∈[a,b]},B={(x, y ) x=1},则A∩B中所含元素的个数( )
A.0 B.1 C.0或1 D.0、1或2
8.a1=3, a2=6且an+2=an+1-an,则a2003=( )
A.-3 B.3 C.-6 D.6
9.在等差数列{an}中,满足3a4=7a7且a1>0, Sn是数列{an}的前n项和,若Sn取得最大值,则n等于( )
A.7 B.8 C.9 D.10
10.已知奇数f(x)和偶函数g(x)满足:f(x)+g(x)=ax-a-x+2且g(b)=a, 则f(a)的值为( )
A.a2 B.2 C.17/4 D.15/4
11.定义在R上的函f(x)是增函数A(0,-1) B(3,1)是其图象上的两点那么不等式f(x+1)<1的解集为( )
A.![]() B.(-1,2) C.
B.(-1,2) C.![]() D.
D.![]() (2,+∞)
(2,+∞)
12.某学生离家去学校,为了锻炼身体,一开始跑步前进,跑累了再走余下的路程,下图中纵轴表示离校的距离,横轴表示出发的时间,则下列四个图形中符合该学生走法的可能是( )
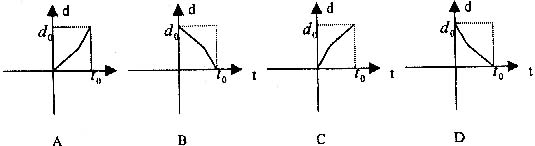
二、填空题:本大题共4小题,每小题4分,共16分。把答案填在题中横线上。
13.集合M={(x, y)xy=1 x>0} ,在映射f:M→N作用下,点(x, y)的象为(log2x, log2y),而N恰为象的集合,则N={(x, y) }
14.在等差数列{an}中,若a10=0,则有等式a1+a2+…+an=a1+a2+…+a19-n(n<19 n∈N+)成立,类比上述性质,相应地在等比数列{bn}中,若b9=1,则有等式
15.设函数f(n)=k(其中n∈N+),k是![]() 的小数点后的第n位数字,
的小数点后的第n位数字,![]() =3.…则
=3.…则![]() =
=
16.给出下列函数
(1)函数y=ax (0<a且a≠1)与函数y=logaax (a>0且a≠1)的定义域相同
(2)函数y=x3与函数y=3x的值域相同。
(3)函数![]() 与函数
与函数![]() 均是奇函数.
均是奇函数.
(4)使函数![]() 在区间(-2,+∞)上为增函数的a的范围是
在区间(-2,+∞)上为增函数的a的范围是![]() 则正确命题的序号为
则正确命题的序号为
三、解答题:本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤。
17.已知关于x的方程x=ax+1有一个负根而且没有正根
求a的取值范围(本小题十二分)
18.设A={x 1<x<3},又设B是关于x的不等式组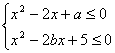 的解集,试确定a,b的取值范围使A
的解集,试确定a,b的取值范围使A![]() B(本小题十二分)
B(本小题十二分)
19.数列{an}中,相邻两项an, an+1是方程x2+3nx+bn=0的两根,已知a10=-17
求:b51的值(本小题十二分)
20.设f(x)是定义在[-1,1]上的偶函数,f(x)与g(x)的图象关于x-1=0对称,且当x∈[2,3]时,g(x)=a(x-2)-2(x-2)3 (a为常数)
(1)求f(x)的解析式
(2)若f(x)在[0,1]上是增函数,求实数a的取值范围
(3)若a∈(-6,6),问能否使f(x)的最大值为4(本小题十二分)
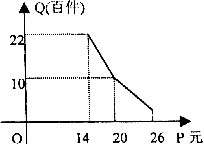
21.在对口脱贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型残疾人企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活开支3600元后,逐步偿还转让费(不计息),在甲提供的资料中有:①这种消费品的进价每件14元;②该店月销售量Q(百件)与销售价格P(元)的关系如图;③每月需要各种开支2000元
(1)试问为使该店至少能够维持职工生活,商品价格应控制在何范围内?
(2)当商品的价格为每件多少元时,月利润扣除职工最低生活费后的余额最大并求最大余额
(3)企业乙只依靠该店,最早可望在几年后脱贫?(本小题十二分)
22.已知f(x)是定义在R上的不恒为零的函数,且对于任意的a,b∈R都满足:f(a·b)=af(b)+bf(a)
I.求f(0)、f(1)的值
II.判断f(x)的奇偶性,并证明你的结论;
III.F(2)=2,![]() (n∈N*),求数列{un}的前n项的和Sn(本小题十四分)
(n∈N*),求数列{un}的前n项的和Sn(本小题十四分)
高三参考答案数学(理科)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | B | B | A | B | A | C | C | C | D | B | D |
二、填空题
13.x+y=0 14.b1b2…bn=b1b2…b17-n (n<17) 15.1 16.①、③
 三、解答题
三、解答题
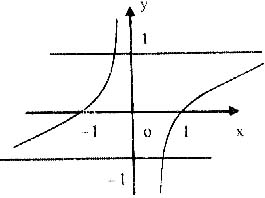
17.原方程化为![]()
令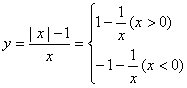
令y=a,它的图象为平行于x轴的直线
当a≥1时,两函数图象交点在y轴的左侧 ∴方程有一个负根无正根
当a≤-1时,两函数图象交点在y轴的右侧 ∴方程有一个正根无负根
当-1<a<1时,两函数图象交点在y轴的左右侧各有一个交点 ∴方程有一个正根一负根
综上:a≥1时原方程有一负根且没有正根
18.设f(x)=x2-2x+a, g(x)=x2-2bx+5
要使A![]() B则必须使f(x)与g(x)在[1,3]上的图象均在x轴下方(含x轴),则应满足
B则必须使f(x)与g(x)在[1,3]上的图象均在x轴下方(含x轴),则应满足
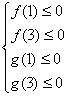 即
即 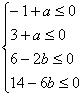 ∴a≤-3 b≥3
∴a≤-3 b≥3
19.∵an+an+1=-3n
∴an+2-an=(an+2+an+1)-(an+1+an)=-3(n+1)-(-3n)=-3
∴a1, a3,…, a2n+1和a2, a4, …, an都是公差为-3的等差数列
∴a52=a10+21(-3)=-80
a51=a11+20(-3)
∵a10+a11=-30 ∴a11=-13
∴a51=-73
b51=a51·a52=5840
20.(1)∵f(x)与g(x)图象关于直线x-1=0对称 ∴f(x)=g(2-x)
∴当x∈[-1,0]时,2-x∈[2,3]
∴f(x)=g(2-x)=-ax+2x3
又∵f(x)是偶函数 ∴x∈[0,1]时,-x∈[-1,0]
∴f(x)=f(-x)=ax-2x3
|
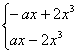
(2)f′(x)=a-6x2 ∵f(x)为[0,1]上的增函数 f′(x)=a-6x2≥0
∴a≥6x2在 x∈[0,1]上恒成立
∵x∈[0,1]时6x2≤6 ∴a>6 即a∈![]()
(3)∵f(x)为偶函数 ∴只需考虑x∈[0,1],由f′(x)=0
∴![]() 由
由![]() ∴a=6 此时x=1
∴a=6 此时x=1
∴当a∈(-6,6)时 f(x)最大值不可能为4
21.解:(1)设该店月利润余额为L,则由题设,得
L=Q(P-14)×100-3600-2000 ①
由销售图,易得:
Q=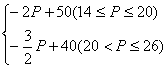
代入①式得,
L=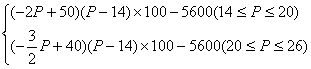
(1)当14≤P≤20时,由L≥0,得18≤P≤20,当20≤P≤26时,由L≥0,得20<P≤22
故商品销售价格应控制在18≤P≤22内
(2)18≤P≤20时,L最大=450(元),这时P=19.5元,当20≤P≤22时,L最大=416![]() (元),此时P=20
(元),此时P=20![]() 元,故当P=19.5元时,月利润余额最大为450元
元,故当P=19.5元时,月利润余额最大为450元
(3)设可在n年内脱贫,依题意,
有12n×450-50000-58000≥0,解得n≥20
即最早可望在20年后脱贫
22.(I)f(0)=f(0·0)=0·f(0)+0·f(0)=0
f(1)=f(1·1)=1·f(1)+1·f(1)
得f(1)=0
(II) f(x)是奇函数
证明:因为f(1)=f[(-1)2]=-f(-1)-f(-1)=0,所以f(-1)=0,
f(-x)=f(-1·x)=-f(x)+xf(-1)=-f(x)因此,f(x)为奇函数
(III)由f (a2)= af(a) + af (a)= 2af (a)
f (a3)= a2f (a) + af (a2)= 3a2f (a)
猜侧f (an)= nan-1f (a)
下面用数学归纳法证明:
①当n=1时,f (a1) =1·a0·f(a),公式成立;
②假设当n=k时,f(ak) =kak-1f(a)成立
那么当n=k+1时f (ak+1) =akf (a)+ af (ak)=akf (a)+kakf (a)
=(k+1)akf (a),公式仍成立
由上两步可知,对任意n∈N*, f (an)=nan-1f (a)成立
所以![]() =
=![]() , 因为f(2)=2,
, 因为f(2)=2,
f(1)=![]() 所以
所以![]()
![]() (n∈N*)
(n∈N*)
因此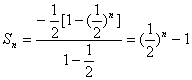 (n∈N*)
(n∈N*)