高三第二次月考数学试题
数学试题（文）
（总分：150分；时间：120分钟）
一、选择题:本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的．
1．设集合
,则A∩B等于(
)
A.
B. {2,4}
C.{(2,4),(4,16)} D. {4,16}
2．函数y =
在x =
1处的导数等于（ ）
（A）4 （B）－4 （C）3 （D）－3
3．函数
的定义域为（ ）
A．（1，3）B．
C．（1，2）∪（2，3） D．[1，3]
4．用反证法证明命题：“a，b∈N，ab可被5整除，那么a，b中至少有一个能被
5整除”时，假设的内容应为 （ ）
A. a，b都能被5整除 B. a，b都不能被5整除
C. a，b不都能被5整除 D. a不能被5整除
5．若函数f(x)=
, 则该函数在(-∞,+∞)上是
( )
A.单调递减无最小值 B.单调递减有最小值
C.单调递增无最大值 D.单调递增有最大值
6．已知直线
，则过P点的切线方程为 （ ）
A．
B．
C．
D．
7．已知函数
的图象与函数
的图象关于直线
对称，则
的值为（ ）
A．1 B．－1 C．2 D．－2
8．“
”是“
或
”的（
）
A．必要不充分条件 B．充分不必要条件 C．充要条件 D．既不充分也不必要条件
9．若不等式2x－3>4与不等式x2+px+q>0的解集相同，则p: q等于 （ ）
A．12：7 B．7：12 C．－12：7 D．－3：4
10．函数y=x+cosx的大致图象是
 |
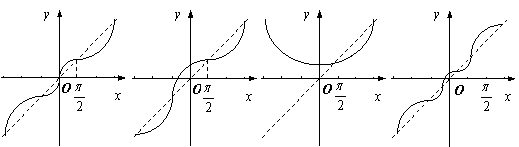11．某班由24名女生和36名男生组成，现要组织20名学生外出参观，若这20名学生按性别分层抽样产生，则参观团的组成方法共有（ ）
A．
种 B．
种 C．
种 D．
种
12．定义在R上的偶函数
，满足
，在区间［-2,0］上单调递减，设
，则
的大小顺序为( )
A.
B.
C.
D. 
二、填空题：本大题共4小题，每小题4分，共16分．把答案直接填在答题卷的相应题号的横线上.
13．已知函数
的最大值与最小值之差为4，则
.
14．若函数
的反函数的图象恒过P点，则P点坐标是
15．函数
的单调减区间为 .
16．定义在
上的奇函数
上为增函数，且
. 则不等式
的解集是
.
三、解答题（本大题共6小题，共74分. 解答应写出文字说明，证明过程或演算步骤，并把解答过程全部写在答题卷的相应题目指定的方框内.）
17. （本小题满分12分）已知集合
,B={x∣1<log2(x+1)<2}
若A∩B=A,求实数
的取值范围;
18．（本小题满分12分）设函数
的图象关于直线对称.
求
的值,并用定义判断
在
上的单调性;
19.（本小题满分12分）设P：关于x的不等式：
的解集是
.
Q：函数
的定义域为R. 如果P和Q有且仅有一个正确，求实数a的取值范围.
20.(本小题满分12分)
解关于x的不等式
（其中
）．
21．（本题满分12分）
设函数f(x)=x(x－1)x－a)(a>1).
（1）求导数f′(x)，并证明f(x)有两个不同的极值点x1、x2 ；
（2）若不等式f(x1)+f(x2)≤0成立，求a的取值范围.
22．（本小题满分14分）定义在
上的函数f (x)，对于任意的
，都有
成立，当
时，
.
（1）计算
；
（2）证明
在上是减函数；
（3）当
时，解不等式
.