高三第三次质量检测数学试卷
一、选择题(12小题,每题5分,共60分)
1、已知M={yy=x2},N={yx2+y2=2},则M![]() N=( )
N=( )
A、{(1,1),(-1,1)} B、{1} C、[0,1] D、[0,![]() ]
]
2、点P(2,-1)为圆 (x-1) 2+y2=25内弦AB中点,则直线AB的方程是( )
A、x-y-3=0 B、2x+y-3=0 C、x+y-1=0 D、2x-y-5=0
3、已知复数z与(z-2)2-![]() 均是纯虚数,则z =( )
均是纯虚数,则z =( )
A、![]() B、-
B、-![]() C、
C、![]() D、
D、![]()
4、点O在△ABC内部且满足![]() ,则△ABC面积与凹四边形ABOC面积之比是( )
,则△ABC面积与凹四边形ABOC面积之比是( )
A、0 B、![]() C、
C、![]() D、
D、![]()
5、函数![]() 在区间
在区间![]() 为减函数的充要条件是( )
为减函数的充要条件是( )
A、a≥0 B、a≤0 C、a>0 D、a<0
6、正四面体ABCD的棱长为1,G是底面△ABC的中心,M在线段DG上且使∠AMB=90°,则GM的长等于( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
7、已知函数![]() 图象上,相邻的一个最大值与一个最小值点恰好在
图象上,相邻的一个最大值与一个最小值点恰好在![]() 上,则f(x)最小正周期为( )
上,则f(x)最小正周期为( )
A. 1 B. 2 C. 3 D. 4
8、已知x、y满足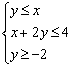 ,则S=x2+y2+2x-2y+2,最小值是( )
,则S=x2+y2+2x-2y+2,最小值是( )
A、![]() B、2
C、3 D、
B、2
C、3 D、![]()
9、(1-3x+2y)n展开式中不含y的项的系数和为( )
A、2n B、-2n C、(-2) n D、1
10、假设每一架飞机的引擎在飞行中出现故障率为1-p,且各引擎是否有故障是独立的,已知4引擎飞机中至少有3个引擎正常运行,飞机就可成功飞行;2引擎飞机要2个引擎全部正常运行,飞机也可成功飞行,要使4引擎飞机比2引擎飞机更安全,则P的取值范围是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
11、已知f(x)是R上的偶函数,对![]() 都有f(x+6)=f(x)+f(3)成立,若f(1)=2,则f(2005)=( )
都有f(x+6)=f(x)+f(3)成立,若f(1)=2,则f(2005)=( )
A、2005 B、2 C、1 D、0
12、在正三棱锥S-ABC中,M、N分别是棱SC、BC的中点,且MN⊥AM,若侧棱SA=![]() ,则此正三棱锥S-ABC外接球的表面积是( )
,则此正三棱锥S-ABC外接球的表面积是( )
A. 12π B. 32π C. 36π D. 48
二、填空题(4小题,每小题4分,共16分)
13、点P是抛物线y2=4x上一动点,则P到点(0,-1)的距离与P到直线x=-1的距离和的最小值是 。
14、![]() ,则a+b=
。
,则a+b=
。
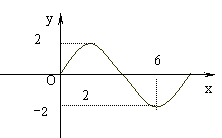 15、函数
15、函数![]() 的部分图象如图所示,则
的部分图象如图所示,则![]() _____________。
_____________。
16、方程f(x)=x的根称为f(x)的不动点,若函数![]() 有唯一不动点,且
有唯一不动点,且![]() ,
,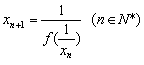 ,则
,则![]() 。
。
三、计算题(共74分)
17、(12分)已知点A(2,0),B(0,2),C(cos![]() ,sin
,sin![]() ),且0<
),且0<![]() <
<![]() 。
。
(1)若![]() ,求
,求![]() 与
与![]() 的夹角;
的夹角;
(2)若![]() ,求tan
,求tan![]() 的值。
的值。
18、(12分)已知函数![]() (x>1)
(x>1)
(1) 若函数在f(x)上是增函数,求实数p的取值范围;
(2) 解关于x的不等式f(x)<2.
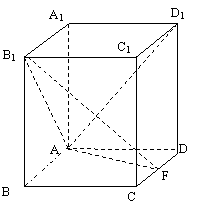
19、(12分)在棱长AB=AD=2,AA’=3的长方体AC1中,点E是平面BCC1B1上动点,点F是CD的中点。
(1)试确定E的位置,使D1E⊥平面AB1F。
(2)求二面角B1-AF-B的大小。
 |
20、(12分)如图,已知抛物线的方程为![]() ,过点M(0,m)且倾斜角为
,过点M(0,m)且倾斜角为![]() 的直线交抛物线于A(x1,y1),B(x2,y2)两点,且
的直线交抛物线于A(x1,y1),B(x2,y2)两点,且![]()
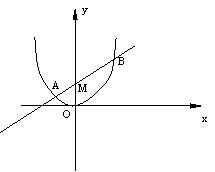 (1)求m的值
(1)求m的值
(2)若点M分![]() 所成的比为
所成的比为![]() ,求
,求![]() 关于
关于![]() 的函数关系式。
的函数关系式。
21、(12分)高二(1)班的一个研究性学习小组在网上查知,某珍稀植物种子在一定条件下发芽成功率为![]() ,该学习小组又分成两个小组进行验证性实验。
,该学习小组又分成两个小组进行验证性实验。
(1)第一小组做了5次这种植物种子的发芽实验(每次均种下一粒种子),求他们的实验至少有3次成功的概率。
(2)第二小组做了若干次发芽实验(每次均种下一粒种子),如果在一次实验中种子发芽成功就停止实验,否则将继续进行下去,直到种子发芽成功为止,但发芽实验的次数最多不超过4次,求第二个小组所做的种子发芽的实验次数![]() 的概率分布列和期望。
的概率分布列和期望。
22、(14分)过点P(1,0)作曲线![]() 的切线切点为Q1,设Q1点在x轴上的投影是点p1,又过点p1作曲线c的切线切点为Q2,设Q2在x轴上的投影是p2…,依此下去,得到一系列点Q1,Q2,…,Qn,…,设点Qn的横坐标为an
的切线切点为Q1,设Q1点在x轴上的投影是点p1,又过点p1作曲线c的切线切点为Q2,设Q2在x轴上的投影是p2…,依此下去,得到一系列点Q1,Q2,…,Qn,…,设点Qn的横坐标为an
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)求证:![]() (注:
(注:![]() )
)
高三第三次质量检测
1—5 D A A C A 6—10 D D B C B 11—12 B C
13、![]() 14、3 15、
14、3 15、![]() 16、2002
16、2002
17、解:∵(1),![]()
![]() ∴
∴![]()
又![]() ,∴
,∴![]()
又![]() ,∴
,∴![]() 与
与![]() 的夹角为
的夹角为![]() .
.![]() (5分)
(5分)
(2) ![]() ,
,![]()
∵![]() ,∴
,∴![]()
∴![]() ①
①
∴![]()
∴![]()
∵![]() ∴
∴![]()
又由![]() 及
及![]()
得![]() ②
②
由①②![]() ,
,![]()
∴![]() 。
。![]() (12分)
(12分)
18、解:(1) ![]() 在
在![]() 恒成立,则
恒成立,则
![]() 在
在![]() 恒成立,得
恒成立,得![]() 。
。![]() (6分)
(6分)
(2) 由![]() 及x>1得
及x>1得![]()
10.当p=-1时,![]() ,无解;
,无解;
20.当p>-1时,![]() 且x>1
且x>1
所以得1<x![]() .
.![]() (12分)
(12分)
19、解:(1)建立空间直角坐标系,如图
A(0,0,0),F(1,2,0),B1(2,0,3),D1(0,2,3),设E(2,y,z)
![]() ,
,![]() ,
,![]()
由D1E⊥平面AB1F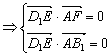 ,即
,即
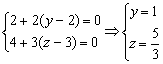
∴E(2,1,![]() )为所求。
)为所求。![]() (6分)
(6分)
(2)当D1E⊥平面AB1F时,![]() ,
,![]()
又![]() 与
与![]() 分别是平面BEF与平面B1EF的法向量,则
分别是平面BEF与平面B1EF的法向量,则
二面角B1-AF-B的平面角等于<![]() ,
,![]() >。
>。
∵cos<![]() ,
,![]() >=
>=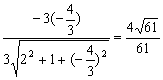
∴B1-AF-B的平面角为![]() 或用传统法做(略) (
或用传统法做(略) (![]() )
)![]() (12分)
(12分)
20、①设AB方程为y=kx+m代入x2=2py得
![]() ①
①
由![]() 得
-2pm=-p2
得
-2pm=-p2
∴2m=p,即![]() ……………………(6分)
……………………(6分)
②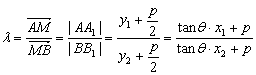
由①得![]()
![]()
∴![]()
![]() …………………………(12分)
…………………………(12分)
21、解:(1)这5次实验是独立,则至少有3次成功的概率是
![]()
![]() (6分)
(6分)
(2) ![]() 1 2
3
4
1 2
3
4
P ![]()
![]()
![]()
![]()
E![]() =
=![]()
![]()
![]() (12分)
(12分)
22、
(1)![]() ,若切点是Qn(an,ank),则切线方程是
,若切点是Qn(an,ank),则切线方程是![]()
当n=1时,切线过点P(1,0)
即![]() ,得
,得![]() ;当n>1时,切线过点
;当n>1时,切线过点![]()
即![]()
得![]()
所以数列![]()
![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,
的等比数列,![]() ,
,![]() (4分)
(4分)
(2)![]()
![]()
![]() ………………………………(8分)
………………………………(8分)
(3)设![]()
则![]() 两式相减,得
两式相减,得
![]() ,
,
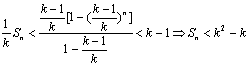 ………………………………(14分)
………………………………(14分)