高三第一次调研考试数学试题2
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
⒈已知全集![]() ,集合
,集合![]() ,
,![]() ,则
,则![]() 为
为
A.![]() B.
B.![]()
C.![]() D.
D.![]()
⒉设0<a<1,实数x,y满足x+![]() =0,则y关于x的函数的图象大致形状是
=0,则y关于x的函数的图象大致形状是
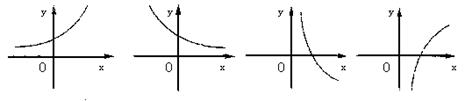
A B C D
⒊条件![]() ,条件
,条件![]() ,则
,则![]() 是
是![]() 的
的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
⒋已知△ABC的三个顶点A、B、C及其所在平面内一点P,满足![]() ,则点P与△ABC的关系为
,则点P与△ABC的关系为
A. P在△ABC内部 B. P在△ABC外部
C. P在边AB所在的直线上 D. P是AC边的一个三等分点
⒌设![]() ,则下列不等式成立的是
,则下列不等式成立的是
A.![]() B.
B.![]()
![]()
C.![]() D.
D.![]()
⒍将奇函数![]() 的图象沿x轴的正方向平移2个单位,所得的图象为C,又设图象
的图象沿x轴的正方向平移2个单位,所得的图象为C,又设图象![]() 与C关于原点对称,则
与C关于原点对称,则![]() 对应的函数为
对应的函数为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
⒎函数![]() 是
是
A.最小正周期为2π的奇函数 B.最小正周期为2π的偶函数
C.最小正周期为π的奇函数 D.最小正周期为π的偶函数
⒏(文)设A、B是锐角三角形ABC的两个内角,则有
A.![]() B.
B.![]()
C.![]() D.
D.![]()
(理)已知![]() ,
,![]() 的最大值为a,最小值为b,
的最大值为a,最小值为b,![]() 的最大值为c,最小值为d,则a、b、c、d从小到大的顺序为
的最大值为c,最小值为d,则a、b、c、d从小到大的顺序为
A.b<d<a<c B.d<b<c<a C.b<d<c<a D.d<b<a<c
⒐计算机是将信息转换成二进制进行处理的,所谓二进制即“逢二进一”,如(1101)2表示二进制的数,将它转换成十进制数的形式是1×23+1×22+0×21+1×20=13,那么将二进制数![]() 转换成十进制数是
转换成十进制数是
A.217-2 B.216-1 C.216-2 D.215-1
⒑(文)若函数![]() 的定义域为
的定义域为![]() ,则实数a的取值范围是
,则实数a的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(理)不等式![]() 在
在![]() 上恒成立,则实数a的取值范围是
上恒成立,则实数a的取值范围是
A.[2,+![]() B.
B.![]() C.
C.![]() D.
D.![]()
⒒某地每年消耗木材约20万![]() ,每
,每![]() 价480元,为了减少木材消耗,决定按
价480元,为了减少木材消耗,决定按![]() 征收木材税,这样每年的木材消耗量减少
征收木材税,这样每年的木材消耗量减少![]() 万
万![]() ,为了既减少木材消耗又保证税金收入每年不少于180万元,则
,为了既减少木材消耗又保证税金收入每年不少于180万元,则![]() 的范围是
的范围是
A.[1,3] B.[2,4] C.[3,5] D.[4,6]
⒓已知数列![]() 满足
满足![]()
![]() ,
,![]() ,
,![]() ,设
,设![]() ,则下列结论正确的是
,则下列结论正确的是
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
⒔在△ABC中,已知![]() ,a、b、c分别为角A、B、C所对的边,则
,a、b、c分别为角A、B、C所对的边,则![]() 的值等于
.
的值等于
.
⒕(文)等差数列![]() 中,
中,![]() ,公差不为零,且
,公差不为零,且![]() 、
、![]() 、
、![]() 恰好成等比数列,那么该等比数列公比的值等于 .
恰好成等比数列,那么该等比数列公比的值等于 .
(理)等比数列![]() 中,
中,![]() ,公比
,公比![]() ,用
,用![]() 表示它的前n项之积:
表示它的前n项之积:
![]() ,则
,则![]() ,
,![]() ,…中最大的是
.
,…中最大的是
.
⒖光线透过一块玻璃板,其强度要减弱![]() ,要使光线的强度减弱到原来的
,要使光线的强度减弱到原来的![]() 以下,至少有这样的玻璃板 块;(参考数据:
以下,至少有这样的玻璃板 块;(参考数据:![]()
⒗给出下列四个命题:
① 函数![]() 为奇函数的充要条件是
为奇函数的充要条件是![]() =0;
=0;
②函数![]() 的反函数是
的反函数是![]() ;
;
③若函数![]() 的值域是R,则
的值域是R,则![]() 或
或![]() ;
;
④ 若函数![]() 是偶函数,则函数
是偶函数,则函数![]() 的图象关于直线
的图象关于直线![]() 对称。其中所有正确命题的序号是
.
对称。其中所有正确命题的序号是
.
三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
⒘(本小题满分12分)
已知函数![]()
(Ⅰ)求![]() 的最小正周期;
的最小正周期;
(Ⅱ)求![]() 的单调递减区间;
的单调递减区间;
(Ⅲ)函数![]() 的图象经过怎样的平移才能使所得图象对应的函数成为奇函数?
的图象经过怎样的平移才能使所得图象对应的函数成为奇函数?
⒙(本小题满分12分)
已知:![]() 、
、![]() 、
、![]() 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中![]() =(1,2)
=(1,2)
(Ⅰ)若![]()
![]() ,且
,且![]() //
//![]() ,求
,求![]() 的坐标;
的坐标;
(Ⅱ)若![]() =
=![]() 且
且![]() 与
与![]() 垂直,求
垂直,求![]() 与
与![]() 的夹角θ.
的夹角θ.
⒚(本小题满分12分)
(文)解不等式![]() .
.
(理)是否存在常数c,使得不等式![]() 对任意正实数x、y恒成立?证明你的结论.
对任意正实数x、y恒成立?证明你的结论.
⒛(本小题满分12分)
已知函数![]() .
.
(Ⅰ)求函数![]() 的定义域;
的定义域;
(Ⅱ)若函数![]() 在[10,+∞)上单调递增,求k的取值范围.
在[10,+∞)上单调递增,求k的取值范围.
21.(本小题满分12分)
一列火车自A城驶往B城,沿途有n个车站(包括起点站A和终点站B),车上有一节邮政车厢,每停靠一站便要卸下前面各站发往该站的邮袋各一个,同时又要装上该站发往后面各站的邮袋各一个,试求:
(1)列车从第k站出发时,邮政车厢内共有邮袋数是多少个?
(2)第几站的邮袋数最多?最多是多少?
22.(本小题满分14分)
已知![]()
(Ⅰ)若![]() 能表示成一个奇函数
能表示成一个奇函数![]() 和一个偶函数
和一个偶函数![]() 的和,求
的和,求![]() 和
和![]()
的解析式;
(Ⅱ)若![]() 和
和![]() 在区间
在区间![]() 上都是减函数,求a的取值范
上都是减函数,求a的取值范
(Ⅲ)在(Ⅱ)的条件下,比较![]() 的大小.
的大小.
高三第一次调研考试
数学试题答案及评分标准
一、选择题:每小题5分,共60分.
CAABC DCAAC CB
二、填空题:每小题4分,共16分.
⒔1 ⒕(文)4(理)![]() ⒖11;
⒗①②③
⒖11;
⒗①②③
三、⒘(Ⅰ)由![]()
由![]() ……2分
……2分
![]() ……6分
……6分
∴函数![]() 的最小正周期T=
的最小正周期T=![]() ……7分
……7分
(Ⅱ)由![]()
∴![]() 的单调递减区间是
的单调递减区间是![]()
![]() .
……10分
.
……10分
(Ⅲ)![]() ,
,
∴奇函数![]() 的图象左移
的图象左移![]() 即得到
即得到![]() 的图象,
的图象,
故函数![]() 的图象右移
的图象右移![]() 个单位后对应的函数成为奇函数.
……12分
个单位后对应的函数成为奇函数.
……12分
(注:第Ⅲ问答案不唯一)
⒙(Ⅰ)设![]()
![]()
![]() ……3分
……3分
由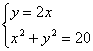 得
得 ![]() 或
或 ![]()
∴![]() ……5分
……5分
(Ⅱ)![]() ……6分
……6分
![]() ……(※)
……(※)
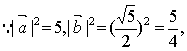 代入(※)中,
代入(※)中,
![]() ……9分
……9分
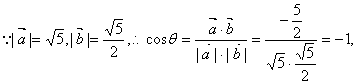
![]() ……12分
……12分
⒚(文)原不等式等价于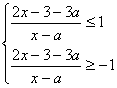 ,
……2分
,
……2分
移项,通分得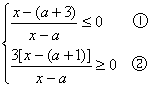 ……6分
……6分
由已知![]() ,所以解①得
,所以解①得 ![]() ,
,
解②得 ![]() 或
或![]() ……10分
……10分
故原不等式的解集为![]() ……12分
……12分
(理)当![]() 时,由已知不等式得
时,由已知不等式得![]() ……3分
……3分
下面分两部分给出证明:
⑴先证![]() ,
,
此不等式![]()
![]()
![]() ,此式显然成立;
……7分
,此式显然成立;
……7分
⑵再证![]() ,
,
此不等式![]()
![]()
![]() ,此式显然成立.
……10分
,此式显然成立.
……10分
综上可知,存在常数![]() ,是对任意的整数x、y,题中的不等式成立.…12分
,是对任意的整数x、y,题中的不等式成立.…12分
⒛(Ⅰ)由 ……1分
……1分
(1)当0<k<1时,得![]() ; ……2分
; ……2分
(2)当k=1时,得![]() ……3分
……3分
(3)当k>1时,得![]() ……4分
……4分
综上,
当0<k<1时,函数的定义域为![]() ;
;
当![]() 时,函数的定义域为
时,函数的定义域为![]() ……6分
……6分
(Ⅱ)由![]() 上是增函数
上是增函数 ![]() ……8分
……8分
又![]() ,故对任意的
,故对任意的![]() 、
、![]() ,当
,当![]() 时,
时,
有![]() 得:
得:
![]()
又![]() ……11分
……11分
综上可知k的取值是(![]() )……………………………………………………12分
)……………………………………………………12分
(注:第Ⅱ问也可用求导的方法求解.)
21. 设列车从各站出发时邮政车厢内的邮袋数构成一个数列![]()
(1)由题意得:
![]() ……2分
……2分
在第k站出发时,前面放上的邮袋共:![]() 个 ……4分
个 ……4分
而从第二站起,每站放下的邮袋共:1+2+3+…+(k-1)个 ……6分
故![]()
![]()
即列车从第k站出发时,邮政车厢内共有邮袋数![]() 个 ……8分
个 ……8分
(2)![]() 当n为偶数时,
当n为偶数时,![]() 时,最大值为
时,最大值为![]()
当n为奇数时,![]() 时,最大值为
时,最大值为![]() .
.
所以,当n为偶数时,第![]() 站的邮袋数最多,最多是
站的邮袋数最多,最多是![]() 个;
个;
当n为奇数时,第![]() 站的邮袋数最多,最多是
站的邮袋数最多,最多是![]() 个 ……12分
个 ……12分
22.(Ⅰ)设![]() ①,其中
①,其中![]() 是奇函数,
是奇函数,![]() 是偶函数,
是偶函数,
则有 ![]() ②
②
联立①,②可得
![]() ,
,![]() (直接给出这两个函数也给分)…3分
(直接给出这两个函数也给分)…3分
(Ⅱ)函数![]() 当且仅当
当且仅当 ![]() ,即
,即![]() 时才是减函数,
时才是减函数,
∴![]()
又![]()
∴![]() 的递减区间是
的递减区间是 ![]() ……5分
……5分
由已知得![]()
∴ 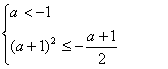
解得![]()
∴![]() 取值范围是
取值范围是![]() ……8分
……8分
(Ⅲ)![]()
![]() 在
在![]() 上为增函数 ……10分
上为增函数 ……10分
∴![]()
![]()
∴![]() 即
即![]() . ……14分
. ……14分