高考数学联考试卷
一.选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设全集U=R,![]()
![]() B)是
B)是
A.![]() B.
B.![]() 或
或![]()
C.![]() D.
D.![]()
2.若函数f(x)同时具有以下两个性质:①f(x)是偶函数,②对任意实数x,都有f(![]() )= f(
)= f(![]() ),则f(x)的解析式可以是
),则f(x)的解析式可以是
A.f(x)=cosx B.f(x)=cos(2x![]() ) C.f(x)=sin(4x
) C.f(x)=sin(4x![]() ) D.f(x) =cos6x
) D.f(x) =cos6x
3.已知等比数列![]() 中,
中,![]() 为方程
为方程![]() 的两根,则
的两根,则![]() 的值为
的值为
A.32 B.64 C.256 D.±64
4.对于直线m,n和平面![]() ,
,![]() ,
,![]() ⊥
⊥![]() 的一个充分条件是
的一个充分条件是
A.m⊥n,m∥![]() ,n∥
,n∥![]() B.m⊥n,
B.m⊥n,![]() ∩
∩![]() =m,n
=m,n![]()
![]()
C.m∥n,n⊥![]() ,m
,m![]()
![]() D.m∥n,m⊥
D.m∥n,m⊥![]() ,n⊥
,n⊥![]()
5.椭圆的焦点为F1、 F2,过点F1作直线与椭圆相交, 被椭圆截得的最短的线段MN长为![]() ,
,
![]() 的周长为20, 则椭圆的离心率为
的周长为20, 则椭圆的离心率为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
6、某餐厅供应客饭,每位顾客可以在餐厅提供的菜肴中任选2荤2素共4种不同的品种,现在餐厅准备了五种不同的荤菜,若要保证每位顾客有200种以上不同选择,则餐厅至少还需准备不同的素菜品种
A、10 B、9 C、8 D、7
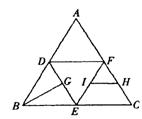 7.如图,在正三角形ABC中,D、E、F分别为各边的中点,G、H、I分别为DE、FC、EF的中点,将△ABC沿DE、EF、DF折成三棱锥以后,BG与IH所成的角的弧度数为
7.如图,在正三角形ABC中,D、E、F分别为各边的中点,G、H、I分别为DE、FC、EF的中点,将△ABC沿DE、EF、DF折成三棱锥以后,BG与IH所成的角的弧度数为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.若一系列函数的解析式相同,值域相同,但其定义域不同,则称这些函数为“同族函数”,那么函数解析式为![]() ,值域为
,值域为![]() 的“同族函数”共有
的“同族函数”共有
A.9个 B.8个 C.5个 D.4个
9.将函数 y = cos x-sin x 的图象向左平移 m(m > 0)个单位,所得到的图象关于 y 轴对称,则 m 的最小正值是
A. B. C. D.
10.下列同时满足条件:
(1)是奇函数(2)在![]() 上是增函数(3)在
上是增函数(3)在![]() 上最小值为0的函数是
上最小值为0的函数是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11 过圆![]() +
+![]() -4x=0外一点P(m,n)作圆的两条切线,当这两条切线互相垂直时,m,n 应满足的关系式为
-4x=0外一点P(m,n)作圆的两条切线,当这两条切线互相垂直时,m,n 应满足的关系式为
A. ![]() +
+ ![]() =4
B.
=4
B. ![]() +
+![]() =4
=4
C. ![]() +
+ ![]() =8
D.
=8
D. ![]() +
+![]() =8
=8
12.常州某中学的研究性学习小组为考察天目湖地区的一个小岛的湿地开发情况,从某码头乘汽艇出发,沿直线方向匀速开往该岛,靠近岛时,绕小岛环行两周后,把汽艇停靠岸边上岸考察,然后又乘汽艇沿原航线匀速返回。设t为出发后的某一时刻,S为汽艇与码头在时刻t的距离,下列图象中能大致表示S=f(x)的函数关系的为
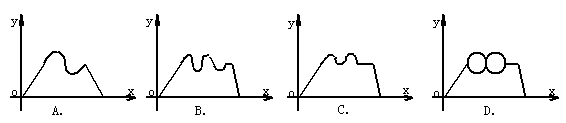
二.填空题:本大题共有4小题,每小题3分,共12分.把答案填在题中横线上.
13.球面上有A、B、C三点,AB=AC=2,BC=2![]() ,球心到平面ABC的距离为1,则球的表面积为
,球心到平面ABC的距离为1,则球的表面积为
14. 已知![]() 的展开式中的常数项是第七项, 则正整数n的值为
.
的展开式中的常数项是第七项, 则正整数n的值为
.
15.直线![]() 过椭圆
过椭圆![]() 的一个焦点,则b的值是
的一个焦点,则b的值是
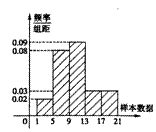 16.右图是一个容量为200的样本的频率分布直方图,请根据图形中
16.右图是一个容量为200的样本的频率分布直方图,请根据图形中
的数据填空:
(1)样本数据落在范围![]() 的频率为
;
的频率为
;
(2)样本数据落在范围![]() 的频数为
;
的频数为
;
三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)设![]() ,
,![]() 是平面内两个向量
是平面内两个向量
⑴ 若![]() 且
且![]() ,求
,求![]() ;
;
⑵ 若![]() ,求
,求![]() .
.
18.(本小题满分12分)
袋子里有大小相同但标有不同号码的3个红球和4个黑球,从袋子里随机取球,设取到一个红球得2分,取到一个黑球得1分。
(Ⅰ)若从袋子里随机取出4个球,求得5分的概率;
(Ⅱ)若从袋子里每次摸出一个球后,看清颜色后放回,求连续4次摸球共得5分的概率。
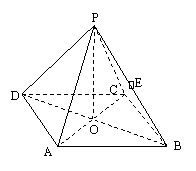 19.(本小题满分12分)如图所示,正四棱锥
19.(本小题满分12分)如图所示,正四棱锥![]() 中,侧棱
中,侧棱![]() 与底面
与底面![]() 所成的角的正切值为
所成的角的正切值为![]() .
.
(1)求侧面![]() 与底面
与底面![]() 所成的二面角的大小;
所成的二面角的大小;
(2)若![]() 是
是![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成角的正切值;
所成角的正切值;
(3)问在棱AD上是否存在一点![]() ,使
,使![]() ⊥侧面
⊥侧面![]() ,若存在,试确定点
,若存在,试确定点![]() 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
20.(本小题满分12分)
已知两个函数![]() ,
,![]() .
.
(Ⅰ)若对任意![]() [-3,3],都有
[-3,3],都有![]() ≤
≤![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若对任意![]() [-3,3],
[-3,3],![]() [-3,3],都有
[-3,3],都有![]() ≤
≤![]() 成立,求实数
成立,求实数![]() 的取值范围。
的取值范围。
21.(本小题满分12分)
已知数列![]() 的前
的前![]() 项和
项和![]() 满足
满足![]()
(Ⅰ)求k的值;
(Ⅱ)求![]() ;
;
(Ⅲ)是否存在正整数![]() 使
使![]() 成立?若存在求出这样的正整数;若不存在,说明理由
成立?若存在求出这样的正整数;若不存在,说明理由
22.(本小题满分14分)
在平面直角坐标系中,![]() 为坐标原点,已知两点
为坐标原点,已知两点![]() 、
、![]() ,若点
,若点![]() 满足
满足![]() (
(![]() ),点
),点![]() 的轨迹与抛物线:
的轨迹与抛物线:![]() 交于
交于![]() 、
、![]() 两点.
两点.
(Ⅰ)求证:![]() ⊥
⊥![]() ;
;
(Ⅱ)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得过点
,使得过点![]() 直线交抛物线于D、E两点,并以该弦DE为直径的圆都过原点。若存在,请求出
直线交抛物线于D、E两点,并以该弦DE为直径的圆都过原点。若存在,请求出![]() 的值及圆心的轨迹方程;若不存在,请说明理由.
的值及圆心的轨迹方程;若不存在,请说明理由.
联考试卷参考答案
一、选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | C | D | C | B | D | A | A | D | B | C | C |
二、填空题:
13. ![]() 14. 8 15.
14. 8 15. ![]() 16. 0.32 72
16. 0.32 72
17:解:⑴![]() 或
或![]() . 6分
. 6分
⑵![]()
![]() 12分
12分
18:(1)要得到5分,则取到3个黑球、一个红球,
从袋子里随机取出4个球,得5分记为事件A,则![]()
答:从袋子里随机取出4个球,得5分的概率![]() 6分
6分
(2)从袋子里每次摸出一个球后,放回4次摸球共得5分记为事件B,根据独立重复事件可得:
![]()
答:从袋子里每次摸出一个球后,放回,4次摸球共得5分的概率为![]() 12分
12分
19. 解:(1)取![]() 中点
中点![]() ,设
,设![]() ,连
,连![]() 、
、![]() ,则
,则![]() 为二面角的平面角,
为二面角的平面角,![]() 为侧棱
为侧棱![]() 与底面
与底面![]() 所成的角,
所成的角,![]() ,设
,设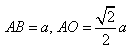 ,
,![]() ,
,![]()
∴∠PMO=60°. 4分
(2)连![]() ,
,![]() ∥
∥![]() ,
,![]() 为异面直线
为异面直线![]() 与
与![]() 所成的角.
所成的角.
 . ∵
. ∵![]() ∴
∴![]() ……8分
……8分
3)延长![]() 交
交![]() 于
于![]() ,取
,取![]() 中点
中点![]() ,连
,连![]() 、
、![]() .
.
![]() .又
.又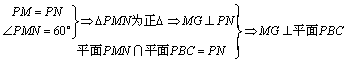
取![]() 中点
中点![]() ,∵
,∵![]() ∥
∥![]() ∴
∴![]() ∴
∴![]() ∥
∥![]() .∴
.∴![]() 平面
平面![]() .即F为四等分点………
12分
.即F为四等分点………
12分
21.解:(I)![]()
又![]() ………………2分
………………2分
(Ⅱ)由(I)知![]() ①
①
当![]() 时,
时,![]() ②
②
①-②,得![]() ………………4分
………………4分
又![]() ,易见
,易见![]()
于是![]() 是等比数列,公比为
是等比数列,公比为![]() ,所以
,所以
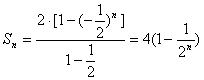 ………………6分
………………6分
(Ⅲ)不等式![]() ,即
,即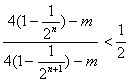
整理得![]() …………8分
…………8分
假设存在正整数![]() 使得上面的不等式成立,由于2n为偶数,
使得上面的不等式成立,由于2n为偶数,![]() 为整数,则只能是
为整数,则只能是![]()
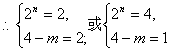 ………………10分
………………10分
因此,存在正整数![]() …………12
…………12
(22)解:1)解:由![]() (
(![]() )知点
)知点![]() 的轨迹是
的轨迹是![]() 、
、![]() 两点所在的直线,故 点
两点所在的直线,故 点![]() 的轨迹方程是:
的轨迹方程是:![]() 即
即![]() ………… ….2分
………… ….2分
由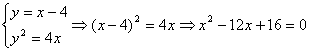
∴![]()
![]()
∴![]()
∴![]() 故
故 ![]() ⊥
⊥![]() . ……………………………………6分
. ……………………………………6分
2)解:存在点![]() ,使得过点
,使得过点![]() 任作抛物线的一条弦,以该弦为直径的圆都过原点
任作抛物线的一条弦,以该弦为直径的圆都过原点
由题意知:弦所在的直线的斜率不为零 …………………………………7分
故 设弦所在的直线方程为:![]() 代入
代入 ![]() 得
得 ![]()
∴ ![]()
![]()
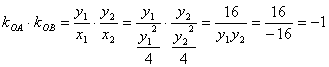
∴![]() 故以
故以![]() 为直径的圆都过原点 …………………………..10分
为直径的圆都过原点 …………………………..10分
设弦![]() 的中点为
的中点为![]() 则
则![]()
![]()
![]()
∴弦![]() 的中点
的中点![]() 的轨迹方程为:
的轨迹方程为:
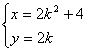 消去
消去![]() 得
得 ![]() . ……………………14分
. ……………………14分