高考数学模拟冲刺卷(A)
(内部资料,注意保密)
(试卷总分:150分 考试时间:120分钟)
第Ⅰ卷(选择题,共60分)
一、 选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.已知x∈( -![]() , 0 ),cosx=
, 0 ),cosx=![]() ,则tan2x=
( )
,则tan2x=
( )
A.![]()
B.-
B.-![]() C.
C.![]() D-
D-![]()
答案:C(提示:由cosx=![]() ,x∈( -
,x∈( -![]() , 0 ), 得sinx= -
, 0 ), 得sinx= -![]() ,∴tanx= -
,∴tanx= -![]() ,∴tan2x=
,∴tan2x=![]() =
=![]() ,选C)
,选C)
2.设集合M={x|x2-x<0,x∈R![]() ,N={x||x|<2,x∈R
,N={x||x|<2,x∈R![]() ,则
( )
,则
( )
A. N ![]() M B. M∩N=M C. M∪N=M D. M∪N=R
M B. M∩N=M C. M∪N=M D. M∪N=R
答案:B(提示:M={x|0<x<1﹜,N={x|-2<x<2﹜,∴M∩N=M,选B![]()
3. 已知多项式16x4+32x3+24x2+8x+1能被5整除,则满足条件的最小自然数x的值为( )
A. 7 B. 4 C. 2 D. 1
答案:C(提示:16x4+32x3+24x2+8x+1=(2x+1)4,显然x=2满足题中条件,选C)
4. 已知一个简单多面体的各个面都是三角形,则顶点数V与面数F满足的关系是 ( )
A. 2V-F=4 B. 2V+F=4 C. 2V+F=2 D. 2V-F=2
答案:A(提示:由欧拉公式得V+F-E=2,又由3F=2E解得E=![]() F代入前一式得2V-F=4,选A)
F代入前一式得2V-F=4,选A)
5. 一动圆圆心在抛物线x2=2y上,过点(0,![]() )且恒与定直线l相切,则直线l的方程( )
)且恒与定直线l相切,则直线l的方程( )
A. x=![]() B. x=
B. x=![]() C. y= -
C. y= -![]() D.
y= -
D.
y= -![]()
答案:C(提示:抛物线x2=2y的焦点坐标为(0, ![]() ), 由抛物线的定义知抛物线上任意一点到焦点F(0,
), 由抛物线的定义知抛物线上任意一点到焦点F(0, ![]() )的距离等于到直线y=-
)的距离等于到直线y=-![]() 的距离,故选C)
的距离,故选C)
6. 已知![]() ,
, ![]() ,
,![]() 为任意非零向量,有下列命题:①|
为任意非零向量,有下列命题:①|![]() |=|
|=|![]() |,②
|,②![]() 2=
2=![]() 2,
2,
③![]() ·(
·(![]() -
- ![]() )=0,其中可作为
)=0,其中可作为![]() =
=![]() 的必要不充分的条件是
( )
的必要不充分的条件是
( )
A. ①② B.②③ C. ①②③ D. ①
答案:C(提示:由 ![]() =
=![]() 能推导出①、②、③成立,但|
能推导出①、②、③成立,但|![]() |=|
|=|![]() |,
|, ![]() 2=
2=![]() 2由于方向不一定同向,故不能推出
2由于方向不一定同向,故不能推出![]() =
=![]() ; 只要
; 只要![]() 与
与![]() -
- ![]() 垂直就有
垂直就有![]() ·(
·(![]() -
-![]() )=0,也不一定推出
)=0,也不一定推出![]() =
=![]() ,所以①、②、③都是
,所以①、②、③都是![]() =
=![]() 的必要不充分条件,选C)
的必要不充分条件,选C)
7. 已知a,b,c是空间三条直线,α、β是两个平面,下列命题中不正确的是 ( )
A. 若a∥b,b∥α,则a∥α或a![]() α
α
B. 若a⊥α,b⊥β,α∥β,则a∥b
C. 若a∥b,α∥β,则a与α所成角等于b与β所成的角
D. 若a⊥b,a⊥c,则b∥c
答案:D(提示:当a⊥b,b⊥c时,b与c可以是异面、平行或相交,选D)
8. (理)一个正整数数表如下(表中下一行中的数的个数是上一行中数的个数的2倍):
| 第1行 | 1 |
| 第2行 | 2 3 |
| 第3行 | 4 5 6 7 |
| … | … |
则第9行中的第4个数是 ( )
A. 132 B. 255 C. 259 D. 260
答案:C(提示:由数表知表中各行数的个数构成一个以1为首项,公比为2的等比数列,前8行数的个数共有![]() =255个,故第9行中的第4个数是259,选C)
=255个,故第9行中的第4个数是259,选C)
8.(文)将数列{3n-1}按“第n组有n个数”的规则分组如下:(1),(3,9),(27,81,243),…,则第100组中的第一个数是 ( )
A.34950 B.35000 C. 35010 D.35050
答案:A(提示:由“第n组有n个数”的规则分组中,各组数的个数构成一个以1为首项,公差为1的等差数列,前99组数的个数共有![]() =4950个,故第100组中的第1个数是34950,选A)
=4950个,故第100组中的第1个数是34950,选A)
9. 两条直径把圆面分成为四部分(如右图),现用4种颜色涂这四个区域,相邻区域不同色的涂法共有( )种 ( )
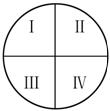 A. 32 B. 84 C. 86 D.
88
A. 32 B. 84 C. 86 D.
88
答案:B(提示:法一 分三类:用四种颜色去涂有A![]() =24;用三种颜色去涂,则相对的两个区域涂同一色,于是有C
=24;用三种颜色去涂,则相对的两个区域涂同一色,于是有C![]() ×C
×C![]() ×C
×C![]() ×A
×A![]() =48;用两种颜色去涂有C
=48;用两种颜色去涂有C![]() ×A
×A![]() =12;所以总共有24+48+12=84种,选B
=12;所以总共有24+48+12=84种,选B
法二 分两类:Ⅰ号与Ⅳ号区域涂同一色有C![]() ×C
×C![]() ×C
×C![]() =36;Ⅰ号与Ⅳ号区域涂不同色有C
=36;Ⅰ号与Ⅳ号区域涂不同色有C![]() ×A
×A![]() ×C
×C![]() ×C
×C![]() =48;所以总共有84种,选B)
=48;所以总共有84种,选B)
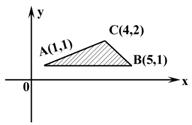
10. 在如图所示的坐标平面的可行域内(阴影部分且包括周界),目标函效z=2x-ay取得最大值的最优解有无数个,则a的一个可能值为
( )
A. –2 B. 2 C. –6 D. 6
答案:A(提示:要使目标函数z=2x-ay取得最值的最优解有无数个,则必须直线2x-ay-z=0与可行域边界线段AB或BC或AC重合,显然不可能与AB重合,由斜率有![]() =
=![]() 或-1得a=6或a=-2. 当a=6时,直线2x-ay-z=0与AC重合,此时z有最小值-4;当a=-2时,直线2x-ay-z=0与BC重合,此时z有最大值12,选A)
或-1得a=6或a=-2. 当a=6时,直线2x-ay-z=0与AC重合,此时z有最小值-4;当a=-2时,直线2x-ay-z=0与BC重合,此时z有最大值12,选A)
11. 已知O为ΔABC所在平面内一点,满足|![]() |2+|
|2+|![]() |2=|
|2=|![]() |2+|
|2+|![]() |2=
|2=
|![]() |2+|
|2+|![]() |2,则点O是ΔABC的
( )
|2,则点O是ΔABC的
( )
A. 外心 B. 内心 C. 垂心 D. 重心
答案:C(提示:由|![]() |2+|
|2+|![]() |2=|
|2=|![]() |2+|
|2+|![]() |2=|
|2=|![]() |2+|
|2+|![]() |2,得
|2,得![]() 2+(
2+(![]() -
-![]() )2=
)2=![]() 2+(
2+(![]() -
-![]() )2,
)2, ![]() ·
·![]() =
=![]() ·
·![]() ,即(
,即(![]() -
-![]() )·
)·![]() =0,即
=0,即![]() ·
·![]() =0,故
=0,故![]() ⊥
⊥![]() ,同理
,同理![]() ⊥
⊥![]() ,
, ![]() ⊥
⊥![]() ,故O是ΔABC的垂心,选C)
,故O是ΔABC的垂心,选C)
12. (理)设A为双曲线![]() -
-![]() =1右支上一动点,F为该双曲线的右焦点,连AF交双曲线于B,过B作直线BC垂直于双曲线的右准线,垂足为C,则直线AC必以过定点
( )
=1右支上一动点,F为该双曲线的右焦点,连AF交双曲线于B,过B作直线BC垂直于双曲线的右准线,垂足为C,则直线AC必以过定点
( )
A. (![]() ,0)
B. (
,0)
B. (![]() ,0)
,0)
C.
(4, 0 )
D. (![]() , 0 )
, 0 )
答案:A(提示:考虑特殊情况,设右准线与x轴交于E,则AC必过EF的中点,可用相似三角形知识结合双曲线定义证,选A)
12.(文)已知P是椭圆![]() +
+![]() =1上的一点,Q、R分别是圆(x+4)2+y2=
=1上的一点,Q、R分别是圆(x+4)2+y2=![]() 和(x-4)2+y2=
和(x-4)2+y2=![]() 上的点,则PQ+PR的最小值是
( )
上的点,则PQ+PR的最小值是
( )
A.![]() B.
B.![]() C.10
D.9
C.10
D.9
答案:D(提示:设椭圆的焦点为F1、F2,恰为两圆的圆心,则PQ+PR的最小值转化为P到F1、F2的距离之和达到最小问题,因PF1+PF2=10,故PQ+PR的最小值为9,选D)
第Ⅱ卷(选择题,共90分)
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上
13. 若曲线f(x)=x4-x在点P处的切线平行于直线3x-y=0,则点P的坐标为______________
答案:(1,0)(提示:设P(x0,y0),k=f′(x0)=4x3-1|x=x0=4x03-1=3,得x0=1,代入曲线方程f(x)=x4-x,得y0=0,填(1,0))
14. (理)一个正方体的全面积为a2,它的顶点都在同一个球面上,则这个球的体积为_________
答案:![]() πa3(提示:设正方体的边长为x,球的半径为R,解6x2=a2,∴x=
πa3(提示:设正方体的边长为x,球的半径为R,解6x2=a2,∴x=![]() a,由
a,由![]() x=2R,得R=
x=2R,得R=![]() x=
x=![]() a,∴球体积为
a,∴球体积为![]() πR3=
πR3=![]() πa3,填
πa3,填![]() πa3)
πa3)
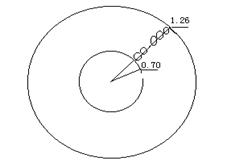
14.(文)如图,一个电缆盘上缠绕着直径为8cm的通讯电缆,空盘时,盘芯半径为0.70m,满盘时半径为1.26m,盘宽为1.44m,则满盘时,电缆盘上的电缆长度估计为___m,[假设电缆缠绕时构成同心圆,并以电缆的中心线计算各圈的长度,精确到米]
答案:776m
(提示:根据题意,从最内层开始计算,第一层排了18股电缆,每股电缆长为
a1=2π(0.70+0.04);第二层也排了18股电缆,每股电缆长为
a2=2π(0.70+0.04+0.08);…;第七层同样排了18股电缆,每股电缆长为
a7=2π(0.70+0.04+6×0.08);
则每层电缆的长度构成一个等差数列,其长度总和为S= 18(a1+ a2+…+ a7)
=18π(0.74+1.22)×7=776m
15. (文)若函数f(x)=x2+(m-1)x+n+3,x∈[m,a]的图象关于直线x=-2对称,则a=__________
答案:-9(提示:由对称轴为x=-2得,-![]() =-2,∴m=5,图象关于直线x=-2对称,定义域必须也关于x=-2对称,∴
=-2,∴m=5,图象关于直线x=-2对称,定义域必须也关于x=-2对称,∴![]() =-2,∴a=-9,填-9)
=-2,∴a=-9,填-9)
15.(理)若二次函数f1(x)=a1x2+b1x+c1和f2(x)=a2x2+b2x+c2使得f1(x)+f2(x)在(-∞,4)上单调增加,在(4,+∞)上单调递减,试写出一组满足上述要求的二次函数:
f1(x)=_______;f2(x)=__________(注:填上你认为正确的一组函数即可,不必考虑所有可能的情况)
答案:不唯一(提示:两函数只要满足a1+a2<0,且-![]() =4即可。)
=4即可。)
16. (文)已知函数f(x)=3x的反函数是f -1(x),且f -1(6)=a+1,则函数y=3 ax (x∈[0,2])的值域为
_________________________
答案:[1,4](提示:f-1(x)=1og3x,∴f –1 (6)=1og36=a+1,∴a=1og32,∴y=3ax=
3 log32·x = (3log32)x=2x,∵x∈[0,2],∴值域为[1,4])
16.(理)点集C1、C2、C3、C4分别表示函数f1(x)=3x,f2(x)= 3x,f3(x)=3-x ,f4(x)=3-x的图象,给出以下四个命题:
①C1![]() C2;②C4
C2;②C4![]() C3;③C1∪C3= C4∪C2;④C1∩C3=C2∩C4
C3;③C1∪C3= C4∪C2;④C1∩C3=C2∩C4
其中正确的命题是________
答案:③④(提示:只要分别画出四个函数的图象,即可判断出③④正确)
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤
17(本小题12分)甲、乙两个篮球运动员,投篮的命中率分别为0.7与0.8,如果每人投篮两次,
(1)求甲投进2球且乙投进1球的概率;
(2)若投进1个球得2分,未投进得0分,求甲、乙两人得分相等的概率
解:(1)设甲投进二球乙投进一球的事件为A,则
P(A)=P2(2)·P′2(1)=(C![]() 0.72×0.30)·(C
0.72×0.30)·(C![]() 0.8×0.2)=0.1568
(5分)
0.8×0.2)=0.1568
(5分)
(2)设甲、乙得分相等的事件为B,则
P(B)=P2(2)·P′2(2)+P2(1)·P′2(1)+P2(0)·P′2(0)
= C![]() 0.72·C
0.72·C![]() 0.82+(C
0.82+(C![]() 0.7×0.3)·(C
0.7×0.3)·(C![]() 0.8×0.2)+C
0.8×0.2)+C![]() 0.32·C
0.32·C![]() 0.22=0.4516 (12分)
0.22=0.4516 (12分)
18(文,本小题12分)已知ΔABC中,A、B、C分别是三个内角,a、b、c分别是角A、B、C的对边,已知2![]() (sin2A-sin2C)=(a-b)sinB,ΔABC的外接圆的半径为
(sin2A-sin2C)=(a-b)sinB,ΔABC的外接圆的半径为![]() ,
,
(1)求角C
(2)求ΔABC面积S的最大值
解:(1)2![]() (sin2A-sin2C)=(a-b)sinB,
(sin2A-sin2C)=(a-b)sinB,
又2R=2![]() ,由正弦定理得:
,由正弦定理得:
2![]()
![]() =(a-b)
=(a-b)![]() ,
,
∴a2-c2=ab-b2, a2+b2-c2=ab
结合余弦定理得:
2ab cosC=ab,∴cosC=![]()
又∵0<C<π,∴C=![]() (6分)
(6分)
(2)法一:S=![]() ab sinC=
ab sinC=![]() ab sin
ab sin![]() =
=![]() 2RsinA·2RsinB
2RsinA·2RsinB
=2![]() sinA sinB= -
sinA sinB= -![]() [cos(A+B)-cos(A-B)]
[cos(A+B)-cos(A-B)]
∵A+B=![]()
∴S=![]() +
+![]() cos(A-B)
cos(A-B)
故当cos(A-B)=1,即A=B=![]() 时
时
Smax=![]() +
+![]() =3
=3![]() (12分)
(12分)
法二:S=![]() ab sinC=
ab sinC=![]() ab sin
ab sin![]() =
=![]() 2R sinA·2R sinB=2
2R sinA·2R sinB=2![]() sinA sinB
sinA sinB
=2![]() sinA sin(
sinA sin(![]() -A)=2
-A)=2![]() sinA(sin
sinA(sin![]() cosA-cos
cosA-cos![]() sinA)
sinA)
=2![]() sinA(
sinA(![]() cosA+
cosA+![]() sinA)=
sinA)= ![]() (
(![]() sinA cosA+sin2A)
sinA cosA+sin2A)
=![]() [
[![]() sin2A+
sin2A+![]() (1-cos2A)]
(1-cos2A)]
=![]() (
(![]() sin2A-
sin2A-![]() cos2A)+
cos2A)+ ![]()
=![]() sin(2A-
sin(2A-![]() )+
)+ ![]() ≤
≤![]() +
+![]() =3
=3![]()
 当2A-
当2A-![]() =
=![]() 时,即A=
时,即A=![]() 时,Smax=3
时,Smax=3![]() (12分)
(12分)
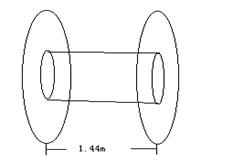
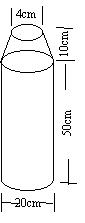
18.(理,本小题12分)2001年6月3日进行抚仙湖水下考古,潜水员身背氧气瓶潜入湖底进行考察,氧气瓶形状如图,其结构为一个圆柱和一个圆台的组合(设氧气瓶中氧气已充满,所给尺寸是氧气瓶的内径尺寸),潜水员在潜入水下a米的过程中,速度为 v 米/分,每分钟需氧量与速度平方成正比(当速度为1米/分时,每分钟需氧量0.2L);在湖底工作时,每分钟需氧量为0.4 L;返回水面时,速度也为 v 米 /分,每分钟需氧量为 0.2 L,若下潜与上浮时速度不能超过p 米 /分,试问潜水员在湖底最多能工作多少时间?(氧气瓶体积计算精确到1L,a,p为常数)
【解答】首先计算氧气瓶中氧气的体积,
V=V![]() +V
+V![]() =π×10
=π×10 ![]() ×50+π×10×
×50+π×10×![]() (4+20+100)
(4+20+100)
≈5413π≈16997cm![]() =17 L
(3分)
=17 L
(3分)
然后计算用氧时间:设潜入水下a米过程中的每分钟需氧量为Q,则Q=kv 2,
因当速度为1m/分时,每分钟需氧量0.2L,所以k=0.2,
故来回途中需氧量为a×0.2v+a×![]() v∈(0,p)
v∈(0,p)
则在湖底的工作时间为![]() [17-(0.2av+
[17-(0.2av+![]() )], (6分)
)], (6分)
∵0.2av+![]() ≥0.4a,当且仅当v=1时取等号,所以
≥0.4a,当且仅当v=1时取等号,所以
当p≥1时,![]() [17-(0.2av+
[17-(0.2av+![]() )]的最大值是42.5-a;
(8分)
)]的最大值是42.5-a;
(8分)
当p<1时,v∈(0,p),
![]() [17-(0.2av+
[17-(0.2av+![]() )]-
)]-![]() [17-(0.2ap+
[17-(0.2ap+![]() )]
)]
=![]() ,
,
∵v≤p<1,vp≤p2<1,
∴![]() [17-(0.2av+
[17-(0.2av+![]() )]-
)]-![]() [17-(0.2ap+
[17-(0.2ap+![]() )]
)]
=![]() ≤0,
≤0,
即当v=p时,在湖底的工作时间的最大值为![]() [17-(0.2ap+
[17-(0.2ap+![]() )]
)]
因此,当p≥1时,潜水员在湖底最多能工作42.5-a分钟;当p<1时,潜水员在湖底最多能工作![]() [17-(0.2ap+
[17-(0.2ap+![]() )]分钟
(12分)
)]分钟
(12分)
19(本小题12分)甲、乙两题任选一题
(甲)如图(a)所示,正三棱柱ABC-A1B1C1的底面边长为a,点M在边BC上,ΔAMC1是以点M为直角顶点的等腰直角三角形.
(1)求证点M为边BC的中点;
(2)求点C到平面AMC1的距离;
(3)求二面角M-AC1-C的大小
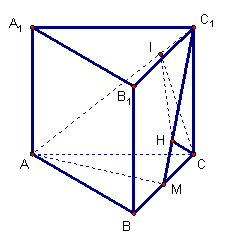
(乙)如图(b),直三棱柱ABC-A1B1C1中,底面是∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点,
(1)求直线BE与A1C所成的角;
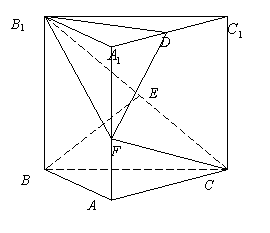 (2)在线段AA1上是否存在点F,使CF⊥平面B1DF,若存在,求出|
(2)在线段AA1上是否存在点F,使CF⊥平面B1DF,若存在,求出|![]() |;若不存在,说明理由
|;若不存在,说明理由
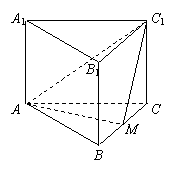 |
(a) (b)
解:(甲)(1)∵△AMC1为以点M为直角顶点的等腰直角三角形,
∴AM⊥C1M且AM=C1M
∵正三棱柱ABC-A1B1C1
∴CC1⊥底面ABC且底面ABC为正三角形
∴C1M在底面内的射影为CM,AM⊥CM
∵底面ABC为边长为a的正三角形
∴点M为BC的中点 (4分)
 (2)过点C作CH⊥MC1
(2)过点C作CH⊥MC1
由(1)知AM⊥C1M且AM⊥CM
∴AM⊥平面C1CM
∵CH在平面C1CM内,∴CH⊥AM
∴CH⊥平面C1AM
由(1)知AM=C1M=![]() a,CM=
a,CM=![]() a,且CC1⊥BC
a,且CC1⊥BC
∴CC1=![]() =
=![]() a
a
∴CH=![]() =
=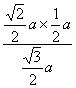 =
=![]() a
a
∴点C到平面AMC1的距离为![]() a
(8分)
a
(8分)
(3)过点C作CI⊥AC1于I,连HI
∵CH⊥平面C1AM
∴HI为CI在平面C1AM内的射影
∴HI⊥AC1,∠CIH是二面角M-AC1-C的平面角
在直角三角形ACC1中
CI=![]() =
=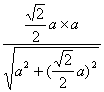 =
=![]() a
a
sin∠CIH=![]() =
=![]() =
=![]()
∴∠CIH=45°
∴二面角M-AC1-C的大小为45° (12分)
(乙)(1)∵以B为原点,建立如图所示的空间直角坐标系(图略)
∵AC=2a,∠ABC=90°
∴AB=BC=![]() a
a
∴B(0,0,0), C(0, ![]() a, 0),
A(
a, 0),
A(![]() a,0,0)
a,0,0)
A1(![]() a,0,3a), C1(0,
a,0,3a), C1(0,
![]() a,3a),
B1(0,0,3a)
a,3a),
B1(0,0,3a)
∴D(![]() a,
a, ![]() a,3a), E(0,
a,3a), E(0, ![]() a,
a,![]() a),
(3分)
a),
(3分)
∴CA1=(![]() a,-
a,- ![]() a,3a)
a,3a)
BE=(0, ![]() a,
a, ![]() a)
a)
∴|![]() |=
|=![]() a,|
a,|![]() |=
|=![]() a
a
∴![]() ·
·![]() =0-a2+
=0-a2+![]() a2=
a2=![]() a2
a2
∴cosθ=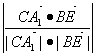 =
=![]()
故BE与A1C所成的角为arc cos![]() (6分)
(6分)
(2)假设存在点F,使CF⊥平面B1DF,不妨设AF=b,
∴F(![]() a,0,b),
a,0,b), ![]() =(
=(![]() a,-
a,- ![]() a, b),
a, b), ![]() =(
=(![]() a,0,b-3a)
a,0,b-3a)
![]() =(
=(![]() a,
a, ![]() a, 0)
(8分)
a, 0)
(8分)
∵![]() ·
·![]() =a2-a2=0,∴CF⊥B1D恒成立
(9分)
=a2-a2=0,∴CF⊥B1D恒成立
(9分)
由![]() ·
·![]() =2a2+b(b-3a)=0
=2a2+b(b-3a)=0![]() b=a或b=2a
b=a或b=2a
故当|![]() |=a或2a时,CF⊥平面B1DF
(12分)
|=a或2a时,CF⊥平面B1DF
(12分)
20(理,本小题12分)已知a、b、c为正整数(a≠1)等差数列{an}的首项为a,公差为b,等比数列{bn}的首项为b,公比为a,满足条件:a<b,且b2<a3,在数列{an}和数列{bn}中各存在一项am与bn有am+1=bn成立,又设cn=(![]() )·log2
)·log2![]()
(1)求a, b的值
(2)求数列{cn}中的最小项,并说明该项是数列{cn}中的第几项?
(3)若数列![]() 为等差数列,求常数p
为等差数列,求常数p
解:(1)由b2<a3即题意有ab<a+2b<3b(∵a<b)
b为正整数,∴1<a<3,而a为正整数,∴a=2
又am+1=bn,∴1+2+(m-1)b=b·2n-1,即b=![]() ∈Z+,
∈Z+,
只有2n-1-m+1=1方可,∴b=3 (4分)
(2)an=2+3(n-1),bn=3×2n-1,∴b2n+1=3×22n
∴cn=(n-5)×2n=2n2-10n,利用二次函数并结合n为正整数,当n=2或3时,
cn取得最小值-12 (8分)
(3)法一:设![]() =
=![]() =2n+t
=2n+t
则2n2-10n=2n2+(2p+t)n+pt
∴![]() ∴
∴![]() 或
或 ![]()
∴当p=0或p=-5时,数列![]() 为等差数列
(12分)
为等差数列
(12分)
法二:∵![]() =
=![]() ,
, ![]() =
=![]() ,
,![]() =
=![]() ,
,
又∵![]() 为等差数列
为等差数列
∴2×![]() =
=![]() +
+![]() ,即p2+5p=0
,即p2+5p=0
∴p=0或-5 (12分)
20.(文,本题12分)已知函数f(x)=x2-2xsecα+tan2α
(1)证明:方程f(x)=0有两个相异实根;
(2)当cosα=![]() (k∈N*)时,设方程f(x)=0的两根分别为xk、x’k,试求
(k∈N*)时,设方程f(x)=0的两根分别为xk、x’k,试求![]() (其中
(其中![]() 表示a1、a2、…、an的和,n∈N*,n≥2)
表示a1、a2、…、an的和,n∈N*,n≥2)
(3)在(2)下,设Ak(xk,0),Bk(xk’,0)( xk <xk’ ,Ck(secα,-1),求所有△AkBkCk(k=1,2, …,n)所围成的图形的面积Pn
解:(1)∵△=4 sec2α-4 tan2α=4>0,
∴方程有两个相异实根。 (3分)
(2)∵tan2α=k2-1,
f(x)=x2-2kx+k2-1=0,
∴![]() (7分)
(7分)
(3)∵xk =k-1, xk’=k+1
∴AkBk= xk’ - xk=2
又点Ck(k,-1)到x轴距离为1,∴S△![]() =
=![]() ·2·1=1
·2·1=1
∴Pn=n S△![]() -
-![]() (n-1)=
(n-1)=![]() (3 n+1)
(12分)
(3 n+1)
(12分)
21(本小题12分)设x、y∈R,![]() ,
, ![]() 为直角坐标平面内x,y轴正方向上的单位向量,若向量
为直角坐标平面内x,y轴正方向上的单位向量,若向量![]() =x
=x![]() +(y+
+(y+![]() )
) ![]() ,
,![]() =x
=x![]() +(y-
+(y-![]() )
) ![]() ,且|
,且|![]() |+|
|+|![]() |= 4
|= 4
(1) 求点M(x,y)的轨迹C的方程;
(2)
过点(0,1)作直线l与曲线C交于A、B两点,设![]() =
=![]() +
+![]() .是否存在这样的直线l,使得四边形OAPB是矩形?若存在,求出直线l的方程;若不存在,试说明理由
.是否存在这样的直线l,使得四边形OAPB是矩形?若存在,求出直线l的方程;若不存在,试说明理由
解:(1)法一:∵![]() =x
=x![]() +(y+
+(y+![]() )
) ![]() ,
,![]() =x
=x ![]() +(y-
+(y-![]() )
) ![]()
且|![]() |+|
|+|![]() |=4,∴点M(x,y)到两个定点F1(0,-
|=4,∴点M(x,y)到两个定点F1(0,-![]() ),
),
F2(0,![]() )的距离之和为4
)的距离之和为4
∴轨迹C为以F1、F2为焦点的椭圆,方程为![]() +x2=1
(4分)
+x2=1
(4分)
法二:由题意知
![]() +
+![]() =4
=4
移项得![]() =4-
=4-![]()
两边平方,得x2+(y+![]() )2=x2+(y-
)2=x2+(y-![]() )2-8
)2-8![]() +16
+16
整理,得2![]() =4-
=4-![]() y
y
两边平方,得4[x2+(y-![]() )2]=(4-
)2]=(4-![]() y)2
y)2
展开,整理得![]() +x2=1
(4分)
+x2=1
(4分)
(2)∵l过y轴上的点(0,1),若直线l是y轴,则A、B两点是椭圆的顶点
∵![]() =
=![]() +
+![]() =
=![]()
∴P与O重合,与四边形OAPB是矩形矛盾 (5分)
∴直线l的斜率存在,设l的方程为y=kx+1,A(x1,y1),B(x2,y2)
由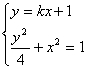 消去y得(4+k2)x2+2kx-3=0
消去y得(4+k2)x2+2kx-3=0
此时Δ=(2k)2-4(4+k2)(-3)>0恒成立
且x1+x2=
-![]() ,x1x2= -
,x1x2= -![]() (7分)
(7分)
∵![]() =
=![]() +
+![]()
∴四边形OAPB是平行四边形
若存在直线l,使得四边形OAPB是矩形
则OA⊥OB,即![]() ·
·![]() =0
=0
∵![]() =(x1,y1),
=(x1,y1), ![]() =(x2,y2)
=(x2,y2)
∴![]() ·
·![]() =x1x2+y1y2=0
(9分)
=x1x2+y1y2=0
(9分)
即(1+k2)x1x2+k(x1+x2)+1=0,也即
(1+k2)·(-![]() )+k·(-
)+k·(-![]() )+1=0
)+1=0
即k2=![]() ,解得k=±
,解得k=±![]()
∴存在直线l: y=±![]() x+1,使得四边形OAPB是矩形
(12分)
x+1,使得四边形OAPB是矩形
(12分)
22(本小题14分)已知函数f(x)=-x3+ax2+b(a,b∈R)
(1)若函数y=f(x)图像上任意不同的两点连线斜率小于1,求证:-![]() <a<
<a<![]()
(2)若x∈[0,1],函数y=f(x)上任一点切线斜率为k,讨论|k|≤1的充要条件
解:(1)设任意不同的两点P1(x1,y1),P2(x2,y2),且x1≠x2
则![]() <1
(1分)
<1
(1分)
∴![]() <1
<1
即-x12-x1x2-x22+a(x1+x2)<1
∴-x12+(a-x2)x1-x22+ax2-1<0 (3分)
∵x1∈R
∴Δ=(a-x2)2+4(-x22+ax2-1)<0
即-3x22+2ax2+a2-4<0
∴-3(x2-![]() )2+
)2+![]() +a2-4<0
+a2-4<0
∴![]() a2-4<0,∴-
a2-4<0,∴-![]() <a<
<a<![]() (6分)
(6分)
(2)当x∈[0,1]时,k=f′(x)=-3x2+2ax(7分)
由题意知:-1≤-3x2+2ax≤1,x∈[0,1]
即对于任意x∈[0,1],|f′(x)|≤1等价于|f′(0)|,|f′(1)|,
|f′(![]() )|的值满足
)|的值满足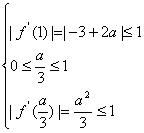
或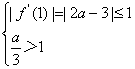 或
或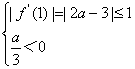 (11分)
(11分)
即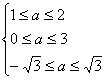 或
或 ![]() 或
或 ![]()
∴1≤a≤![]()
即|k|≤1的充要条件是1≤a≤![]() (14分)
(14分)