高考数学模拟试卷2
第I卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1、条件![]() ,条件
,条件![]() ,则
,则![]() 是
是![]() 的( )
的( )
A.充分非必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要的条件
解析: 由![]() 得
得![]() 或
或![]() , 则
, 则![]() 为
为![]() ,又由
,又由![]() 得
得![]() 为
为![]() , ∵
, ∵![]()
![]() , ∴
, ∴![]() 是
是![]() 的充分非必要条件 ,故选A
.
的充分非必要条件 ,故选A
.
2、(理)设![]() , 则此函数在区间
, 则此函数在区间 ![]() 和
和![]() 内分别为 ( )
内分别为 ( )
A.单调递增,单调递增 B.单调递增,单调递减
C.单调递减,单调递增 D.单调递减,单调递减
(文)曲线![]() 上以点(1,–1)为切点的切线方程是( )
上以点(1,–1)为切点的切线方程是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(理) 解析: ![]() ,
,
当
![]() 时,
时, ![]() , 即
, 即![]() 在
在![]() 上单调递增 ;
上单调递增 ;
当![]() 时,
时, ![]() , 即
, 即![]() 在
在![]() 上单调递减 ; 故应选B .
上单调递减 ; 故应选B .
(文)解析: 设切点坐标为(![]() ), 则切线的斜率为
), 则切线的斜率为![]() ,
,
∴所求切线方程为![]() 即
即![]() ,故选D .
,故选D .
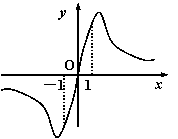 3、若函数
3、若函数![]() 的图像如图所示,则m的范围为( )
的图像如图所示,则m的范围为( )
A.(-∞,-1) B.(-1,2)
C.(1,2) D.(0,2)
解析: 由图像得![]() , 解得
, 解得 ![]() ,
,
若![]() , 则由函数的定义域得
, 则由函数的定义域得![]() , 即函数图象不连续, 与已知图象矛盾,
, 即函数图象不连续, 与已知图象矛盾,
若![]() , 则
, 则![]() 也与已知图象矛盾;
也与已知图象矛盾;
若![]() ,设
,设![]() ,则
,则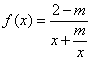 ,可得
,可得![]() 时 ,
时 , 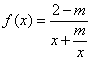 为减函数, 也与已知图象矛盾;
为减函数, 也与已知图象矛盾;
若![]() ,设
,设![]() ,则
,则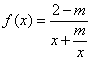 ,可得
,可得![]() 时 ,
时 , 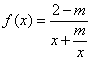 为增函数,由图象可得
为增函数,由图象可得![]() >1 ,从而得
>1 ,从而得 ![]() , 故选C .
, 故选C .
解析:由图象可知x∈R,则m>0,排除A、B;
C、D的差别在于包含1,令m=1得f(x)=![]() ,此时f(1)=1
,此时f(1)=1
与f(1)>1矛盾,故选C
4、对于直线![]() 和平面
和平面![]() ,
,![]() 的一个充分条件是( )
的一个充分条件是( )
A.![]() ∥
∥![]() B.
B.![]()
C.
![]() ∥
∥![]() ∥
∥![]() D.
D.![]() ∥
∥![]()
解析: 若![]() ∥
∥![]() 则
则![]() 又
又![]() ∴
∴![]() ,故A正确 .
,故A正确 .
注:与1题的知识点有重复考查的现象。
5、(理) 在数列![]() 中,
中,![]() ,当n≥2时,
,当n≥2时,![]() ,且已知此数列有极限,则
,且已知此数列有极限,则![]() 等于
( )
等于
( )
A.-2 B.-1 C.0 D. 1
(文)已知函数![]() ,则
,则![]() 的值为( )
的值为( )
A. 9
B. ![]() C. -9 D.
C. -9 D. ![]()
(理)解析: 由![]() , 得
, 得 ![]() , 即数列
, 即数列![]() 是以
是以![]() 为首项,公差为1的等差数列,
为首项,公差为1的等差数列, ![]() , 即
, 即![]() , ∴
, ∴![]() ,故选C .
,故选C .
解析:∵已知此数列有极限
∴设![]() =A,则有
=A,则有
![]() 故选 C
故选 C
(文)解析: ∵![]() , ∴应选B .
, ∴应选B .
6、(理)有10件产品,其中3件是次品,从中任取2件,若![]() 表示取到次品的个数,则E
表示取到次品的个数,则E![]() 等于
( )
等于
( )
A.1 B.![]() C.
C.![]() D.
D.![]()
(文) 摇奖器摇出的一组中奖号码为8,2,5,3,7,1 .对奖票上的六个数字是从0,1,2,……,9这十个数字中任意选出六个不同数字组成的. 如果对奖票上的六个数字中至少有五个与摇奖器摇出的号码相同(不计顺序)就可以得奖,则中奖的概率为( )
|
C. ![]() D.
D. ![]()
(理)解析: 列表如右图所示:
则![]() , 故应选D .
, 故应选D .
(文)解析:分两类,一类是五个数字相同,其概率为![]() , 一类是六个数字相同,其概率为
, 一类是六个数字相同,其概率为![]() ,∴中奖的概率为
,∴中奖的概率为![]() ,
,
故选D .
7、若![]() 且
且![]() ,那么
,那么![]() 的最小值是
( )
的最小值是
( )
A.2
B.![]() C.
C.![]() D.0
D.0
解析: 由![]() ,及
,及![]() 得,
得, ![]() ,
,
∴![]() ,
,
当![]() 时,
时, ![]() ,故应选B .
,故应选B .
8、一个球的内接正四棱柱的侧面积与底面积之比为4 : 1 , 体积为4![]() ,则这个球的表面积
( )
,则这个球的表面积
( )
A. 12
B. 12![]() C. 3
C. 3![]()
![]() D. 12
D. 12![]()
![]()
解析: 设正四棱柱的底面边长为![]() ,侧棱长为
,侧棱长为![]() ,由已知得
,由已知得![]() ,即
,即![]() ,∴
,∴ ![]() ,即
,即![]() .
.
∴球的直径![]() ,即
,即![]() , 从而得球的表面积
, 从而得球的表面积![]() ,故选B .
,故选B .
9、设![]() , 则对任意正整数
, 则对任意正整数![]() , 都成立的不等式是
( )
, 都成立的不等式是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
解析: ![]()
![]()
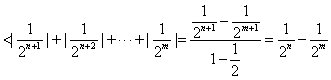
![]() . 故应选C .
. 故应选C .
10、函数![]() 与
与![]() ,(其中
,(其中![]() 且
且![]() )的图象关于 ( )
)的图象关于 ( )
A.直线![]() 对称
B.直线
对称
B.直线![]() 对称
对称
C.直线![]() 对称
D.直线
对称
D.直线![]() 对称
对称
解析: ∵函数![]() 与
与![]() 的图象关于直线
的图象关于直线![]() 对称 ,而函数
对称 ,而函数![]() 与
与![]() 的图象分别是由函数
的图象分别是由函数![]() 与
与![]() 的图象向左平移1个单位而得,
∴函数
的图象向左平移1个单位而得,
∴函数![]() 与
与![]() 的图象的对称轴可以是由直线
的图象的对称轴可以是由直线![]() 向左平移1个单位可得对称轴为
向左平移1个单位可得对称轴为![]() 故应选C .
故应选C .
11、(改编题)已知双曲线![]() 的左准线为
的左准线为![]() , 左、右焦点分别为F1、F2 , 抛物线
, 左、右焦点分别为F1、F2 , 抛物线![]() 的准线为
的准线为![]() , 焦点是F2 , 若
, 焦点是F2 , 若![]() 与
与![]() 的一个交点为P, 则
的一个交点为P, 则![]() 的值等于( )
的值等于( )
A. 40 B. 32 C. 8 D. 4
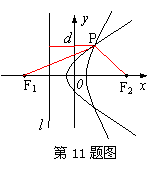 解析:如图,设
解析:如图,设![]() ,点P到直线
,点P到直线![]() 的距离
的距离
为![]() ,则由抛物线定义得
,则由抛物线定义得![]() ,
,
由点P在双曲线上,及双曲线第一定
义得![]() , 又由双曲线
, 又由双曲线
第二定义得![]() , ∴
, ∴![]() ,解之得
,解之得![]() ,故应选B .
,故应选B .
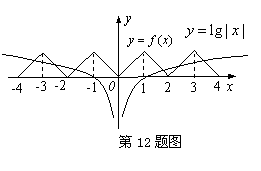 12、(改编题)若函数
12、(改编题)若函数![]() 满足
满足![]() , 且
, 且![]() 时
时![]() ,则函数
,则函数![]() 的图象与函数
的图象与函数![]() 的图象的交点个数为 ( )
的图象的交点个数为 ( )
A.16 B.18
C.20 D.无数个
解析: 由已知条件可作出函数![]()
及![]() 的图象如下图所示,由图象
的图象如下图所示,由图象
可得其交点的个数左右边有9个,共计18个 ,故应选B .
第II卷
二、填空题:本大题共4小题,每小题4分,共16分。把答案填在答题卷中相应位置上。
13.(理科做)复数![]() 的虚部为____________.
的虚部为____________.
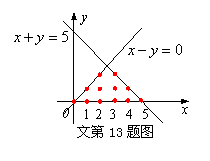 (文科做)可行域
(文科做)可行域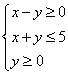 内的所有的点中,横坐标与纵坐标均为整数的整点共有______个.
内的所有的点中,横坐标与纵坐标均为整数的整点共有______个.
解析: (理)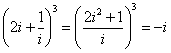 ,
,
故其虚部为-1 ;
(文)作出可行域如图所示, 可得共有12个整点.
14、函数![]() 的图象中相邻两条对称轴的距离是________;
的图象中相邻两条对称轴的距离是________;
解析: ![]() , 相邻两条对称轴间的距离就是此函数的半周期
, 相邻两条对称轴间的距离就是此函数的半周期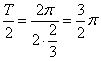 .
.
15、若![]() ,则
,则
![]() .(用数字作答)
.(用数字作答)
解析: 令![]() 得 , 得
得 , 得![]() , 令
, 令![]() , 得
, 得![]() ,
,
![]() .
.
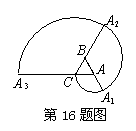 16、(竞赛题改编)如图,一条螺旋线是用以下方法画成:ΔABC是边长为1的正三角形,曲线CA1,A1A2,A2A3分别以A、B、C为圆心,
16、(竞赛题改编)如图,一条螺旋线是用以下方法画成:ΔABC是边长为1的正三角形,曲线CA1,A1A2,A2A3分别以A、B、C为圆心,
AC、BA1、CA2为半径画的弧,曲线CA1A2A3称为螺旋线
旋转一圈.然后又以A为圆心AA3为半径画弧…,这样
画到第n圈,则所得螺旋线的长度![]() .
.
(用π表示即可)
解析: ![]()
![]() .
.
三、解答题
17.(本题满分12分)
设函数f(x)= ![]() ,其中向量
,其中向量![]() =(2cosx,1),
=(2cosx,1),![]() =(cosx,
=(cosx,![]() sin2x),x∈R.
sin2x),x∈R.
(Ⅰ)若f(x)=1-![]() 且x∈[-
且x∈[-![]() ,
,![]() ],求x;
],求x;
(Ⅱ)若函数y=2sin2x的图象按向量![]() =(m,n) (m<
=(m,n) (m<![]() )平移后得到函数y=f(x)的图象,求实数m、n的值.
)平移后得到函数y=f(x)的图象,求实数m、n的值.
解:(Ⅰ)依题设,f(x)=2cos2x +![]() sin2x=1+2sin(2x
+
sin2x=1+2sin(2x
+![]() ).…………2分
).…………2分
由1+2sin(2x +![]() )=1-
)=1-![]() ,得sin(2x +
,得sin(2x +![]() )=-
)=-![]() .
.
∵-![]() ≤x ≤
≤x ≤![]() ,∴-
,∴-![]() ≤2x+
≤2x+![]() ≤
≤![]() ,∴2x+
,∴2x+![]() =-
=-![]() ,
,
即x =-![]() .……………………8分
.……………………8分
(Ⅱ)函数y=2sin2x的图象按向量![]() =(m,n)平移后得到函数
=(m,n)平移后得到函数
y=2sin2(x-m)+n的图象,即函数y=f(x)的图象.
由(Ⅰ)得 f(x)=2sin2(x+![]() )+1. ∵m<
)+1. ∵m<![]() ,∴m=-
,∴m=-![]() ,n=1.…12分
,n=1.…12分
注:本题在知识的交汇点命题的考查思路好,有一定的创新。
18.(本小题满分12分)
已知函数![]() .
.
(1)若![]() 在
在![]() [1,+∞
[1,+∞![]() 上是增函数,求实数a的取值范围;
上是增函数,求实数a的取值范围;
(2)若x=3是![]() 的极值点,求
的极值点,求![]() 在
在![]() [1,a]上的最小值和最大值.
[1,a]上的最小值和最大值.
解析:(1)![]() .
.
∵ x≥1. ∴ ![]() ,------------------------------------------------------3分
,------------------------------------------------------3分
![]() (当x=1时,取最小值).
(当x=1时,取最小值).
∴ a<3(a=3时也符合题意). ∴ a≤3.------------------------------------6分
(2)![]() ,即27-6a+3=0, ∴ a=5,
,即27-6a+3=0, ∴ a=5,![]() .
.
令![]() 得
得 ![]() ,或
,或 ![]() (舍去) --------------------------8分
(舍去) --------------------------8分
当![]() 时,
时,![]() ; 当
; 当![]() 时,
时,![]()
即当![]() 时,
时,![]() 有极小值
有极小值![]() .又
.又![]() ---------10分
---------10分
∴ f(x)在![]() ,
,![]() 上的最小值是
上的最小值是![]() ,最大值是
,最大值是![]() . ----------12分
. ----------12分
(19)(本小题满分12分)
下表为某班英语及数学成绩的分布.学生共有50人,成绩分1~5五个档次.例如表中所示英语成绩为4分、数学成绩为2分的学生为5人.将全班学生的姓名卡片混在一起,任取一枚,该卡片同学的英语成绩为![]() ,数学成绩为
,数学成绩为![]() 。设
。设![]() 为随机变量(注:没有相同姓名的学生).
为随机变量(注:没有相同姓名的学生).
(1)![]() 的概率为多少?
的概率为多少?![]() 的概率为多少?
的概率为多少?
(2) (理) ![]() 等于多少?若
等于多少?若![]() 的期望为
的期望为![]() ,试确定
,试确定![]() ,
,![]() 的值 .
的值 .
|
| 数学 | |||||
| 5 | 4 | 3 | 2 | 1 | ||
| 英语 | 5 | 1 | 3 | 1 | 0 | 1 |
| 4 | 1 | 0 | 7 | 5 | 1 | |
| 3 | 2 | 1 | 0 | 9 | 3 | |
| 2 | 1 |
| 6 | 0 |
| |
| 1 | 0 | 0 | 1 | 1 | 3 | |
(文) ![]() 等于多少?若
等于多少?若![]() 的概率为
的概率为![]() ,试确定
,试确定![]() ,
,![]() 的值 .
的值 .
解:(1)![]() ;--------6分
;--------6分
(2)(理)![]()
![]() ①;---------9分
①;---------9分
又![]()
![]() ②; - --------11分
②; - --------11分
结合①②可得![]() ,
,![]() .
---------12分
.
---------12分
(文) ![]()
![]() ①;---------9分
①;---------9分
又![]() ②; - --------11分
②; - --------11分
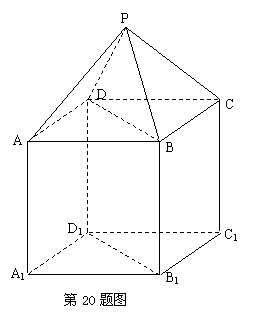 结合①②可得
结合①②可得![]() ,
,![]() .
- --------12分
.
- --------12分
20. (本小题满分12分)
如图,P—ABCD是正四棱锥,![]()
是正方体,其中![]() .
.
(1)求证:![]() ;
;
(2)求平面PAD与平面![]() 所
所
成的锐二面角![]() 的大小;
的大小;
(3)求![]() 到平面PAD的距离.
到平面PAD的距离.
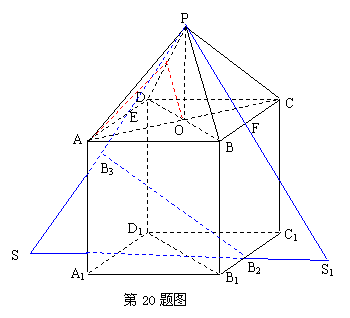
解法一: (1) 连结AC , 交BD于点O , 连结PO ,
则PO⊥面ABCD , 又∵AC⊥BD , ∴![]() ,
,
∵BD∥B1D1 , ∴![]() . ------4分
. ------4分
(2) ∵AO⊥BD , AO⊥PO ,
∴AO⊥面PBD ,
过点O作OM⊥BD于点M,连结AM ,
则AM⊥BD ,
∴∠AMO 就是二面角A-PD-O的平面角, ------6分
又∵![]() , ∴
, ∴![]() ,
,
![]() , ∴
, ∴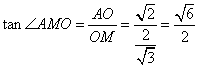 ,
,
即二面角的大小为![]() . ------8分
. ------8分
(3) 分别取AD , BC中点E , F ,作平面PEF , 交底面与两点S , S1 , 交B1C1于点B2 , 过点B2作B2B3⊥PS于点B3 , 则 B2B3⊥面PAD , 又 B1C1∥AD ,
∴B2B3的长就是点B1到平面PAD 的距离 . ------10分
∵PO=AA1=2 ,
∴![]() ,
, ![]() ,
, ![]()
∴![]() .
------12分
.
------12分
解法二: 以![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴建立空间直角坐标系
轴建立空间直角坐标系
(1)设E是BD的中点,![]() P—ABCD是正四棱锥,
P—ABCD是正四棱锥,![]()
又![]() ,
, ![]()
![]()
![]()
![]() 即
即![]() ------4分
------4分
(2)设平面PAD的法向量是![]() ,
, ![]()
![]() 取
取![]() 得
得![]() ,
,
又平面![]() 的法向量是
的法向量是![]()
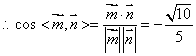
![]() ------8分
------8分
(3)![]()
![]() 到平面PAD的距离
到平面PAD的距离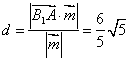 -----12分
-----12分
21. (本小题满分12分)
已知△OPQ的面积为S,且![]() ;
;
(1)若![]() ,求向量
,求向量![]() 的夹角
的夹角![]() 的取值范围;
的取值范围;
(2)设![]() 以O为中心,P为焦点的椭圆经过点Q,当
以O为中心,P为焦点的椭圆经过点Q,当![]() 上变动时,求
上变动时,求![]() 的最小值,并求出此时的椭圆方程.
的最小值,并求出此时的椭圆方程.
解:(1)∵![]() 夹角为
夹角为![]() ,∴
,∴![]() 与
与![]() 夹解为
夹解为![]() ,
,
∴![]()
又![]() ∴
∴![]()
![]() ∴
∴![]() ∴
∴![]() -----------------------------4分
-----------------------------4分
(2)以O为原点,![]() 所在直线为x轴建立直角坐标系,
----------------5分
所在直线为x轴建立直角坐标系,
----------------5分
∴![]()
∴![]() ∴
∴![]() ,
-----------6分
,
-----------6分
由![]() ∴
∴![]()
∴![]() ∴
∴![]() -------------8分
-------------8分
令![]() 上是增函数,
上是增函数,
∴![]() 上为增函数,
上为增函数,
∴当m=2时,![]() ----------9分
----------9分
此时P(2,0),椭圆另一焦点为P′(-2,0),则椭圆长轴长
![]() ,
,
![]() 故椭圆方程为
故椭圆方程为![]() -------------------------12分
-------------------------12分
22、(本题满分14分) (下而还有一备用题)
已知数集序列{1}, {3, 5}, {7, 9,11}, {13, 15, 17, 19},……,其中第n个集合有n个元素,每一个集合都由连续正奇数组成,并且每一个集合中的最大数与后一个集合最小数是连续奇数,
(Ⅰ) 求第n个集合中最小数an的表达式;
(Ⅱ)求第n个集合中各数之和Sn的表达式;
(Ⅲ)令f(n)=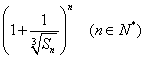 ,求证:2≤
,求证:2≤![]() .
.
解析: (Ⅰ) 设第n个集合中最小数an , 则第![]() 个集合中最小数
个集合中最小数![]() ,
,
又第![]() 个集合中共有
个集合中共有![]() 个数, 且依次增加2 ,
个数, 且依次增加2 ,
∴![]() ,即
,即 ![]() , ------2分
, ------2分
∴![]()
![]()
![]() ,
,
相加得![]() ,即得
,即得![]() .
.
又![]() , ∴
, ∴![]() .
------4分
.
------4分
(Ⅱ)由(Ⅰ)得![]() ,
,
从而得![]() .
- -----8分
.
- -----8分
(Ⅲ)由(Ⅱ)得![]() , ∴
, ∴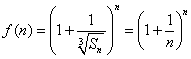
![]() ,
,
∵![]()
≥![]() , -
-----10分
, -
-----10分
又当![]() ≥2 时,
≥2 时, ![]()
≤![]() .
- -----12分
.
- -----12分
∴![]()
≤![]()
![]() .
.
∴ 2≤![]() .
- -----14分
.
- -----14分
22题 备用题(理)现有一组互不相等且从小到大排列的数据:![]() ,其中
,其中![]() .为提取反映数据间差异程度的某个指标,今对其进行如下加工:记
.为提取反映数据间差异程度的某个指标,今对其进行如下加工:记![]() ,
,![]() ,作函数
,作函数![]() ,使其图象为逐点依次连接点
,使其图象为逐点依次连接点![]() 的折线(
的折线(![]() ).
).
(Ⅰ)求![]() 和
和![]() ;
;
(Ⅱ)设![]() 的斜率为
的斜率为![]() (
(![]() ),判断
),判断![]() 的大小关系;(Ⅲ)证明:当
的大小关系;(Ⅲ)证明:当![]() 时,
时,![]() ;
;
(Ⅳ)求由函数![]() 与
与![]() 的图象所围成图形的面积(用
的图象所围成图形的面积(用![]() 表示).
表示).
(文)已知![]() 是等比数列,
是等比数列,![]() ;
;![]() 是等差数列,
是等差数列,![]() ,且满足
,且满足![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)求数列![]() 的前
的前![]() 项和
项和![]() 的公式;
的公式;
(Ⅲ)设![]() ,
,![]() ,其中
,其中![]() .试比较
.试比较![]() 与
与![]() 的大小,并证明你的结论.
的大小,并证明你的结论.
(理)解析:简解如下:(Ⅰ)![]() 和
和![]() ;
;
(Ⅱ)![]() ,
,![]() ,因为
,因为![]() ,所以
,所以![]() ;
;
(Ⅲ)首先证明![]() ,即
,即![]() ,以
,以![]() 为例,
为例,![]()
![]()
同理可证![]() 时,
时,![]() 都成立;根据
都成立;根据![]() 时,
时,![]() 都成立再证明
都成立再证明![]() 时
时![]() 也成立.事实上,
也成立.事实上,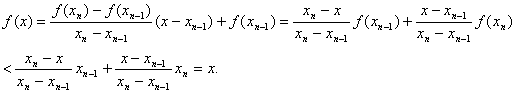 ,
,
函数![]() 的图象为逐点依次连接点
的图象为逐点依次连接点![]() 的折线(
的折线(![]() ),由上面的证明,结合
),由上面的证明,结合![]() 已经证明当
已经证明当![]() 时,
时,![]() ;
;
(Ⅳ)设![]() 为
为![]() 上折线
上折线![]() 与
与![]() 轴及直线
轴及直线![]() 所围成的图形的面积,则
所围成的图形的面积,则![]()
![]()
![]()
![]()
![]() 与
与![]() 的图象所围成图形的面积为
的图象所围成图形的面积为![]()
![]() .
.
(文)解:(Ⅰ)![]() 的公比为
的公比为![]() ,则
,则![]() ,若
,若![]() 则
则![]() 与题意不符,故
与题意不符,故![]() ,
,![]() .设
.设![]() 的公差为
的公差为![]() ,由
,由![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
(Ⅱ)![]() .
.
(Ⅲ)![]() ,
,![]() ,作差得
,作差得![]() ,对于
,对于![]() ,当
,当![]() 时
时![]() ,即
,即![]() ;当
;当![]() 时
时![]() ;当
;当![]() 时
时![]() .
.
高考要求摘录
对数学基础知识的考查:既要全面又要突出重点,对于支撑学科知识体系的重点内容,要占有较大的比例,构成数学试卷的主体,注重学科的内存联系和知识的综合性,不刻意追求知识的覆盖面,从学科的整体高度和思维价值的高度考虑问题,在知识网络交汇点设计试题,使对数学知识的考查达到必要的深度。
对数学思想和方法的考查:是对数学知识在更高层次上的抽象和概括的考查,考查时必须要与数学知识相结合,通过数学知识的考查,反映考生对数学思想和方法的理解,要从学科整体意义和思想价值立意,注重通用性通法、淡化特殊技巧,有效地检测考生对中学数学知识中所蕴含的数学思想和方法的掌握程度。
对数学能力的考查:强调“以能力立意”,就是以数学知识为载体,从问题入手,把握学科的整体意义,用统一的数学观点组织材料,侧重体现对知识的理解和应用,尤其是综合和灵活的应用,以此来检测考生将知识迁移到不同环境中去的能力,从而检测出考生个体理性思维的广度和深度。以及进一步学习的能力。
本试卷我因时间关系未仔细研究,大体上看了一下,谈点看法:
高考命题原则中对基础知识考查的要求是:既要全面又要突出重点,对于支撑学科知识体系的重点内容,要占有较大的比例,构成数学试卷的主体,注重学科的内存联系和知识的综合性,不刻意追求知识的覆盖面,从学科的整体高度和思维价值的高度考虑问题,在知识网络交汇点设计试题,使对数学知识的考查达到必要的深度。重点知识重点考查,对新增内容要有一定的考查,但不过分突出考查新增内容。
作点分析:全试卷对各章考查的大概情况如下:
1.导数内容(文、理科)考查了大约17分;
2.概率内容(包括排列组合二项式定理)(文、理科)考查了约21分;
3.向量内容(文、理科)考查了约12分;
4.函数内容(文科25分,理科20分,无大题)
5.数列与极限(文科18分,理科23分)
6.不等式(文科5分,理科5分)
7.三角函数(文科10分,理科10分)
8.立体几何(文科22分,理科22分)
9.解析几何(文科15分,理科11分)
10.集合与简易逻辑(文理5分)
试卷从知识的覆盖面来看还是作得很好,题目基本上没有陈旧的,注重了在知识的交汇点命题。在重点内容和新增内容考查的比例的上,数学方法、能力的考查方式可以再斟酌。