高考数学模拟试卷
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。供150分。考试用时120分钟。
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.集合![]() 与
与![]() 之间的关系是
之间的关系是
(![]() )
)![]()
![]()
![]() (
(![]() )
)![]()
![]()
![]() (
(![]() )
)![]()
![]() (
(![]() )
)![]() ∩
∩![]()
![]()
2.一个正四棱锥的中截面面积是![]() ,则它的底面边长是
(
,则它的底面边长是
(![]() )
)![]() (
(![]() )
)![]() (
(![]() )
)![]() (
(![]() )
)![]()
3.函数![]() ,
,![]() 的值域是
的值域是
(![]() )
)![]() (
(![]() )
)![]() (
(![]() )
)![]() (
(![]() )
)![]()
4.已知直线![]() 、
、![]() 和平面
和平面![]() ,则
,则![]() ∥
∥![]() 的一个必要但不充分条件是
的一个必要但不充分条件是
(![]() )
)![]() ∥
∥![]() 且
且![]() ∥
∥![]() (
(![]() )
)![]()
![]() 且
且![]()
![]()
(![]() )
)![]() 、
、![]() 与
与![]() 成等角 (
成等角 (![]() )
)![]() ∥
∥![]() 且
且![]()
![]()
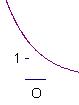
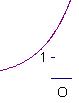
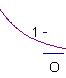
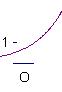
5.已知![]() 且
且![]() ,
,![]() ,则
,则![]() 的图象是
的图象是
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(![]() ) (
) (![]() ) (
) (![]() )
(
)
(![]() )
)
6.已知函数![]() ,则它的单调区间是
,则它的单调区间是
(![]() )
)![]() (
(![]() )
)![]() (
(![]() )
)![]() (
(![]() )
)![]() 及
及![]()
7.若向量![]() 、
、![]() 的坐标满足
的坐标满足![]()
![]() ,
,![]()
![]() ,则
,则![]() ·
·![]() 等于
等于
(![]() )
)![]() (
(![]() )
)![]() (
(![]() )
)![]() (
(![]() )
)![]()
8.圆![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,圆心为
两点,圆心为![]() ,若
,若![]()
![]() ,则实数
,则实数![]() 等于
等于
(![]() )
)![]() (
(![]() )
)![]() (
(![]() )
)![]() (
(![]() )
)![]()
9.一个项数是偶数的等比数列,它的偶数项的和是奇数项和的![]() 倍,又它的首项为
倍,又它的首项为![]() ,且中间两项的和为24,则此等比数列的项数为
,且中间两项的和为24,则此等比数列的项数为
(![]() )
)![]() (
(![]() )
)![]() (
(![]() )
)![]() (
(![]() )
)![]()
10.直线![]() 、
、![]() 的倾斜角的取值范围是
的倾斜角的取值范围是
(![]() )
)![]() (
(![]() )
)![]() ∪
∪![]() (
(![]() )
)![]() (
(![]() )
)![]() ∪
∪![]()
11.设函数![]() ,则
,则![]() 的值等于
的值等于
(![]() )
)![]() (
(![]() )
)![]() (
(![]() )
)![]() (
(![]() )
)![]()
12.由等式![]()
![]() 定义
定义![]() ,则
,则![]() 等于
等于
(![]() )
)![]() (
(![]() )
)![]() (
(![]() )
)![]() (
(![]() )
)![]()
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
13.已知![]() ,
,![]() ,则
,则![]() 的值是
.
的值是
.
14.已知抛物线![]() 的准线方程是
的准线方程是![]() ,那么抛物线的焦点坐标是 .
,那么抛物线的焦点坐标是 .
15.停车场划出一排![]() 个停车位置,今有3辆不同型号的车需要停放,若要求剩余的
个停车位置,今有3辆不同型号的车需要停放,若要求剩余的![]() 个空车位连在一起,则不同的停车方法数为
.
个空车位连在一起,则不同的停车方法数为
.
16.设函数![]() ·
·![]() ,给出下列命题:
,给出下列命题:
①![]() ,
,![]() 时,
时,![]() 只有一个实数根;
只有一个实数根;
②![]() 时,
时,![]() 是奇函数;
是奇函数;
③![]() 的图象关于点
的图象关于点![]() 对称;
对称;
④方程![]() 至多有2个实数根.
至多有2个实数根.
上述命题中的所有正确命题的序号是 .
三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)
已知![]() ,解关于
,解关于![]() 的不等式
的不等式![]() .
.
18.已知函数![]() ,且
,且![]() 、
、![]() 、
、![]() 成等差数列.
成等差数列.
(1)求实数![]() 的值;
的值;
(2)若![]() 、
、![]() 、
、![]() 是两两不相等的正数,且
是两两不相等的正数,且![]() 、
、![]() 、
、![]() 成等比数列,试判断
成等比数列,试判断![]() 与
与![]() 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
19.(本小题满分12分)
在某次考试中,甲、乙、丙三人合格(互不影响)的概率分别是![]() ,
,![]() ,
,![]() ,
,
 考试结束后,最容易出现几人合格的情况?
考试结束后,最容易出现几人合格的情况?
20.(本小题满分12分)
如图,在多面体![]() 中,
中,![]() 面
面![]() ,
,![]() ∥
∥![]() ,且
,且![]()
![]() ,
,![]() ,
,![]() 为
为![]() 中点.
中点.
(1)求证:![]() 面
面![]() ;
;
(2)求多面体![]() 的体积;
的体积;
(3)求面![]() 与面
与面![]() 所成的二面角的余弦值.
所成的二面角的余弦值.
21.(本小题满分12分)
某村2002年底全村共有1000人,全年工农业总产值为840万元.
(1)若从2003年起该村每年的工农业总产值较上年增加14 万元,每年人口较上年净增数相同,要使该村人均产值年年都增长,那么该村每年人口的净增不超过多少人?
(2)若从2003年起该村每年工农业总产值较上年增长![]() ,每年人口较上年净增10人,则到2012年该村能否实现年人均产值较2002年翻一番(增加一倍)的经济发展目标?
,每年人口较上年净增10人,则到2012年该村能否实现年人均产值较2002年翻一番(增加一倍)的经济发展目标?
22.(本小题满分14分)
已知动点![]() 与双曲线
与双曲线![]() 的两个焦点
的两个焦点![]() 、
、![]() 的距离之和为定值,且
的距离之和为定值,且![]()
![]() 的最小值为
的最小值为![]() .
.
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)若已知![]() ,
,![]() 、
、![]() 在动点
在动点![]() 的轨迹上且
的轨迹上且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
高三数学试卷参考答案
一、选择题:CBDCBD ABCBDD (每小题5分)
二、填空题:13.![]() 14.
14.![]() 15.
15.![]() 16.①②③
16.①②③
三、解答题:
17.解:不等式![]() 可化为
可化为![]() .………………………………………2分
.………………………………………2分
∵![]() ,∴
,∴![]() ,故原不等式可化为
,故原不等式可化为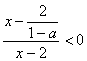 ,………………………… 4分
,………………………… 4分
故当![]() 时,原不等式的解集为
时,原不等式的解集为![]() ;………………………… 7分
;………………………… 7分
当![]() 时,原不等式的解集为
时,原不等式的解集为![]() ;…………………………………………………… 9分
;…………………………………………………… 9分
故当![]() 时,原不等式的解集为
时,原不等式的解集为![]() .………………………………12分
.………………………………12分
18.解: 解:⑴由![]() 、
、![]() 、
、![]() 成等差数列,
成等差数列,
可得![]()
![]()
![]() ,…………………………………………2分
,…………………………………………2分
即![]() 且
且![]() ,解得
,解得![]() .………………………………………4分
.………………………………………4分
⑵由![]() ,可得
,可得![]() ,
,
![]() ,…………………7分
,…………………7分
∵![]() 、
、![]() 、
、![]() 成等比数列,∴
成等比数列,∴![]() ,…………………………………………………8分
,…………………………………………………8分
又![]() 、
、![]() 、
、![]() 是两两不相等的正数,
是两两不相等的正数,
故![]() ,
,
∴![]()
![]() ,即
,即![]() .………………12分
.………………12分
19. 按以下四种情况计算概率,概率最大的就是最容易出现的情况.
⑴三人都合格的概率![]() ………………………………………………2分
………………………………………………2分
⑵三人都不合格的概率为![]() ……………………… 4分
……………………… 4分
⑶恰有两人合格的概率
![]() …………………………7分
…………………………7分
⑷恰有一人合格的概率![]() ………………………………… 10分
………………………………… 10分
由此可知,最容易出现恰有1人合格的情况……………………………………………12分
20. 解:(1)取![]() 中点
中点![]() ,连
,连![]() ,
,![]() .
.
∵![]() 面
面![]() ,
,![]() ∥
∥![]() ,∴
,∴![]() 面
面![]() ,
,
又![]() 面
面![]() ,∴
,∴![]() ,又
,又![]() ,
,![]() 是
是![]() 中点,
中点,
∴![]() ,∴
,∴![]()
![]() 平面
平面![]() ,∵
,∵![]() 是
是![]() 的中点且
的中点且![]() ,
,
∴![]() ∥
∥![]() 且
且![]() ,∴
,∴![]() ∥
∥![]() ,
,
又![]() ,∴
,∴![]() ,故四边形
,故四边形![]() 是平行四边形,从而
是平行四边形,从而![]() ∥
∥![]() ,
,
∴![]() 面
面![]() .…………………………………………………………………………4分
.…………………………………………………………………………4分
(2)设![]() 中点为
中点为![]() ,则由
,则由![]() 可得
可得![]() 且
且![]() ,
,
又∵![]() ∥
∥![]() ,∴
,∴![]() 与
与![]() 共面,又
共面,又![]() 面
面![]() ,故平面
,故平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,即
,即![]() 为四棱锥
为四棱锥![]() 的高.
的高.
故![]() ·
·![]() .……………………… 8分
.……………………… 8分
(3)过![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,由三垂线定理的逆定理得
,由三垂线定理的逆定理得![]() ,
,
 ∴
∴![]() 为二面角
为二面角![]() 的平面角.
的平面角.
易知![]() ,
,![]() ,
,![]() ,
,
由![]() ,
,
可得![]() ,在
,在![]() 中,
中, ![]() ,故
,故![]() ,
,
∴面![]() 与面
与面![]() 所成的二面角的余弦值为
所成的二面角的余弦值为![]() . ………………………………12分
. ………………………………12分
21.解:(1)设从2002年起的第![]() 年(2002年为第一年),该村的人均产值为
年(2002年为第一年),该村的人均产值为![]() ,
,
每年人口较上年净增数为![]() ,则
,则![]() ,……………………… 3分
,……………………… 3分
则![]() , …………………………………5分
, …………………………………5分
当且仅当![]() ,即
,即![]() 时,
时,![]() 随着
随着![]() 的增大而增大,
的增大而增大,
故要使该村人均产值年年都增长,那么该村每年人口的净增不超过16人.…………7分
(另法:由![]() 恒成立求解)
恒成立求解)
(2)由2002年该村的人均产值为![]() 万元;
万元;
2012年该村的人均产值为![]() 万元,……………………………………… 9分
万元,……………………………………… 9分
从而![]()
![]() ,
,
故到2012年该村能够实现年人均产值较2002年翻一番的经济发展目标.………… 12分
22.解:(1)由题意![]() ,设
,设![]() (
(![]() ),由余弦定理
),由余弦定理
得![]() .……………… 4分
.……………… 4分
又![]() ·
·![]() ,
,
当且仅当![]() 时,
时,![]() ·
·![]() 取最大值,
取最大值,
此时![]() 取最小值
取最小值![]() ,令
,令![]() ,解得
,解得
![]() ,
,![]() ,∴
,∴![]() ,故所求
,故所求![]() 的轨迹方程为
的轨迹方程为![]() .………… 7分
.………… 7分
(2)设![]() ,
,![]() ,则由
,则由![]() ,可得
,可得
![]() ,故
,故![]() ,………………………………… 9分
,………………………………… 9分
∵![]() 、
、![]() 在动点
在动点![]() 的轨迹上,故
的轨迹上,故![]() 且
且![]() ,
,
消去![]() 可得
可得![]() ,解得
,解得![]() ,…………………… 12分
,…………………… 12分
又![]() ,∴
,∴![]() ,解得
,解得![]() ,
,
故实数![]() 的取值范围是
的取值范围是![]() .………………………………………………………… 14分
.………………………………………………………… 14分
(其他解法及评分标准略)