高考数学模拟试题
一、选择题（本大题共12小题，每小题5分，共60分）
1.设集合M={x－1≤x＜2＝,N={xx≤a}.若M∩N≠
,则a的取值范围是（C）
A.（－∞,2） B.(－1,+∞) C.
D.［－1,1］
2、已知函数
为奇函数，则
的一个取值为
A.0 B. -π/4 C. π/2 D. π
3、设等差数列{an}的前n项和为Sn，若
，则当Sn时取得最大值时，
n的值为 （ ）
A.5 B．6 C.7 D.8
4.在5张卡片上分别写着数字1、2、3、4、5，然后把它们混合，再任意排成一行，则得到的数能被5或2整除的概率是（B）
A.0.8 B.0.6 C.0.4 D.0.2
5.若loga(a2+1)＜loga2a＜0,则a的取值范围是（C）
A.0＜a＜1
B.0＜a＜
C.＜a＜1
D.a＞0且a≠1
6.已知f(x)=ax3+3x2+2,若
,则a的值等于（C）
A.
B. 
C.
D.
7.把函数y=cosx的图象上的所有点的横坐标缩小到原来的一半，纵坐标扩大到原来的两倍，然后把图象向左平移
个单位，则所得图形表示的函数的解析式为（B）
A.y=2sin2x B.y=－2sin2x
C.y=2cos(x+)
D.y=2cos(
)
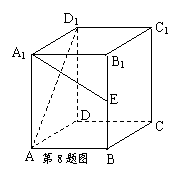8、如图，已知正四棱柱ABCD—A1B1C1D1，底面
边长为1,侧棱长为2,E为BB1的中点，则异面直线
AD1与A1E所成角的余弦值是
（A）
（B）
（C）
（D）
翰林汇
9. 如果a·b=a·c且a≠0,那么 （D）
A.b=c B.b=λc
C.b⊥c D.b、c在a方向上的投影相等
10、双曲线
的离心率为2,则
的值为
A.3 B.1/3 C.3或-1/3 D. 3或1/3
11. 二次函数f(x)的二次项系数为正，且对任意实数x，恒有f(2+x)=f(2－x),若f(1－2x2)＜f(1+2x－x2)，则x的取值范围是（C）
A.x＞2 B.x＜－2或0＜x＜2
C.－2＜x＜0 D.无法确定
12、如果直线y=kx+1与圆x2+y2+kx+my-4=0交于M、N两点，且M、N关于直线x+y=0对称，则不等式组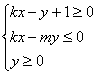
表示的平面区域的面积是
A.1/4 B.1/2 C.1 D.2
二、填空题（本大题共4小题，每小题4分，共16分）
13、定义符号函数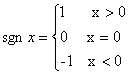
，则不等式：x+2>(2x-1)sgnx的解集是
14、以椭圆
的焦点为焦点，离心率
的双曲线的方程是
。
15.设α、β表示平面，l表示不在α内也不在β内的直线，存在下列三个事实①l⊥α,②l∥β,③α⊥β，若以其中两个作为条件，另一个作为结论，可构成三个命题，其中真命题是________.（要求写出所有真命题）
16、若数列{an}（n∈N＋）是等差数列，则有数列
也为等差数列，类比上述性质，相应地：若数列{cn}是等比数列，且cn>0（n∈N＋）,则有dn=
（n∈N＋）也是等比数列。
三、解答题（本大题共6小题，共74分）
17、甲、乙、丙三人独立参加概率分别为
，求
（1）甲、乙合格且丙不合格的概率。
（2）三人中至少有一人合格的概率。
18、已知向量
，且
，（1）求
及
；（2）求函数f(x)= -的最小值。
| A1 B1
C1 A B C |
19、如图，在三棱柱ABC-A1B1C1中,四边形A1ABB1是菱形，
且A1C⊥AB1,AB⊥BC,CB=3,AB=4,∠A1AB=60°。
（1）求证：平面CA1B⊥平面A1ABB1；
（2）求直线A1C与平面BCC1B1所成的角的正切值；
（3）求点C1到平面A1CB的距离；
20、已知抛物线y2=2px(p>0)，A、B是抛物线上不重合的任意两点，F是抛物线的焦点，且
，
，O为坐标原点。
（1）若
，求点M的坐标；
（2）求动点M的轨迹方程。
21、有一块边长为4的正方形钢板，现对其进行切割、焊接成一个长方形无盖容器（损耗不计）。有人应用数学知识作了如下设计：在钢板的四个角各切去一个小正方形，剩余部分围成一个长方体，该长方体的高为小正方形的边长。
（1）请你求出这种切割、焊接而成的长方体的最大容积V1；
（2）由于上述设计存在缺陷（材料有所浪费），请你重新设计切焊方法，使材料浪费减少，而且所得长方体的容积V2> V1；
22、设函数
，已知不论α、β为何实数，恒有
，对于正数数列
，其前n项和
（1）求b的值；（2）求数列的通项公式。
（3）问是否存在等必数列
，使得
对于一切正整数n都成立？并证明你的结论。
参考答案
一、选择题：
1.本题考查集合运算及数形结合思想。
利用数轴易求得范围为
，选C
2.本题考查三角函数的有关性质及辅助角公式的应用。
易求
，由f(0)=0,得：＝-π/4 ，选B
3. 本题考查数列的有关知识及利用函数思想解决数列的有关问题。
由，可得
，又
，而
，故此函数的对称轴为
，即时，
最大。选B
4. 本题考查排列组合及概率的相关知识。
,选B。
5、本题考查对数函数的有关知识及应用。
易知
，则由题意得：
，即：
，选C。
6、本题考查导数的有关知识的应用。
，∴
，再由
.选C。
7、本题考查三角函数的图像变换。
以上变换分别可得：
，选B
8、本题考查两异面直线所成角的求法。选A。
9、本题考查向量的有关知识及应用，选D。
10、本题考查分类讨论的知识及离心率的求法
当
时，
，求得：
当
时，
，求得：
，选D。
11、本题考查二次函数的对称性、单调性等知识的综合应用。
由题意易知函数关于直线
对称，且在区间
上为减函数。又易知：
，且f(1－2x2)＜f(1+2x－x2)，
∴
，解之得：
，选C。
12、本题考查直线与圆的有关知识及线性规划知识的综合应用。
由M、N关于直线x+y=0对称，知道kMN=1，且圆心
在直线x+y=0上，
∴m= -1,再画出不等式组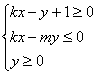的区域即可以求出其面积为1/4。选D
二、填空题：
13、解：本题考查学生的阅读理解能力及解不等式的知识。
原不等式等价于
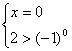或
或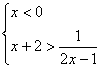
解之得：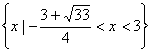
14、本题考查椭圆及双曲线的有关知识及应用。
解：易求
又
∴
，另易知焦点在y轴上，故所求的双曲线的方程为
。
15、本题考查直线与平面的位置关系的判断。可得：
。
16、解：本题考查学生类比的思想方法及研究性学习能力。
dn=
三、解答题：
17、解：（1）用A、B、C分别表示甲、乙、丙入学考试合格的事件，由题意知，事件A、B、C相互独立，则甲、乙合格且丙不合格的概率为：
（2）∵A、B、C相互独立，∴
也相互独立。
∴P=
18、解：（1）
∵
∴
又∵
, ∴
（2）
又∵, ∴
| A1 B1
C1
A B C |
O D∴当且仅当
时，f(x)取得最小值
19、本题即考查此类知识点及分析问题、解决问题的能力。
解答：（1）由A1ABB1是菱形可知：A1B⊥AB1
又A1C⊥AB1，A1B∩A1C＝A1,∴AB1⊥面CA1B
而AB1
平面A1ABB1，∴平面CA1B⊥平面A1ABB1；
（2）由（1）知：AB1⊥面CA1B ∴AB1⊥BC,
又∵AB⊥BC ∴BC⊥面A1ABB1，而BC平面C1CBB1
∴平面C1CBB1⊥面A1ABB1
作A1D⊥B1B,则A1D⊥平面C1CBB1
∴∠A1CD即位为A1C与平面BCC1B1所成的角
在矩形C1CBB1中，可求得DC=
，在正三角形A1B1B中，可求得：A1D=
∴
。
（3）∵B1C1∥BC ∴B1C1∥平面A1BC
∴C1到平面A1BC的距离即为B1到平面A1BC的距离
由（1）知：B1 O即为所求距离。
又∵B1 O＝2
∴C1到平面A1BC的距离为2。
20、解：本题考查向量知识与解析几何知识的综合应用。
设A、B的坐标分别为（x1,y1）、（x2,y2）,则
。
（1）∵
，
， ∴
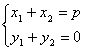
由
，得：
∴
；或
∴
∴M的坐标为(p,0)。
（2）设动点M的坐标为（x,y），则由，得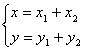
∵ ∴
∴
∴ 
∴
∴
∴动点M的轨迹方程为y2=2p(x-p).
备注：本题还可以利用韦达定理及“差分法”（又称为“设而不求”），思路较广。
21、本题考查导数知识在实际问题中的应用，同时培养学生的动手实践能力。
（1）设切去的正方形的边长为x，则焊接成的长方体的底面边长为4-2x，高为x ,所以
∴
，令
，得：
（舍去）
而
∴当
时，
当
时，
∴
时，
取最大值
。
（2）在正方形的两个角各切下一个边长为1的小正方形，再将其焊接到另一边的中间（两边对应），再将它们焊接成一个长方体，显然此时
符合题意。
22、本题考察函数、数列知识的综合应用，培养分析问题、解决问题的能力。
解：（1）由对任意实数α、β，恒有成立，可得
，故
∴
（2）由
，可得：
∴
,即：
又是正数数列，故
，所以
，即数列是等差数列。
又
，故
。
（3）假设存在等比数列，使得对于一切正整数n都成立，令
，可得
，求得
，
故的公比为2,从而
令
则
故
∴
，故对于一切正整数n都成立。