高考数学热身练习一
一、选择题
1、若
则
的值为
（ ）
A、
B、
C、
D、
2、a、b为实数，集合
表示把集合M中的元素x映射到集合N中仍为x，则
=
（ ）
A、1 B、0 C、－1 D、±1
3、 已知正项等比数列数列{an}，bn=log a an, 则数列{bn}是 （ ）
A、等比数列 B、等差数列 C、既是等差数列又是等比数列 D、以上都不对
4、若函数f(x)的反函数
，则f(2)=（ ）
A、1 B、-1 C、1或-1 D、5
5、条件P：x+1>2，条件Q：
，则P是Q的（ ）
A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既非充分又非必要条件
6、方程a2x2+(a+2)y2+2ax+a=0表示圆，则a的值为（ ）
A、2 B、-1 C、2或-1 D、 不存在
7、从2004名学生中选取50名组成参观团,若采用下面的方法选取: 先用简单随机抽样
从2004人中剔除4人,剩下的2000人再按系统抽样的方法进行.则每人入选的概率（ ）
A、不全相等 B、均不相等 (不做)
C、都相等,且为
D、都相等,且为
8、每个顶点的棱数共有3条的正多面体共有（ ）种
A、2 B、3 C、4 D、5
9、若函数
则
的一个可能的值是（ ）
A、
B、
C、
D、
10、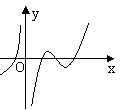
设函数f(x)在定义域内可导，y=f(x)的图象如图1所示，则导函
数y=f ¢(x)可能为（ ）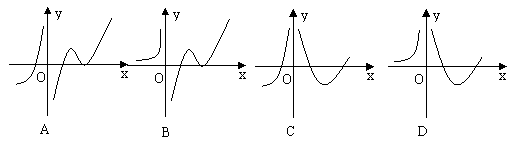
11、已知对称轴为坐标轴的双曲线的两渐近线方程为y=±
x,(a , b>0), 若双曲线上有一点M(x0, y0), 使bx0<ay0,则双曲线的焦点 （ ）
A、在x轴上 B、在y轴上
C、当a>b时在x轴上 D、当a>b时在y轴上
12、某人为了观看2008年奥运会，从2001年起，每年5月10日到银行存入
元定期储蓄，若年利率为p且保持不变，并约定每年到期存款均自动转为新的一年定期，到2008年将所有的存款及利息全部取回，则可取回的钱的总数（元）为
（ ）
A、
B、
C、
D、
13、已知
展开式中x3项的系数是
，则正整数n=
14、椭圆
的两个焦点在圆
上，则此椭圆离心率e=
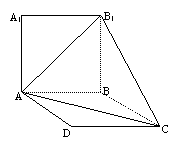
15、如图：棱长为2的正方形ABB1A1与
菱形ABCD所在平面互相垂直，
且
则点A1到面AB1C的距离为
16． 关于曲线
给出下列说法：①关于直线
对称；②关于直线
对称；③关于点
对称；④关于直线
对称；⑤是封闭图形，面积小于
；⑥是封闭图形，面积大于；⑦不是封闭图形，无面积可言.则其中正确说法的序号是
.（注：把你认为正确的序号都填上）
17、已知向量
.
（Ⅰ）若点A、B、C不能构成三角形，求实数m应满足的条件；
（Ⅱ）若△ABC为直角三角形，求实数m的值.
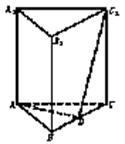
18．如图正三棱柱，棱都相等，D是BC上一点，AD⊥C1D.
（Ⅰ）求证：截面ADC1⊥侧面BCC1B1.
（Ⅱ）求二面角C—AC1—D的大小.
（Ⅲ）若AB=2，求A1B与截面ADC1的距离.
热身练一参考答案：
1.A 2.A 3.B(10) 4.B 5.B 6.B 7.C 8.B 9.A 10.D 11.B 12.D(13)
13、4 14、
15、 (11)
16、①②③⑥
(10)
17、解（Ⅰ）已知向量
若点A、B、C不能构成三角形，则这三点共线，………………2分
…………5分 故知
……7分
∴实数
时，满足的条件…………8分
（Ⅱ）若△ABC为直角三角形，且（1）∠A为直角，则
，
…………10分 解得
…………12分
18．（Ⅰ）证明：易证AD⊥面BB1C1C
∴面ADC1⊥面BB1C1C 4分
（Ⅱ）arcsin
8分
（Ⅲ）
12分