高考数学数列
一)选择题
1.(2004.湖北理)已知数列{![]() }的前n项和
}的前n项和![]() 其中a、b是非零常数,则存在数列{
其中a、b是非零常数,则存在数列{![]() }、{
}、{![]() }使得 ( C )
}使得 ( C )
A.![]() 为等差数列,{
为等差数列,{![]() }为等比数列
}为等比数列
B.![]() 和{
和{![]() }都为等差数列
}都为等差数列
C.![]() 为等差数列,{
为等差数列,{![]() }都为等比数列
}都为等比数列
D.![]() 和{
和{![]() }都为等比数列
}都为等比数列
2. (2004. 重庆理)若![]() 是等差数列,首项
是等差数列,首项![]() ,则使前n项和
,则使前n项和![]() 成立的最大自然数n是: ( C )
成立的最大自然数n是: ( C )
A.4005 B.4006 C.4007 D.4008
3.(2004.湖南理)数列![]() ( C )
( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.(2004.湖南理)农民收入由工资性收入和其它收入两部分构成。2003年某地区农民人均收入为3150元(其中工资性收入为1800元,其它收入为1350元), 预计该地区自2004年起的5 年内,农民的工资性收入将以每年6%的年增长率增长,其它收入每年增加160元。根据以上数据,2008年该地区农民人均收入介于 ( B )
A.4200元~4400元 B.4400元~4600元
C.4600元~4800元 D.4800元~5000元
5、(2004. 人教版理科)设数列![]() 是等差数列,且
是等差数列,且![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和,则( )
项和,则( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
二)填空题
6.(04. 上海春季高考)在数列![]() 中,
中,![]() ,且对任意大于1的正整数
,且对任意大于1的正整数![]() ,点
,点![]() 在直线
在直线![]()
 上,则
上,则![]() _____________.3
_____________.3
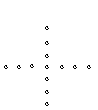 7.(04. 上海春季高考)根据下列5个图形及相应点的个数的变化规律,试猜测第
7.(04. 上海春季高考)根据下列5个图形及相应点的个数的变化规律,试猜测第![]() 个图中有____
个图中有____![]() _______个点.
_______个点.
 | |||||
| |||||
(1) (2) (3) (4) (5)
8.(04. 上海春季高考)在等差数列![]() 中,当
中,当![]()
![]() 时,
时,![]()
必定是常数数列。然而在等比数列![]() 中,对某
中,对某
些正整数![]() 、
、![]()
![]() ,当
,当![]() 时,非常数数
时,非常数数
列![]() 的一个例子是____________.
的一个例子是____________.![]() ,
,![]() 与
与![]() 同为奇数或偶数
同为奇数或偶数
9.设数列{an}的前n项和为Sn,Sn=![]() (对于所有n≥1),且a4=54,则a1的数值是_______________________.2
(对于所有n≥1),且a4=54,则a1的数值是_______________________.2
10、(2004.上海理)设等比数列{an}(n∈N)的公比q=-![]() ,且
,且![]() (a1+a3+a5+…+a2n-1)=
(a1+a3+a5+…+a2n-1)=![]() ,则a1= 2 .
,则a1= 2 .
11、(2004.上海理)若干个能唯一确定一个数列的量称为该数列的“基本量”.设{an}是公比为q的无穷等比数列,下列{an}的四组量中,一定能成为该数列“基本量”的是
第 12、①、④ 组.(写出所有符合要求的组号)
①S1与S2; ②a2与S3; ③a1与an; ④q与an.
其中n为大于1的整数, Sn为{an}的前n项和.
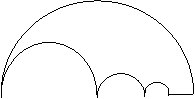
12.(2004. 重庆理)如图P1是一块半径为1的半圆形纸板,在P1的左下端剪去一个半径为![]() 的半圆后得到图形P2,然后依次剪去一个更小半圆(其直径为前一个被剪掉半圆的半径)得圆形P3、P4、…..,Pn,…,记纸板Pn的面积为
的半圆后得到图形P2,然后依次剪去一个更小半圆(其直径为前一个被剪掉半圆的半径)得圆形P3、P4、…..,Pn,…,记纸板Pn的面积为![]() ,则
,则![]() .
.![]()
 |  | ||||||
 |  | ||||||
| |||||||
| |||||||
三)解答题
13.(2004. 辽宁卷)(本小题满分14分)
已知函数![]() 的最大值不大于
的最大值不大于![]() ,又当
,又当![]()
(1)求a的值;
(2)设![]()
13.本小题主要考查函数和不等式的概念,考查数学归纳法,以及灵活运用数学方法分析和
解决问题的能力. 满分14分.
(1)解:由于![]() 的最大值不大于
的最大值不大于![]() 所以
所以
![]() ① ………………3分
① ………………3分
又![]() 所以
所以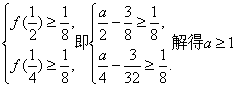 . ②
. ②
由①②得![]() ………………6分
………………6分
(2)证法一:(i)当n=1时,![]() ,不等式
,不等式![]() 成立;
成立;
因![]() 时不等式也成立.
时不等式也成立.
(ii)假设![]() 时,不等式
时,不等式![]() 成立,因为
成立,因为![]() 的
的
对称轴为![]() 知
知![]() 为增函数,所以由
为增函数,所以由![]() 得
得
![]() ………………8分
………………8分
于是有
![]()
…………12分
所以当n=k+1时,不等式也成立.
根据(i)(ii)可知,对任何![]() ,不等式
,不等式![]() 成立.…………14分
成立.…………14分
证法二:(i)当n=1时,![]() ,不等式
,不等式![]() 成立;
成立;
(ii)假设![]() 时不等式成立,即
时不等式成立,即![]() ,则当n=k+1时,
,则当n=k+1时,
![]() ………………8分
………………8分
因![]() 所以
所以
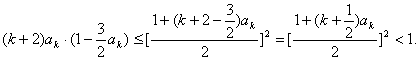 ……12分
……12分
于是![]() 因此当n=k+1时,不等式也成立.
因此当n=k+1时,不等式也成立.
根据(i)(ii)可知,对任何![]() ,不等式
,不等式![]() 成立.…………14分
成立.…………14分
14.(2004.湖南理)(本小题满分14分)
如图,直线![]() 相交于点P.直线l1与x轴交于点P1,过点P1作x轴的垂线交直线l2于点Q1,过点Q1作y轴的垂线交直线l1于点P2,过点P2作x轴的垂线交直线l2于点Q2,…,这样一直作下去,可得到一系列点P1、Q1、P2、Q2,…,点Pn(n=1,2,…)的横坐标构成数列
相交于点P.直线l1与x轴交于点P1,过点P1作x轴的垂线交直线l2于点Q1,过点Q1作y轴的垂线交直线l1于点P2,过点P2作x轴的垂线交直线l2于点Q2,…,这样一直作下去,可得到一系列点P1、Q1、P2、Q2,…,点Pn(n=1,2,…)的横坐标构成数列![]()
(Ⅰ)证明![]() ;
;
(Ⅱ)求数列![]() 的通项公式;
的通项公式;
(Ⅲ)比较![]() 的大小.
的大小.
14.(Ⅰ)证明:设点Pn的坐标是![]() ,由已知条件得
,由已知条件得
点Qn、Pn+1的坐标分别是:
![]()
由Pn+1在直线l1上,得 ![]()
所以 ![]() 即
即 ![]()
(Ⅱ)解:由题设知 ![]() 又由(Ⅰ)知
又由(Ⅰ)知 ![]() ,
,
所以数列 ![]() 是首项为
是首项为![]() 公比为
公比为![]() 的等比数列.
的等比数列.
从而 ![]()
(Ⅲ)解:由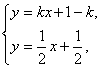 得点P的坐标为(1,1).
得点P的坐标为(1,1).
所以 ![]()
![]()
(i)当![]() 时,
时,![]() >1+9=10.
>1+9=10.
而此时 ![]()
(ii)当![]() 时,
时,![]() <1+9=10.
<1+9=10.
而此时 ![]()
15.(2004. 天津卷)(本小题满分12分)
已知定义在R上的函数![]() 和数列
和数列![]() 满足下列条件:
满足下列条件:
![]() ,
,
![]()
其中![]() 为常数,
为常数,![]() 为非零常数。
为非零常数。
(I)令![]() ,证明数列
,证明数列![]() 是等比数列;
是等比数列;
(II)求数列![]() 的通项公式;
的通项公式;
(III)当![]() 时,求
时,求![]()
15本小题主要考查函数、数列、等比数列和极限等概念,考查灵活应用数学知识分析问题和解决问题的能力。满分12分。
(I)证明:由![]() 可得
可得
![]()
由数学归纳法可证 ![]()
![]()
由题设条件,当![]() 时
时
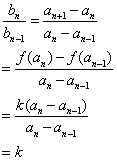
因此,数列![]() 是一个公比为
是一个公比为![]() 的等比数列。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。4分
的等比数列。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。4分
(II)解:由(I)知,![]()
![]()
当 ![]() 时
时
![]()
![]()
当 ![]() 时
时
![]()
![]()
而 ![]()
![]()
所以,当![]() 时
时
![]()
上式对![]() 也成立。所以,数列
也成立。所以,数列![]() 的通项公式为
的通项公式为
![]()
当![]() 时
时
![]()
上式对![]() 也成立。所以,数列
也成立。所以,数列![]() 的通项公式为
的通项公式为
![]() 。
。
(III)解:当![]() 时
时
![]()
![]() 。。。。。。。。。。。。。。。。。。。。。。。。。。。12分
。。。。。。。。。。。。。。。。。。。。。。。。。。。12分
16.(2004.江苏)设无穷等差数列{an}的前n项和为Sn.
(Ⅰ)若首项![]() ,公差
,公差![]() ,求满足
,求满足![]() 的正整数k;
的正整数k;
(Ⅱ)求所有的无穷等差数列{an},使得对于一切正整数k都有![]() 成立.
成立.
16、解:(1)![]()
(2)![]() 或
或![]() 或
或![]()
17.(2004. 福建理)(本小题满分12分)
某企业2003年的纯利润为500万元,因设备老化等原因,企业的生产能力将逐年下降.若不能进行技术改造,预测从今年起每年比上一年纯利润减少20万元,今年初该企业一次性投入资金600万元进行技术改造,预测在未扣除技术改造资金的情况下,第n年(今年为第一年)的利润为500(1+![]() )万元(n为正整数).
)万元(n为正整数).
(Ⅰ)设从今年起的前n年,若该企业不进行技术改造的累计纯利润为An万元,进行技术改造后的累计纯利润为Bn万元(须扣除技术改造资金),求An、Bn的表达式;
(Ⅱ)依上述预测,从今年起该企业至少经过多少年,进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润?
17.本小题主要考查建立函数关系式、数列求和、不等式的等基础知识,考查运用数学知识解决实际问题的能力.满分12分.
解:(Ⅰ)依题设,An=(500-20)+(500-40)+…+(500-20n)=490n-10n2;
Bn=500[(1+![]() )+(1+
)+(1+![]() )+…+(1+
)+…+(1+![]() )]-600=500n-
)]-600=500n-![]() -100.
-100.
(Ⅱ)Bn-An=(500n-![]() -100) -(490n-10n2)
-100) -(490n-10n2)
=10n2+10n-![]() -100=10[n(n+1) -
-100=10[n(n+1) - ![]() -10].
-10].
因为函数y=x(x+1)
-
![]() -10在(0,+∞)上为增函数,
-10在(0,+∞)上为增函数,
当1≤n≤3时,n(n+1)
-
![]() -10≤12-
-10≤12-![]() -10<0;
-10<0;
当n≥4时,n(n+1) - ![]() -10≥20-
-10≥20-![]() -10>0.
-10>0.
∴仅当n≥4时,Bn>An.
答:至少经过4年,该企业进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润.
18.(2004.湖北理)(本小题满分14分)
已知![]()
(I)已知数列![]() 极限存在且大于零,求
极限存在且大于零,求![]() (将A用a表示);
(将A用a表示);
(II)设![]()
(III)若![]() 都成立,求a的取值范围.
都成立,求a的取值范围.
18.本小题主要考查数列、数列极限的概念和数学归纳法,考查灵活运用数学知识分析问题和解决问题的能力,满分14分.
解:(I)由![]()
![]()
(II)![]()
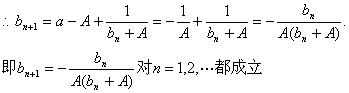
(III)![]()
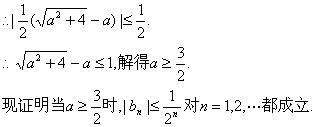
(i)当n=1时结论成立(已验证).
(ii)假设当![]()
![]()
故只须证明![]()
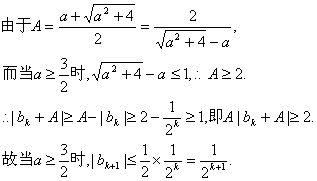
即n=k+1时结论成立.
根据(i)和(ii)可知结论对一切正整数都成立.
故![]()
19. (04. 上海春季高考) (本题满分14分) 本题共有2个小题,第一小题满分6分,第2小题满分8分.
某市2003年共有1万辆燃油型公交车。有关部门计划于2004年投入128辆电力型公交车,
随后电力型公交车每年的投入比上一年增加50%,试问:
(1) 该市在2010年应该投入多少辆电力型公交车?
(2)
到哪一年底,电力型公交车的数量开始超过该市公交车总量的![]() ?
?
19.(1)该市逐年投入的电力型公交车的数量组成等比数列![]() ,其中
,其中![]()
则在2010年应该投入的电力型公交车为![]() (辆)。
(辆)。
(2)记![]() ,依据题意,得
,依据题意,得![]() 。于是
。于是![]() (辆),即
(辆),即![]() ,
,
则有![]() 因此
因此![]() 。所以,到2011年底,电力型公交车的数量开始超过该市公交车总量的
。所以,到2011年底,电力型公交车的数量开始超过该市公交车总量的![]() 。
。