高考数学数列与不等式试题选编
l 数列
(一)选择题、填空题
示例:一张报纸,其厚度为a,面积为b,现将此报纸对折(既沿对边中点的连线折叠)7次,这时报纸的厚度和面积分别是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
答案:C
示例:已知数列![]() 满足
满足![]() 记
记![]() 则下列结论正确的是( )
则下列结论正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
答案:A.
示例:在正数![]() 、
、![]() 之间插入数
之间插入数![]() ,使之成为等差数列,又
,使之成为等差数列,又![]() 、
、![]() 之间插入数
之间插入数![]() 、
、![]() 使之成为等比数列,则有 (
)
使之成为等比数列,则有 (
)
A.![]() C.
C.![]()
C.![]() D.
D.![]()
答案:D
示例:2003年12月,全世界爆发"禽流感",科学家经过深入的研究,终于发现了一种细菌M在杀死"禽流感"病毒N的同时能够自身复制.已知1个细菌M可以杀死1个病毒N,并且生成2个细菌M,那么1个细菌M和2047个"禽流感"病毒N最多可生成细菌M的数值是( )
A. 1024 B. 2047 C. 2048 D. 2049
答案:C.
示例:某班试用电子投票系统选举班干部,全班k名同学都有选举权和被选举权,他们的编号分别为1、2、3、…、k,规定:同意按“1”,不同意(含弃权)按“0”.
令![]() 则同时同意第1、2号同学当选的人数为 ( )
则同时同意第1、2号同学当选的人数为 ( )
A.f(1,1)+f(1,2)+…+f(1, k)+f(2,1)+f(2,2)+…+f(2, k)
B.f(1,1)+f(2,1)+…+f(k,1)+f(1,2)+f(2,2)+…+f(k,2)
C.f(1,1)f(1,2)+f(2,1)f(2,2)+…+f(k,1)f(k,2)
D.f(1,1)f(2,1)+f(1,2)f(2,2)+…+f(1, k)f(2,k)
答案:C.
示例:已知数列{![]() }前n项和
}前n项和![]() 其中b是与n无关的常数,且0<b<1,若
其中b是与n无关的常数,且0<b<1,若![]() 存在,则
存在,则![]() ________.
________.
答案: 1
示例:设数列an的通项公式为
![]() ,试写出一个满足条件的
,试写出一个满足条件的![]() .
.
答案: 不唯一,![]() 的所有实数均可.由
的所有实数均可.由![]()
![]()
示例:如图,第![]() 个图形是由正
个图形是由正![]() 边形“扩展”而来,(
边形“扩展”而来,(![]() 则第
则第![]() 个图形中共有
个顶点.
个图形中共有
个顶点.
|
答案:![]()
示例:计算机执行以下程序
①始值![]() ;
;
②![]() ;
;
③![]() ;
;
④如![]() ,则进⑤行,否则从②继续运行;
,则进⑤行,否则从②继续运行;
⑤打印![]() ;
;
⑥Stop;
那么由语句⑤打印出的数值为 .
答案:91
(二)解答题
示例:化工厂购进了245桶液体工业原料,为了方便保管和运输,要求将它们堆放成纵截面为等腰梯形的一垛,且相邻两层只相差一桶。在不考虑占地面积、堆放高度等具体条件时,堆放方案有哪几种?
答案:d=1,由等差数列前n项和公式可得到![]() 与n的关系:
与n的关系:![]() =
=![]() -
-![]() ,又
,又![]()
![]() 1,所以:n(n+1)
1,所以:n(n+1)![]() 490,而n可取490的不大于21的正整数约数2,5,7,10,14,最后共有五种设计方案:n=2时
490,而n可取490的不大于21的正整数约数2,5,7,10,14,最后共有五种设计方案:n=2时![]() =122;n=5时
=122;n=5时![]() =47;n=7时
=47;n=7时![]() =32;n=10时
=32;n=10时![]() =20;n=14时
=20;n=14时![]() =11.
=11.
示例:设各项均为正数的数列![]() 的前n项和为
的前n项和为![]() ,对于任意的正整数n都有等式
,对于任意的正整数n都有等式![]() 成立.
成立.
(1)求![]() ;
;
(2)求证![]() ;
;
(3)求![]() .
.
答案:(1)当n=1时,![]() .
.
(2)当![]() 时,
时,![]()
![]()
当n=1时,也符合![]()
![]()
(3) 当![]() 时,
时,![]()
![]()
![]() ,
, ![]()
于是数列![]() 是首项为2,公差为2的等差数列.
是首项为2,公差为2的等差数列.
![]() ,
,
![]() ,
,
![]()
![]() .
.
示例:已知函数f(x)= 的图象过原点,以直线x= -1为渐近线,且关于直线x+y=0对称.
(1)求函数f(x)的解析式;
(2)若数列{an}(n∈N*)满足:an>0,a1=1,an+1= [f()]2,求a2,a3,a4的值,猜想数列{an}的通项公式an,并证明你的结论;
(3)若数列{an}的前n项的和为Sn,判断Sn与2的大小关系,并证明你的结论.
答案:(1) ∵函数f(x)= 的图象过原点,即f(0)=0,∴c =0,∴f(x)= .
又函数f(x)= = b - 的图象以直线x= -1为渐近线,且关于直线x+y=0对称,∴函数y=f(x)的图象以(-1,1)为对称中心的双曲线,∴a=1,b=1,∴f(x)= .
(2)由题意有an+1=[ ]2,即 = ,即 = +1,∴ - =1.
∴数列{}是以1为首项,1为公差的等差数列. ∴ =1+(n-1)=n,即 = ,
∴an= .
∴a2= ,a3= ,a4= ,an= .
(3)当n≥2时,an= < = - .
∴Sn= a1 + a2 + a3 + … + an <1+1- + - + - +… + - =2 - <2.
故Sn <2.
示例:数列![]() 中,首项a1=2,前n项和为Sn,对于任意点
中,首项a1=2,前n项和为Sn,对于任意点![]() ,点Pn都在平面直角坐标系xoy的曲线c上,曲线c的方程为
,点Pn都在平面直角坐标系xoy的曲线c上,曲线c的方程为![]() .
.
(1)判断![]() 是否为等比数列,并证明你的结论;
是否为等比数列,并证明你的结论;
(2)若对每个正整数![]() 为边长能构成三角形,求t的范围.
为边长能构成三角形,求t的范围.
答案:(1)由![]()

(2)由(1)知:![]()

示例:已知数列![]() 为直角坐标平面上的点.
为直角坐标平面上的点.
(1)n∈N,点A,Bn,Cn在同一条直线上,求数列{an}的通项公式;
(2)若数列{bn}是首项为-3,公差为3的等差数列,Sn表示△ACnDn的面积,设![]() ,试用n表示Hn;
,试用n表示Hn;
(3)求![]() .
.
答案:(1) ∵对n∈N,点A,Bn,Cn在同一条直线上,
∴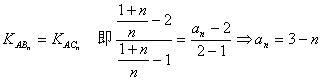 .
.
(2)又数列{bn}是首项为-3,公差为3的等差数列,
∴![]() .
.
△ACnDn的面积![]() .
.
当![]() 且n∈N时,
且n∈N时,![]() ,
,
当![]() .
.
![]() ,
,
所以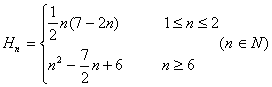 .
.
(3)![]() .
.
l 不等式
(一)选择题、填空题
示例:已知![]() ,不等式
,不等式![]() 的解集是
的解集是![]() ,则
,则![]() 满足的关系是( )
满足的关系是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
答案:C.
示例:某纯净水制造厂在净化水过程中,每增加一次过滤可减少水中杂质20%,要使水中杂质减少到原来的5%以下,则至少需过滤的次数为(参考数据lg2=0.3010,lg3=0.4771)
A. 5 B. 10 C. 14 D. 15
答案:C.
示例:不等式![]() 的解集是_______.
的解集是_______.
答案:![]() .
.
示例:观察下列式子:![]() ,则可以猜想的结论为:___________________________.
,则可以猜想的结论为:___________________________.
答案:![]()
(二)解答题
示例:已知![]() 且
且![]() 试解关于
试解关于![]() 的不等式
的不等式
![]()
答案: 令![]() (
(![]() ) ,
) ,
则原不等式![]() .
.
![]()
即 ![]() ,
,![]()
故当![]() 时,原不等式的解是
时,原不等式的解是![]() 当
当![]() 时,原不等式的解是
时,原不等式的解是![]()
示例:解不等式:![]()
答案:
原不等式可化为![]() 即
即![]()
∵a<1,∵(x-2)![]()
当![]() 时,即0<a<1时,解集为
时,即0<a<1时,解集为![]()
当![]() 时,即a=0时,解集为
时,即a=0时,解集为![]() ;
;
当![]() 时,即a<0时,解集为
时,即a<0时,解集为![]()
示例:(1)已知![]() 是正常数,
是正常数,![]() ,
,![]() ,求证:
,求证:![]() ,指出等号成立的条件;
,指出等号成立的条件;
(2)利用(1)的结论求函数![]() (
(![]() )的最小值,指出取最小值时
)的最小值,指出取最小值时![]() 的值.
的值.
答案:
(1)![]()
![]() ,
,
故![]() .当且仅当
.当且仅当![]() ,即
,即![]() 时上式取等号;
时上式取等号;
(2)由(1)![]() .
.
当且仅当![]() ,即
,即![]() 时上式取最小值,即
时上式取最小值,即![]() .
.
示例:对于定义在区间![]() 上的两个函数
上的两个函数![]() 和
和![]() ,如果对任意的
,如果对任意的![]() ,均有不等式
,均有不等式![]() 成立,则称函数
成立,则称函数![]() 与
与![]() 在
在![]() 上是“友好”的,否则称“不友好”的.现在有两个函数
上是“友好”的,否则称“不友好”的.现在有两个函数![]() 与
与![]()
![]() ,给定区间
,给定区间![]() .
.
(1)若![]() 与
与![]() 在区间
在区间![]() 上都有意义,求
上都有意义,求![]() 的取值范围;
的取值范围;
(2)讨论函数![]() 与
与![]() 在区间
在区间![]() 上是否“友好”.
上是否“友好”.
答案:(1)函数![]() 与
与![]() 在区间
在区间![]() 上有意义,
上有意义,
必须满足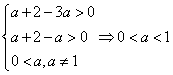
(2)假设存在实数![]() ,使得函数
,使得函数![]() 与
与![]() 在区间
在区间![]() 上是“友好”的,
上是“友好”的,
则![]()
即 ![]() (*)
(*)
因为![]() ,而
,而![]() 在
在![]() 的右侧,
的右侧,
所以函数![]() 在区间
在区间![]() 上为减函数,从而
上为减函数,从而
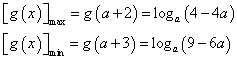
于是不等式(*)成立的充要条件是
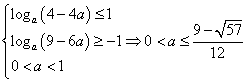
因此,当![]() 时,函数
时,函数![]() 与
与![]() 在区间
在区间![]() 上是“友好”的;当
上是“友好”的;当![]() 时,函数
时,函数![]() 与
与![]() 在区间
在区间![]() 上是不“友好”的.
上是不“友好”的.
示例:已知二次函数![]() 的图像过
的图像过![]() 、
、![]() 两点,且满足
两点,且满足![]() .
.
(1)证明:![]() 或
或![]() ;
;
(2)证明:函数f(x)的图像必与x轴有两个交点;
(3)若关于x的不等式f(x)>0的解集为![]() 或
或![]() (n<m<0),解关于x的不等式
(n<m<0),解关于x的不等式![]() .
.
答案:(1)![]() ,
,
![]() 得
得![]() 、
、![]() .
.
(2)当![]() 时,二次函数f(x)的图像开口向上,图像上的点A、B的纵坐标均为
时,二次函数f(x)的图像开口向上,图像上的点A、B的纵坐标均为![]() 且小于零,所以图像x轴有两个交点;
且小于零,所以图像x轴有两个交点;
当![]() 时,二次函数f(x)的图像开口向下,图像上的点A、B的纵坐标均为
时,二次函数f(x)的图像开口向下,图像上的点A、B的纵坐标均为![]() 且大于零,所以图像x轴有两个交点.
且大于零,所以图像x轴有两个交点.
所以函数f(x)的图像与x轴有两个不同交点.
(3)![]() 的解集为
的解集为![]() 或
或![]() (n<m<0),
(n<m<0),
![]()
从而方程![]() 的两个根为
的两个根为![]() ,
,![]() , 则方程
, 则方程![]() 的两个根为
的两个根为![]() ,
,![]() .
.
因为n<m<0,所以![]() ,
,
故不等式![]() 的解集为
的解集为![]() 或
或![]() .
.
示例:已知二次函数![]() R)满足
R)满足![]() ,对任意实数x,都有
,对任意实数x,都有![]() ,且
,且![]() 时,总有
时,总有![]() .
.
(1)求![]() ;
;
(2)求a,b,c的值;
(3)当![]() ,
,![]() 时,函数
时,函数![]() (m
(m![]() R)是单调函数,求m的取值范围.
R)是单调函数,求m的取值范围.
答案:(1)![]() 对任意实数x,都有
对任意实数x,都有![]() ,所以
,所以![]() ,又
,又![]() 在
在![]() 时,有
时,有![]() ,故
,故![]() ,因此有
,因此有![]() .
.
(2)因为![]() ,
,![]() ,则
,则![]() ,
,![]() ,因为
,因为![]() ,则
,则![]() (当且仅当
(当且仅当![]() 时取等号).又因为对任意实数x,都有
时取等号).又因为对任意实数x,都有![]() ,所以
,所以![]() 恒成立,即
恒成立,即![]() 恒成立
恒成立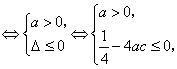 故
故![]() 且
且![]() ,因此有
,因此有![]() ,从而
,从而![]()
![]()
(3)![]()
![]()
![]() ,
,![]() 的对称轴是
的对称轴是![]() ,因为
,因为![]() (m
(m![]() R)在
R)在![]() ,
,![]() 上是单调函数,所以
上是单调函数,所以![]() 或
或![]() .
.