高考数学题预测征题
 例1如图1,过椭圆
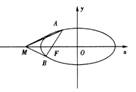
例1如图1,过椭圆![]() 的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在
的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在![]() 轴上,且使得MF为
轴上,且使得MF为![]() 的一条内角平分线,则称点M为该椭圆的“左特征点”.
的一条内角平分线,则称点M为该椭圆的“左特征点”.
(1)求椭圆![]() 的“左特征点”M的坐标;
的“左特征点”M的坐标;
|
椭圆![]() 的“左特征点”M是一个怎样的点?并证明你的结论.
的“左特征点”M是一个怎样的点?并证明你的结论.
解析: (1)设![]() 为椭圆
为椭圆![]() 的左特征点,椭圆的左焦点为
的左特征点,椭圆的左焦点为![]() ,可设直线
,可设直线![]() 的方程为
的方程为![]() .并将它代入
.并将它代入![]() 得:
得:![]() ,即
,即![]() .
.
设![]() ,则
,则![]() ,
,
∵![]() 被
被![]() 轴平分,∴
轴平分,∴![]() .
.
即![]() .
.
即![]() .
.
∴![]() .
.
于是![]() .
.
∵![]() ,即
,即![]() .
.
(2)对于椭圆![]() .于是猜想:椭圆
.于是猜想:椭圆![]() 的“左特征点”是椭圆的左准线与
的“左特征点”是椭圆的左准线与![]() 轴的交点.
轴的交点.
证明:设椭圆的左准线![]() 与
与![]() 轴相交于M点,过A,B分别作
轴相交于M点,过A,B分别作![]() 的垂线,垂足分别为C,D.
的垂线,垂足分别为C,D.
据椭圆第二定义:![]()
∵![]()
![]()
于是![]() 即
即![]() .
.
∴![]() ,又
,又![]() 均为锐角,
均为锐角,
∴![]() ,∴
,∴![]() .
.
∴![]() 的平分线.故M为椭圆的“左特征点”.
的平分线.故M为椭圆的“左特征点”.
点评:近年高考关于圆锥曲线的解答题常作为把关题或压轴题,综合考查考生在数形结合、等价转换、分类讨论、逻辑推理等诸方面的能力.本题背景新颖,而且考查了《考试大纲》所要求的研究性学习能力,是一道压轴题水平的综合能力题.
|
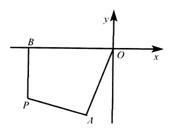 例2如图2,已知过原点O,从
例2如图2,已知过原点O,从(1)求![]() 点的轨迹方程;
点的轨迹方程;
(2)已知点![]() 的轨迹为C,
的轨迹为C,
直线![]() 的斜率为
的斜率为![]() ,若直线
,若直线![]() 与曲线C有两个不同的交点M,N,交线MN的中点为
与曲线C有两个不同的交点M,N,交线MN的中点为![]() ,求点
,求点![]() 的横坐标的取值范围.
的横坐标的取值范围.
解析:(1)设![]() ,
,
![]() 轴,
轴,![]() .又
.又![]() ,
,
![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
![]() ,
,
![]() .
.
由![]() 成等差数列得:
成等差数列得:
![]() .
.
![]() ,即
,即![]() .
.
![]()
![]() 点的轨迹方程为
点的轨迹方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() ,由
,由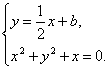 得
得![]() .
.
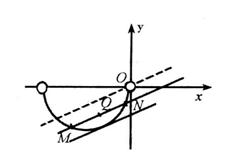 如图3所示,
如图3所示,
|
直线![]() 与圆相切,此时
与圆相切,此时![]() ,注意到
,注意到![]() ,则当
,则当![]() 时,
时,![]() 与圆相切.结合图形得
与圆相切.结合图形得![]() 又
又![]() ,
,![]() .即
.即![]() 点的横坐标的取值范围为
点的横坐标的取值范围为![]() .
.
点评:向量及其运算是新课程的新增内容,由于向量融数,形于一体,具有代数形式和几何形式的双重身份,使它成为中学数学知识的一个交汇点,成为联系多项内容的媒介.本题将向量与解析几何、数列、方程、不等式以及数形结合思想等有机结合,体现了《考试大纲》要求的“在知识网络交汇点处命题”的精神,预测今年的向量高考题的难度可能上升到压轴题水平.
例3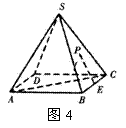 如图4,在正四棱锥S-ABCD
如图4,在正四棱锥S-ABCD
中,E是BC的中点,P点在侧面![]() 内
内
及其边界上运动,并且总是保持PE![]() AC.
AC.
(1)指出动点P的轨迹(即说明动点P在满足给定的条件下运动时所形成的图形),证明你的结论;
(2)以轨迹上的动点P为顶点的三棱锥P-CDE的最大体积是正四棱锥S-ABCD体积的几分之几?
(3)设动点P在G点的位置时三棱锥P-CDE的体积取最大值V1,二面角G-DE-C的大小为![]() ,二面角G-CE-D的大小为
,二面角G-CE-D的大小为![]() ,求
,求![]() 的值.
的值.
 (4)若将“E是BC的中点”改为“E是BC上异于B、C的一定点”,其它条件不变,请指出点P的轨迹,证明你的结论.
(4)若将“E是BC的中点”改为“E是BC上异于B、C的一定点”,其它条件不变,请指出点P的轨迹,证明你的结论.
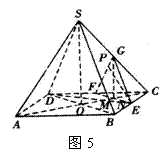
解析:(1)如图5,分别取CD、SC
的中点F、G,连结EF、EG、FG、BD.设
AC与BD的交点为O,连结SO,则动点
P的轨迹是![]() 的中位线FG.
的中位线FG.
由正四棱锥可得![]() .又
.又![]()
![]() 平面EFG,
平面EFG,![]() 平面EFG,
平面EFG,![]() .
.
(2)由于![]() 是定值,所以当P到平面CDE的距离最大时,
是定值,所以当P到平面CDE的距离最大时,![]() 最大,易知当P与G重合时,P到平面CDE的距离最大,故
最大,易知当P与G重合时,P到平面CDE的距离最大,故![]() .又
.又![]() ,G到平面ABCD的距离是点S到平面ABCD的距离的
,G到平面ABCD的距离是点S到平面ABCD的距离的![]() ,
,
![]() .
.
(3)令![]() ,EF与AC交于N点,连结GN,则GN
,EF与AC交于N点,连结GN,则GN![]() 平面ABCD.
平面ABCD.
因此二面角G-DE-C和二面角G-CE-D的平面角的正切值的比就等于N到DE和CE的距离的倒数比.
![]() N是OC的中点,
N是OC的中点,![]() N到BC的距离为
N到BC的距离为![]() .
.
连结DE交OC于M,则M是![]() 的重心,
的重心,![]() .
.
又![]() ,
,
在![]() 中,容易求得N到DE的距离为
中,容易求得N到DE的距离为![]() .
.
故![]() .
.
(4)动点P在侧面SCD内部及其边界上运动,且总保持![]() ,那么这些相交于定点E的直线系应位于某个与直线AC垂直的平面内,而由正四棱锥的性质可知,
,那么这些相交于定点E的直线系应位于某个与直线AC垂直的平面内,而由正四棱锥的性质可知,![]() 平面SBD,因此动直线PE集中在过E且平行于平面SBD的一个平面内.过E作E
平面SBD,因此动直线PE集中在过E且平行于平面SBD的一个平面内.过E作E![]() //SB,E
//SB,E![]() //BD,分别交SC于
//BD,分别交SC于![]() ,交CD于
,交CD于![]() ,则平面E
,则平面E![]() //平面SBD,从而
//平面SBD,从而![]() 平面E
平面E![]() ,故点P的轨迹是线段
,故点P的轨迹是线段![]() .
.
点评:本题全方位地考查了立体几何中的主要内容,如线面与线线的位置关系、体积问题、二面角问题等.在立体几何的问题中给出了探求点的轨迹问题,与平面几何、解析几何紧密联系,体现了对综合运用知识的能力要求,考查的知识点丰富,具有相当的难度和深度,达到了压轴题的水平,是一道创新型试题.
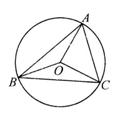 例4已知O是锐角三角形ABC的外心,
例4已知O是锐角三角形ABC的外心,![]() 的面积数依次成等差数列.
的面积数依次成等差数列.
(1)推算![]() 是否为定值?说明理由;
是否为定值?说明理由;
(2)求证:![]() 也成等差数列.
也成等差数列.
|
则![]() ,
,
同理:![]() .
.
![]() 成等差数列,
成等差数列,
![]()
即![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
又![]() ,故
,故![]() .
.
![]() .
.
又![]() ,
,
![]() .
.
整理得 ![]() .
.
(1)因![]() 是锐角三角形,
是锐角三角形,![]() ,可知
,可知![]() ,
,
![]() ,
,
故![]() 为定值.
为定值.
(2)![]()
![]() .
.
![]() ,
,
即![]() 成等差数列.
成等差数列.
点评:这是一道探索性试题,它涉及到圆的性质、等差数列的性质、三角形的边角关系、三角形的面积公式、三角函数的恒等变形等知识.问题的关键在于如何将面积关系![]() 转化为角
转化为角![]() 、
、![]() 、
、![]() 的关系,转化的桥梁便是三角形的面积公式及正弦定理.
的关系,转化的桥梁便是三角形的面积公式及正弦定理.