高考数学应试选择题百题训练

高考数学应试选择题百题训练

1、同时满足① M{1, 2, 3, 4, 5}; ② 若a∈M，则(6-a)∈M, 的非空集合M有（　）。

  （A）16个　 （B）15个　 （C）7个　 （D）8个

　提示：着重理解“∈”的意义，对M中元素的情况进行讨论，分别讨论“一个、两个、三个、四个、五个元素”等几种情况，得出相应结论。

2、函数y=f (x)是R上的增函数，则a+b>0是f (a)+f (b)>f (-a)+f (-b)的（　）条件。

  （A）充分不必要　 （B）必要不充分　 （C）充要　 　　 （D）不充分不必要

提示：由a>-b 以及 y = f ( x )在R上为增函数可知：f ( a )  > f ( b ) ，f ( b )  > f ( - a )，反过来，由增函数的概念也可推出，a+b>（-a）+（-b）。

 3、函数g(x)=x²，若a≠0且a∈R, 则下列点一定在函数y=g(x)的图象上的是（ 　）。

  （A）(-a, -g(-a)) （B）(a, g(-a)) （C）(a, -g(a)) （D）(-a, -g(a))

  提示：本题从函数的奇偶性入手。

4、数列{a_n}满足a₁=1, a₂=，且 (n≥2)，则a_n等于（ 　）。

  （A）　（B）()^n-1　（C）()ⁿ　（D）

  提示：用验证法筛选可得。

5、由1，2，3，4组成的没有重复数字的四位数，按从小到大的顺序排成一个数列{a_n}，其中a₁₈等于（　）。　　　　 （A）1243　 （B）3421　 （C）4123　 （D）3412

提示：用间接法，由大到小排列。

 6、若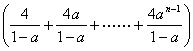=9，则实数a等于（ 　）。

  （A）　 （B）　 （C）-　 （D）-

提示：运用无穷递缩等比数列的求和公式。

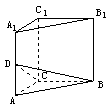
  7、已知圆锥内有一个内接圆柱，若圆柱的侧面积最大，则此圆柱的上底面将已知圆锥的体积分成小、大两部分的比是（ 　）。　　 （A）1:1　 （B）1:2　 （C）1:8　 （D）1:7

提示：运用图象，帮助解题。

  8、下列命题中，正确的是（ 　）。

  （A）y=arccosx是偶函数　（B）arcsin(sinx)=x, x∈R

  （C）sin(arcsin)=　　（D）若-1<x<0, 则-<arcsinx<0

　 提示：反三角函数的概念、公式的理解与运用。

9、函数y=f (x)的反函数f ^-1(x)= (x∈R且x≠-3)，则y=f (x)的图象（ 　）。

  （A）关于点(2, 3)对称　　  （B）关于点(-2, -3)对称

  （C）关于直线y=3对称　　（D）关于直线x=-2对称

提示：主要考核反函数的概念与对称性的知识。

10、两条曲线y=与x = -的交点坐标是（ 　）。

  （A）(-1, -1)　 （B）(0, 0)和(-1, -1)　　（C）(-1, 1)和(0, 0)　 （D）(1, -1)和(0, 0)

　 提示：从定义域、值域、特殊值等角度加以验证。

11、已知a, b∈R, m=, n=-b+b²，则下列结论正确的是（ 　）。

  （A）m<n　 （B）m≥n　 （C）m>n　 （D）m≤n

  提示：由题意可知m≤、 n=(b-1) ² +。

12、正方体ABCD-A₁B₁C₁D₁中，EF是异面直线AC、A₁D的公垂线，则EF和BD₁的关系是（ 　）。

  （A）垂直　（B）平行　（C） 异面　（D）相交但不垂直

　提示：理解公垂线的概念，通过平行作图可知。

13、直线4x+6y-9=0夹在两坐标轴之间的线段的垂直平分线是l，则l的方程是（   ）。

  （A）24x-16y+15=0　 （B）24x-16y-15=0　 （C）24x+16y+15=0　 （D）24x+16y-15=0

　提示：通过两线垂直与斜率的关系，以及中点坐标公式。

14、函数f (x)=log_a(ax²-x)在x∈[2, 4]上是增函数，则a的取值范围是（   ）。

  （A）a>1　 （B）a>0且a≠1　 （C）0<a<1　 （D）a∈

　提示：分类讨论，考虑对称轴与单调区间的概念。

15、函数y=cos²(x-)+sin²(x+)-1是（ 　）。

  （A）周期为2π的奇函数　 （B）周期为π的偶函数

（C）周期为π的奇函数　　 （D）周期为2π的偶函数

提示：用倍角公式化简。

 16、若a, b∈R，那么成立的一个充分非必要条件是（   ）。

  （A）a>b　 （B）ab(a-b)<0　 （C）a<b<0　 （D）a<b

　提示：理解条件语句，用不等式的性质解题。

17、函数y=cos⁴x-sin⁴x图象的一条对称轴方程是（   ）。

  （A）x=-　 （B）x=-　 （C）x= 　（D）x=

　提示：先降次，后找最值点。

18、已知l、m、n为两两垂直且异面的三条直线，过l作平面α与m垂直，则直线n与平面α的关系是（   ）。

  （A）n//α　 （B）n//α或nα　 （C）nα或n不平行于α　 （D）nα

　提示：画草图，运用线面垂直的有关知识。

19、若z₁, z₂∈C，z₁=z₂=1且arg(z₁)=150°, arg(z₂)=300°，那么arg(z₁+z₂)为（   ）。

  （A）450°　 （B）225°　 （C）150°　 （D）45°

　提示：旋转与辐角主值的概念。

20、已知a、b、c成等比数列，a、x、b和b、y、c都成等差数列，且xy≠0，那么的值为（   ）。

  （A）1　 （B）2　 （C）3　 （D）4

  提示：运用等比、差中项概念，通分求解。

21、如果在区间[1, 3]上，函数f (x)=x²+px+q与g(x)=x+在同一点取得相同的最小值，那么下列说法不对的是（   ）。　（A）f (x)≥3 (x∈[1, 2])　　　　（B）f (x)≤4 (x∈[1, 2])　

　　　　　　　　　  （C）f (x)在x∈[1, 2]上单调递增　 （D）f (x)在x∈[1, 2]上是减函数

　提示：通过最值定理、二次函数的对称轴与最值等求出p 、q，再行分析。

22、在(2+)¹⁰⁰展开式中，有理数的项共有（   ）。

  （A）4项　 （B）6项　 （C）25项　 （D）26项

  提示：借助二项式展开的通项公式来分析。

23、在正四棱柱ABCD－A₁B₁C₁D₁中，M为AD中点，O为侧面AA₁B₁B的中心，P为侧棱CC₁上任意一点，那么异面直线OP与BM所成的角是（   ）。

  （A）90°　 （B）60°　 （C）45°　 （D）30°

  提示：运用平行和垂直的有关知识。

24、等比数列{a_n}的公比q<0，前n项和为S_n, T_n=，则有（   ）。

  （A）T₁<T₉　（B）T₁=T₉　（C）T₁>T₉　（D）大小不定

　提示：T₁=1，用等比数列前n项和公式求T₉

25、设集合A＝，集合B＝{0}，则下列关系中正确的是（　 ）

　 （A）A＝B  （B）AB　　（C）AB　 （D）AB　

  提示：主要考核空集的概念、以及集合与集合的关系。

26、已知直线l过点M（－1，0），并且斜率为1，则直线l的方程是（　 ）

（A）　　　　　　　　 x＋y＋1＝0　（B）x－y＋1＝0　

（C）x＋y－1＝0　 （D）x―y―1＝0

  提示：直线方程的点斜式。

27、已知α－β＝,tgα=3^m, tgβ=3^－m, 则m的值是（　 ）。

  （A）2　（B）－　（C）－2　（D）

  提示：通过tanαtanβ= 1，以及tan（α－β）的公式进行求解。

28、已知集合A＝{整数}，B＝{非负整数}，f是从集合A到集合B的映射，且f：x y＝x²（x∈A，y∈B），那么在f的作用下象是4的原象是（　 ）

　 （A）16　（B）±16　（C）2　（D）±2

  提示：主要考核象和原象的概念。

29、有不等式① cos<cos0.7；② log_0.50.7<log₂；③ 0.5^0.7<2^1.5；④ arctg<arctg。其中成立的是（ 　）。

 （A）仅①②　（B）仅②③　（C）仅③④　（D）①②③④

  提示：主要考核三角函数、对数、指数函数、反三角函数的知识。

30、已知函数y＝,那么（　 ）

 （A）当x∈（－∞，1）或x∈（1，＋∞）时，函数单调递减

  （B）当x∈（－∞，1）∪（1，＋∞）时，函数单调递增

 （C）当x∈（－∞，－1）∪（－1，＋∞）时，函数单调递减

 （D）当x∈（－∞，－1）∪（－1，＋∞）时，函数单调递增

  提示：先对函数式进行变形，再运用有关大小比较的知识解题。

 31、若－π≤2α≤π,那么三角函数式化简为（　 ）

　 （A）sin　（B）－sin　（C）cos　（D）－cos　

提示：主要运用半角公式及三角函数单调性等知识。

32、如图，在直三棱柱ABC－A₁B₁C₁中，底面ABC是等腰直角三角形，斜边AB＝a，侧棱AA₁=2a,点D是AA₁的中点，那么截面DBC与底面ABC所成二面角的大小是（　 ）

（A）　　30°　（B）45°　（C）60°　（D）非以上答案

  　提示：实际上是要求角DCA的大小。

33、加工某一机械零件，需要经过两个工序，完成第一个工序有3种不同的方法，完成第二个工序有4种不同的方法，那么加工这一零件不同的方法种数有（　 ）

　 （A）12种　（B）7种　（C）4种　（D）3种

   提示：运用乘法原理解题。

34、在(2－)⁸的展开式中，第七项是（　 ）

  （A）112x³ （B）－112x³ （C）16x³（D）－16x³　

　 提示：运用二项展开式的通项公式，注意：r =6。

35、在－8，－6，－4，－2，0，1，3，5，7，9这十个数中，任取两个作为虚数a＋b的实部和虚部（a, b∈R, a≠b），则能组成模大于5的不同虚数的个数有（　 ）。

　 （A）64个　（B）65个　（C）72个　（D）73个

　 提示：虚部不能为0，模大于5，最好用“树图”来讨论。

36、直线x－ay＋＝0（a>0且a≠1）与圆x²＋y²＝1的位置关系是（　 ）

　 （A）相交　（B）相切　（C）相离　（D）不能确定

提示：运用点到直线的距离公式，比较半径与距离的大小。

37、在正方体AC₁中，过与顶点A相邻的三个顶点作平面α，过与顶点C₁相邻的三个顶点作平面β，那么平面α与平面β的位置关系是（　 ）

　 （A）垂直　（B）平行　（C）斜交　（D）斜交或平行

　　提示：作图后，找线线关系，由线线平行得出线面平行，从而求得面面平行。

38、有下列三个对应：①A＝R^＋，B＝R，对应法则是“取平方根”；②A＝{矩形},B＝R^＋，对应法则是“求矩形的面积”；③A＝{非负实数}，B＝（0，1），对应法则是“平方后与1的和的倒数”，其中从A到B的对应中是映射的是（　 ）。

　 （A）② （B）②，③　（C）①，②，③　（D）①，②

  提示：映射的概念。

39、设A＝{x x²＋px＋q＝0},B＝{x x²＋(p－1)x＋2q＝0},若A∩B＝{1}，则（　 ）。

（A）　　　　　　　　 AB　（B）AB　

（C）A∪B ＝{1, 1, 2} （D）A∪B＝(1,－2)

  提示：考察集合与集合的关系。

40、能够使得sinx>0和tgx>0同时成立的角x的集合是（　 ）。　（A）{x0<x<} 　　　　

（B）{x0<x<或<x<}（C）{x<x<＋,k∈Z} （D）{x2<x<2＋,k∈Z}

  提示：通过不同象限，三角函数值的正负不同的特点，进行分析。

41. 已知函数y＝＋cos(2x＋), (≤x≤), 下列关于此函数的最值及相应的x的取值的结论中正确的是（　 ）。

　 （A）y_max＝，x＝  （B）y_max＝，x＝

   （C）y_min＝，x＝　　　（D）y_min＝0，x＝

提示：对余弦函数最值进行分析。

 42、已知函数f（x）在定义域R内是减函数且f（x）<0，则函数g(x)＝x² f（x）的单调情况一定是（　 ）。

　 （A）在R上递减　　　　　 （B）在R上递增　

　 （C）在（0，＋∞）上递减　 （D）在（0，＋∞）上递增　

　　提示：先选定区间（0，＋∞）分析其增减性，再结合筛选法，对余下的部分，取特殊值进行验证。

43、α，β是两个不重合的平面，在α上取4个点，在β上取3个点，则由这些点最多可以确定平面（　 ）。

　 （A）35个　（B）30个　（C）32个　（D）40个

  提示：运用排列组合以及平面的性质进行分析。

44、已知定点P₁（3，5），P₂（－1，1），Q（4，0），点P分有向线段所成的比为3，则直线PQ的方程是（　 ）。

（A）　　　　　　　　 x＋2y－4＝0　（B）2x＋y－8＝0　

（C）x－2y－4＝0　　　 （D）2x－y－8＝0

提示：用定比分点坐标公式求P点坐标，再考察PQ的斜率。

45、函数y=x在[－1, 1]上是（   ）。

  （A）增函数且是奇函数　 （B）增函数且是偶函数

  （C）减函数且是奇函数　 （D）减函数且是偶函数

提示：运用函数奇偶性的定义，以及奇函数在不同区间上增减性一致，偶函数在不同区间上不一致的特点，进行分析。

46、下列函数中，在[,π]上是增函数的是（   ）。

  （A）y=sinx　 （B）y=cosx　 （C）y=sin2x　 （D）y=cos2x

  提示：用图象法解题。

47、与函数y=sin(arcsinx)的图象相同的的是（   ）。

  （A）y=x　 （B）y=arcsin(sinx)　

（C）y=arccos(cosx)　 （D）y=cos(arccosx)

  提示：考虑函数的定义域与值域。

48、方程cosx=lgx的实根的个数是（ 　）。

  （A）1个　 （B）2个　 （C）3个　 （D）4个

提示：用图象法解题。

  49、一个首项为23，公差为整数的等差数列，如果前6项均为正数，第7项起为负数，则它的公差是（   ）。

  （A）－2　 （B）－3　 （C）－4　 （D）－5

提示：分析前6项为正，第7项起为负数。列出不等式解题。

  50、已知复数z满足2z－i=2，则z＋2i的最小值是（   ）。

  （A）　 （B）　 （C）1　 （D）2

  提示：数形结合，通过图象解题。

51、正三棱锥的侧棱长和底面边长比值的取值范围是（   ）。

  （A）[, ＋∞]　 （B）(, ＋∞)　

（C）[, ＋∞]　 （D）(, ＋∞)

提示：画图形，侧棱应比底边三角形的外接圆的半径大。

52、已知椭圆(a>b>0)的离心率等于，若将这个椭圆绕着它的右焦点按逆时针方向旋转后，所得的新椭圆的一条准线的方程y=，则原来的椭圆方程是（   ）。

  （A）　（B）　

（C）　（D）

  提示：旋转的过程中，焦点到准线的距离没有变，先找焦点。

53、直线x－y－1=0与实轴在y轴上的双曲线x²－y²=m (m≠0)的交点在以原点为中心，边长为2且各边分别平行于坐标轴的正方形内部，则m的取值范围是（   ）。

  （A）0<m<1　 （B）m<0　 （C）－1<m<0　 （D）m<－1

提示：通过极限位置，找出相关范围。

54、已知直线l₁与l₂的夹角的平分线为y=x，如果l₁的方程是ax＋by＋c=0(ab>0)，那么l₂的方程是（   ）。

  （A）bx＋ay＋c=0　 （B）ax－by＋c=0　

（C）bx＋ay－c=0　 （D）bx－ay＋c=0

  提示：联系反函数的概念。

55、函数F(x)=(1＋)f (x) (x≠0)是偶函数，且f (x)不恒等于零，则f (x)（   ）。

  （A）是奇函数　　  　　　　　　　（B）是偶函数

  （C）可能是奇函数，也可能是偶函数 （D）非奇、非偶函数

  提示：先讨论y=(1＋)的奇偶性，再结合题目中的已知内容分析。

56、函数y=的反函数（ 　 ）。

  （A） 是奇函数，它在(0, ＋∞)上是减函数

  （B）是偶函数，它在(0, ＋∞)上是减函数

  （C）是奇函数，它在(0, ＋∞)上是增函数

  （D）是偶函数，它在(0, ＋∞)上是增函数

　提示：先对给出函数进行分析，再运用反函数的概念解题。

57、若a, b是任意实数，且a>b，则（ 　 ）。

  （A）a²>b²　（B）<1　（C）lg(a－b)>0　（D）()^a<()^b

　提示：运用平方数、分数、对数、指数函数的概念进行分析。

58、若log_a2<log_b2<0，则（   ）。

  （A）0<a<b<1　 （B）0<b<a<1　 （C）a>b>1　 （D）b>a>1

　提示：先确定对数符号（即真数和底数与1的关系一致时（同时大于或同时小于），为正，不一致时，为负。）再用换底公式。

59、已知等差数列{a_n}的公差d≠0，且a₁, a₃, a₉成等比数列，则的值是（   ）。

  （A）　 （B）　 （C）　 （D）

提示：先求a₁和公比的关系，再化简。

 60、如果α, β∈(, π)，且tgα<ctgβ，那么必有（   ）。

  （A）α<β （B）β<α （C）α＋β< （D）α＋β>

提示：先用诱导公式化成同名函数，再借助函数图象解题。

　61、已知集合Z={θ cosθ<sinθ, 0≤θ≤2π}, F={θ tgθ<sinθ}，那么Z∩F的区间（   ）。

  （A）(, π)　 　　　（B）(, )　

（C）(π, )　 　　（D）(, )

　　提示：用图象法解题。

62、如果直线y=ax＋2与直线y=3x＋b关于直线y=x对称，那么（   ）。

  （A）a=, b=6　 （B）a=, b=－6　

（C）a=3, b=－2　 （D）a=3, b=6

　提示：运用反函数的知识。

63、已知f()=，则f (x)=（   ）。

  （A）(x＋1)² 　　　　（B）(x－1)²　

（C）x²－x＋1　 　　（D）x²＋x＋1

　提示：用换元法。

64、若函数f (x)=的定义域是R，则实数k的取值范围是（   ）。

  （A）[0, ]　 （B）(－∞, 0)∪(, ＋∞)　

（C）[0, ]　 （D）[, ＋∞]

　提示：分母不为0，用根的判别式。

65、设P是棱长相等的四面体内任意一点，则P到各个面的距离之和是一个定值，这个定值等于（   ）。

  （A）四面体的棱长　 （B）四面体的斜高

 （C）四面体的高　　　　（D）四面体两对棱间的距离

　提示：用体积求。

66、若正四棱柱的底面积为P，过相对两侧棱的截面面积是Q，则该四棱柱的体积是（   ）。

  （A）Q　 （B）P　 （C）Q　 （D）P

提示：化面积为边。

 67、过定点(1, 3)可作两条直线与圆x²＋y²＋2kx＋2y＋k²－24=0相切，则k的取值范围是（   ）。

  （A）k>2　 （B）k<－4　 （C）k>2或k<－4　 （D）－4<k<2

　提示：画定点、平移圆、定区域。

68、适合z－2=1且argz=的复数z的个数是（   ）。

  （A）0　 （B）1　 （C）2　 （D）3

　提示：在直角坐标系中画圆，找出适合条件的复数。

69、已知{a_n}是等比数列，且a_n>0, a₂a₄＋2a₃a₅＋a₄a₆=25，那么a₃＋a₅的值为（   ）。

  （A）5　 （B）10　 （C）15　 （D）20

　提示：用等比的性质：若数列为等比数列，m+m=k+l时，a_m a_n= a_k a_l 。

70、设a, b是满足ab<0的实数，那么（ 　 ）。

　　（A）a＋b>a－b　　  （B）a＋b<a－b　

　（C）a－b<a－b　　（D）a－b<a＋b

　提示：从符号出发，取特殊值代入。

71、如果AC<0且BC<0, 那么直线Ax＋By＋C=0不通过（ 　 ）。

  （A）第一象限　 （B）第二象限　

（C）第三象限　 （D）第四象限

　提示：分析符号，找斜率和截距。

72、直线的倾斜角是（   ）。

  （A）20°　 （B）70°　 （C）110°　 （D）160°

　提示：化参数方程为普通方程。

73、函数y=sinxcosx＋sinx＋cosx的最大值是（ 　 ）。

  （A）　（B）　（C）1＋　（D）＋

　提示：用倍角公式和（sinx＋cosx）的公式。

74、函数y=0.2^x＋1的反函数是（ 　 ）。

（A）　　　　　　　　 y=log₅x＋1　（B）y=log_x5＋1

（C）y=－log₅(x－1) （D）y=－log₅x－1

　提示：反函数的定义，结合定义域、值域的变换情况进行讨论。

75、设α、β都是第二象限的角，若sinα>sinβ，则（ 　 ）。

（A）　　　　　　　　 tgα>tgβ　（B）ctgα<ctgβ　

（C）cosα>cosβ　（D）secα>secβ

提示：结合特殊值，找出α、β在[0，2π]上的大小关系。

76、下列命题：① 函数y=tgx是增函数；② 函数y=sinx在第一象限是增函数；③ 函数y=3sin(2x＋5θ)的图象关于y轴对称的充要条件是θ=, k∈Z；④ 若角α是第二象限的角，则角2α一定是第四象限的角。其中正确命题的个数是（ 　 ）。

  （A）0个　 （B）1个　 （C）2个　 （D）3个

　提示：紧扣定义，逐个分析。

77、在△ABC中，A>B是cos2B>cos2C的（ 　 ）。

  （A）非充分非必要条件　 （B）充分非必要条件

  （C）必要非充分条件　　 （D）充要条件

提示：分若三种情况，取特殊值验证。

78、若0<a<b<1，则下列不等式成立的是（ 　 ）。

  （A）logb<a^b<log_ba　  （B）logb <log_ba<a^b　

  （C）log_ba< logb<a^b　 （D）a^b< logb <log_ba

提示：运用对数符号确定的有关知识，先讨论两个对数值，然后用指数。

79、要使sinα－cosα=有意义，则m的取值范围是（   ）。

（A）　　　　　　　　 m≤　（B）m≥－1　

（C）－1≤m≤　（D）m≤－1或 m≥

　提示：先对等式左边进行变形，再对分数变形。

80、直线xcosθ－y＋1=0的倾斜角的范围是（ 　 ）。

  （A）[－, ]　　　　  （B）[, ]

  （C）(0, )∪(, π)　 （D）[0, ]∪[, π]

　提示：先讨论斜率，再用三角函数的知识。

81、设n≥2时，数列的和是（ 　 ）。

  （A）0　 （B）(－1)ⁿ2ⁿ　 （C）1　 （D）

提示：特殊值法。

 82、在四棱锥的四个侧面中，直角三角形最多可有（ 　 ）。

  （A）1个　 （B）2个　 （C）3个　 （D）4个

提示：用图形来验证。　

83、当z=时，z¹⁰⁰＋z⁵⁰＋1的值等于（ 　 ）。

  （A）1　 （B）－1　 （C）i　 （D）－I

提示：先化Z为三角形式，然后用棣莫佛定理。

 84、函数y=的值域是（ 　 ）。

  （A）{－2, 4}　　　　 （B）{－2, 0, 4}　

（C）{－2, 0, 2, 4}　　　 （D）{－4, －2, 0, 4}

提示：分象限讨论。

 85、正三棱锥S－ABC的侧棱与底面边长相等，如果E、F分别是SC、AB的中点，那么异面直线EF、SA所成的角为（ 　 ）。

  （A）90°　 （B）60°　 （C）45°　 （D）30°

提示：巧用中位线平行于底边。

 86、若正棱锥的底面边长与侧棱相等，则该棱锥一定不是（ 　 ）。

  （A）三棱锥　（B）四棱锥　（C）五棱锥　（D）六棱锥

　提示：用射影和直角三角形的知识。

87、四边形ABCD是边长为1的正方形，E、F为BC、CD的中点，沿AE、EF、AF折成一个四面体，使B、C、D三点重合，这个四面体的体积为（ 　 ）。

  （A）　 （B）　 （C）　 （D）

　提示：分析图形的折叠与边角关系。

88、一束光线从点A(－1, 1)出发经x轴反射，到达圆C：(x－2)²＋(y－3)²=1上一点的最短路程是（ 　 ）。

  （A）4　 （B）5　 （C）3－1　 （D）2

　提示：用对称性，找关于X轴对称的圆心位置，用两点间距离减半径。

89、设地球半径为R，当人造地球卫星距离地面的高度为h₁与h₂时，可以直射到地表面的面积分别是地球表面面积的与，则h₁－h₂等于（ 　 ）。

  （A）R　 （B）R　 （C）R　 （D）2R

　提示：用球冠公式。

90、函数f (x)=x－x－3在定义域内（ 　 ）。

 （A）最大值为3，最小值为－3 （B）最大值为4，最小值为0

 （C）最大值为1，最小值为1 （D）最大值为3，最小值为－1

提示：用区间分析法。

91、如果sinαsinβ=1，那么cos(α＋β)等于（ 　 ）。

  （A）－1　 （B）0　 （C）1　 （D）±1

提示：用公式。

 92、已知α=arg(2＋i), β=arg(－3＋i)，则α－β为（ 　 ）。

  （A）　 （B）　 （C）－　 （D）－

提示：用旋转的方法，进行向量合成。

 93、若双曲线x²－y²=1右支上一点P(a, b)到直线y=x的距离为，则a＋b的值是（ 　 ）。

  （A）－  （B） （C）－或 （D）2或－2

　提示：先确定P点在坐标系中的位置，然后用筛选法。

94、一球内切于一圆台，若此圆台的上、下底面半径分别是a, b，则此圆台的体积是（ 　 ）。

  （A）π(a²＋ab＋b²)　 （B）(a²＋ab＋b²)

  （C）(a²＋ab＋b²)ab　　 （D）(a²＋ab＋b²)

提示：画轴截面，分析平面图形。

　95、若全集I＝R，A＝{x ≤0}，B＝{x lg(x²－2)>lgx}，则A∩＝（ 　 ）。

  （A）{2}　 （B）{－1}　 （C）{x x≤－1}　 （D）

　 提示：先用筛选法，再用验证法。

96、已知函数f (x)=a^x－(b＋2) (a>0, a≠1)的图象不在二、四象限，则实数a, b的取值范围是（ 　 ）。

（A）　　　　　　　　 a>1, b=－1（B）0<a<1, b=－1

（C）a>1, b=－2 （D）0<a<1, b=－2

提示：先分析b，再考虑a。

　97、设函数f (x)=(x∈R, x≠－，)则f ^-1(2)=（ 　 ）。

  （A） －　（B）　 （C）　 （D）－

　提示：令f (x)= 2，求x。

98、如果α, β∈(, π)，且tgα<ctgβ，那么必有（ 　 ）。

  （A）α<β（B）β<α （C）α＋β<（D）α＋β>

提示：用诱导公式，取特殊值。

 99、函数y=sinxcosx＋cos²x－的最小正周期等于（ 　 ）。

  （A）π　 （B）2π　 （C）　 （D）

提示：先用倍角公式降次，合并，再用周期公式。

 100、函数y=－ctgx, x∈(0, π)的反函数为（ 　 ）。

  （A）y=－arctgx　 （B）y=＋arctgx

  （C）y=π－arctgx　 （D）y=π＋arctgx

　提示：运用反三角函数的值域进行分析。

101、设a, b是满足ab<0的实数，那么（ 　 ）。

  （A）a＋b>a－b（B）a＋b<a－b

（C）a－b<a－b（D）a－b>a＋b

　提示：特殊值法。

102、设a, b, c∈R^＋，则三个数a＋, b＋, c＋（ 　 ）。

  （A）都不大于2　　　　　 （B）都不小于2

  （C）至少有一个不大于2　 （D）至少有一个不小于2

　提示：反证法。

103、若一数列的前四项依次是2，0，2，0，则下列式子中，不能作为它的通项公式的是（ 　 ）。

  （A）a_n= 1－(－1)ⁿ　　 （B）a_n=1＋(－1)^n＋1　

  （C）a_n=2sin²　　　（D）a_n=(1－cosnπ)＋(n－1)(n－2)

　提示：验证法。

104、复数z₁=－2＋i的辐角主值为θ₁，复数z₂=－1－3i辐角主值为θ₂，则θ₁＋θ₂等于（ 　 ）。

  （A）　 （B）　 （C）　 （D）

　提示：辐角主值的概念。

105、平行六面体ABCD－A₁B₁C₁D₁的体积为30，则四面体AB₁CD₁的体积是（ 　 ）。

  （A）15　 （B）7.5　 （C）10　 （D）6

　提示：体积公式。

106、不论k为何实数，直线(2k－1)x－(k＋3)y－(k－11)=0恒通过一个定点，这个定点的坐标是（ 　 ）。

  （A）(5, 2)　 （B）(2, 3)　 （C）(5, 9)　 （D）(－,3)

　提示：对原式进行变形。

107、方程ax＋by＋c=0与方程2ax＋2by＋c＋1=0表示两条平行直线的充要条件是（ 　 ）。

  （A）ab>0, c≠1　 （B）ab<0, c≠1　

（C）a²＋b²≠0, c≠1　 （D）a=b=c=2

　提示：两直线平行的充要条件。

108、与三条直线y=0, y=x＋2, y=－x＋4都相切的圆的圆心是（ 　 ）。

(A)　(1, 2＋2)　（B）(1, 3－3)

（C）(1, 3－3)　（D）(1, －3－3)

　提示：用点到直线的距离公式进行验证。

109、焦距是10，虚轴长是8，过点(3, 4)的双曲线的标准方程是（　）。

  （A） （B）

（C） （D）

　提示：运用概念进行验证。

110、函数y=log₃(x²＋x－2)的定义域是（　）。

  （A）[－2, 1]　　　　　　　  （B）(－2, 1)

  （C）(－∞, －2)∪(1, ＋∞)　 （D）(－∞, －2)∪[1, ＋∞]

　提示：解不等式。

111、若log_m0.7>log_n0.7>0，则m, n的大小关系是（　）。

  （A）m>n>1　 （B）n>m>1　 （C）0<n<m<1　 （D）0<m<n<1

　提示：先用对数符号的确定，再用换底公式。

112、函数y=sin(ωx)cos(ωx) (ω>0)的最小正周期是4π，则常数ω为（　）。

  （A）4　 （B）2　 （C）　 （D）

　提示：先用倍角公式，再用周期公式。

113、若(1－2x)⁷=a₀＋a₁x＋a₂x²＋a₃x³＋……＋a₇x⁷，那么a₁＋a₂＋a₃＋……＋a₇的值等于（　）。

  （A）－2　 （B）－1　 （C）0　 （D）2

　提示：取x =1。

114、当A=20°,B=25°时，(1＋tgA)(1＋tgB)的值是（　）。

  （A）　 （B）2　 （C）1＋　 （D）2＋

　提示：公式变形。

115、满足z＋25i≤15的辐角主值最小的复数z是（　）。

  （A）10i　 （B）25i　 （C）－12－16i　 （D）12＋16i

　提示：画圆找切线。

116、圆x²＋y²=1上的点到直线3x＋4y－25=0的距离的最小值是（　）。

  （A）6　 （B）4　 （C）5　 （D）1

　提示：点到直线距离减半径。

117、函数y=cos(－2x)的单调递减区间是（　）。

  （A）[2kπ－, 2kπ＋], k∈Z　　　（B）[kπ＋, kπ＋], k∈Z

  （C）[2kπ＋, 2kπ＋], k∈Z　　 （D）[kπ－, kπ＋], k∈Z

　提示：图象法。

118、已知a, b是两个不等的正数，P=(a＋)(b＋), Q=(＋)², R=(＋)², 那么数值最大的一个是（　）。

  （A）P　 （B）Q　 （C）R　 （D）与a, b的值有关

　提示：特殊值验证法。

119、关于x的方程=kx＋2有唯一解，则实数k的取值范围是（　）。

  （A）k=±　　　　　 （B）k<－2或k>2

  （C）－2<k<2　　　　  （D）k<－2或k>2或k=±

提示：分析圆和直线相切的情况。

120、满足{1, 2}T{1, 2, 3, 4,}的集合T的个数是（　）。

  （A）1　　 （B）2　　 （C）3　　 （D）4

提示：从组合的角度分析题目。

121、若函数y＝f (x)的定义域是(0, 2)，则函数y＝f (－2x)的定义域是（　）。

  （A）(0, 2)　 （B）(－1, 0)　 （C）(－4, 0)　 （D）(0, 4)

提示：理解“定义域”的内涵。

122、已知f (xⁿ)＝lgx，那么f (2)等于（　）。

  （A）lg2　 （B）lg2　 （C）nlg2　 （D）2ⁿlg2

  提示：指数与对数互化。

123、已知m>n>1, 0<a<1，下列不等式不成立的是（　）。

  （A）log_ma>log_na　 （B）a^m>aⁿ　

（C）a^m<aⁿ　 　　 （D）log_am<log_an

  提示：指数函数与对数函数的增减性。

124、设函数y＝f (x)是偶函数，则函数y＝af (x)＋x² (a∈R)的图象关于（　）。

  （A）x轴对称　 （B）y轴对称　

（C）原点对称　 （D）直线y＝x对称

  提示：偶函数的有关知识。

125、条件甲：；条件乙：，则甲是乙的（　）。

  （A）充要条件　　　　　 （B）充分而不必要条件

  （C）必要而不充分条件　 （D）既不充分也不必要条件

  提示：从解集的大小来分析条件命题。

126、已知函数y＝f (x)的定义域是[a, b]，且b>－a>0，则函数F(x)＝f (x)＋f (－x)的定义域是（　）。

  （A）[a, b] （B）[－b, －a] （C）[a, －a] （D）[－b, b]

提示：函数奇偶性的前提条件以及公共区域的有关知识。

 127、“log₃x²＝2”是“log₃x＝1”成立的（　）。

  （A）充要条件　　　　　 （B）必要而不充分条件

  （C）充分而不必要条件　 （D）既不充分也不必要条件

　 提示：对数的真数要为正。

128、设a, b∈R，则不等式a>b, 同时成立的充分必要条件是（　）。

（A）a>b>0或b<a<0 （B）a>0, b<0 （C）b<a<0 （D）0<b<a

  提示：特殊值法。

129、三个数, , 的大小顺序是（　）。

  （A）<<　 （B）<<

  （C）<<　 （D）<<

  提示：幂函数、指数函数的大小比较。

130、若0<a<1, 0<b<1，四个数a＋b, 2, 2ab, a²＋b²中最大者与最小者分别记为M和m，则（　）。

  （A）M＝a＋b, m＝2ab　　　　  （B）M＝a²＋b², m＝2

  （C）M＝a＋b, m＝2　　  （D）M＝a²＋b², m＝2ab

  提示：特殊值法。

131、设lg²x－lgx－2＝0的两根是α、β，则log_αβ＋log_βα等于（　）。

  （A）1　 （B）－2　 （C）3　 （D）－4

　 提示：换底公式与韦达定理。

 132、若y＝f (x)是周期为t的函数，则y＝f (2x＋1)是（　）。

  （A）周期为t的周期函数　　（B）周期为2t的周期函数

  （C）周期为的周期函数　 （D）不是周期函数

　提示：紧扣周期函数的概念。

133、已知y＝f (x)为偶函数，定义域是(－∞, ＋∞)，它在[0, ＋∞)上是减函数，那么m＝f (－)与n＝f (a²－a＋1) (a∈R)的大小关系是（　）。

  （A）m>n　 （B）m≥n　 （C）m<n　 （D）m≤n

　提示：配方以及偶函数在不同区间上的增减性不同。

134、给关于x的不等式2x²＋ax<a² (a≠0)提供四个解，①当a>0时， －a<x<；②当a>0时，－<x<a；③当a<0时，<x<－a；④当a<0时，a<x<－。那么原不等式的解为（　）。

  （A）②或③　（B）①或③ （C）①或④ 　（D）②或④

　提示：解方程，结合二次函数图象分析。

135、已知定义在实数集上的函数y＝f (x)满足f (x＋y)＝f (x)＋f (y), 且f (x)不恒等于零，则y＝f (x)是（　）。

  （A）奇函数　 　　　（B）偶函数　

（C）非奇非偶函数　 （D）不能确定

提示：先求出y＝f (0)= 0，得f (x)+f (-x)=0 。

 136、已知f (x)＝2x＋3, g(x)＝4x－5, f [p(x)]＝g(x)，则p(3)的值是（　）。

  （A）2　 （B）±2　 （C）－2　 （D）不能确定

　提示：结合内外层函数的知识，运用代入法。

137、如果log₂[log(log₂x)]＝ log₃[log(log₃y)]＝ log₅[log(log₅z)]＝0，则有（　）。

  （A）z<x<y　 （B）x<y<z　 （C）y<z<x　 （D）z<y<x

提示：由外向内逐步代入。

 

138、若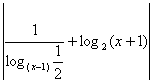<2，那么x的取值范围是（　）。

  （A）(1, ＋∞)　 （B）(1, 2)∪(2, ＋∞)　

（C）(, 2)　 （D）(, 2)∪(2, ＋∞)

　提示：先用换底公式对绝对值里的式子进行化简，再解绝对值不等式。

139、lg9·lg11与1的大小关系是（　）。

  （A）lg9·lg11>1　 （B）lg9·lg11＝1　

（C）lg9·lg11<1　 （D）不能确定

提示：lg10·lg10＝1

 140、方程x²－3x＋2＝0 (x∈R)的根有（　），

  （A）4个　　 （B）3个　　 （C）2个　　 （D）1个

　提示：先把x作为一个整体，再分析。

141、若{a_n}是等比数列，a₄a₇＝－512, a₃＋a₈＝124, 且公比q是整数，则a₁₀等于（　）。

  （A）256　 （B）－256　 （C）512　 （D）－512

　提示：用等比数列的性质，求出q与a₁ 。

142、已知数列{2n－11}，那么有最小值的S_n是（　）。

  （A）S₁　　 （B）S₅　　 （C）S₆　　 （D）S₁₁

  提示：先求最大非正项。

143、若a>0且a≠1，P＝log_a(a³＋1)，Q＝log_a(a²＋1)，则P、Q的大小关系是（　）。

  （A）P>Q　 （B）p<Q　 （C）P＝Q　 （D）不确定

  提示：分类讨论，用指数函数的增减性。

144、如果x_n=(1－)(1－)(1－)……(1－)，则x_n等于（　）。

  （A）0　（B）1　（C）　（D）不确定

提示：交错项相约。

145、数列的通项公式是a_n＝(1－2x)ⁿ，若a_n存在，则x的取值范围是（　）。

  （A）[0, ]　（B）[0, -]　（C）[0, 1]　（D）[0,- 1]

  提示：极限的概念。

146、已知等差数列{a_n}的首项a₁＝120, d＝－4，若S_n≤a_n (n>1)，则n的最小值是（　）。

  （A）60　 （B）62　 （C）63　 （D）70

  提示：运用通项公式与前n项的和公式，列不等式求解。

147、设arg(z)＝θ (0<θ<π)，则arg()等于（　）。

  （A）4π－2θ （B）－2θ （C）2π－2θ （D）2θ

  提示：特殊值法。

148、要使复数z＝(＋i)³(cosθ＋isinθ)所对应的点在复平面的第四象限内，那么θ的取值范围是（　）。

（A）第一象限（B）第二象限（C）第三象限（D）第四象限

  提示：先化成复数三角形式，再用旋转的方法求解。

149、方程z²z＋z²－z²－z＝0在复数集内的解集在复平面上的图形是（　）。

（A）n个点 （B）单位圆 （C）n条直线 （D）原点和单位圆

  提示：提取“公因式”。

150、已知f (n)＝iⁿ－i^-n (i²＝－1, n∈N)，则集合{f (n)}的元素的个数是（　）。

  （A）2　 （B）3　 （C）无数个　（D）以上答案都不对

  提示：分类讨论。n = 4k、4k+1、4k+2、4k+3。

151、若ω是1的n次虚根，则ω＋ω²＋ω³＋……＋ω^n-1的值是（　）。

  （A）n－1　 （B）n　 （C）－1　 （D）0

提示：（ω＋ω²＋ω³＋…＋ω^n-1+ωⁿ ）-（1+ω＋ω²＋ω³＋…＋ω^n-1 ）

 152、不等式x²－x＋1>0的解集是（　）。

  （A）{x x<或x>}　 （B）R　

（C）　　　　　　　　　 （D）以上都不对

提示：解方程。

 153、若复数1＋2i的辐角主值为α，3－4i的辐角主值为β，则2α－β的值为（　）。

  （A）－　 （B）－π　 （C）　 （D）π

  提示：求1＋2i的平方除3－4i所得复数的辐角主值。

154、已知方程x²＋(k＋2i)x＋2＋ki＝0至少有一个实根，那么实数k的取值范围是（　）。

  （A）k≥2或k≤－2　（B）－2≤k≤2

 （C）k＝±2　　　　　  （D）k＝2

  　提示：运用复数相等的定义解题。

155、已知集合P＝{x (x－1)(x－4)≥0}，Q＝{n (n＋1)(n－5)≤0, n∈N}与集合S，且S∩P＝{1, 4}，S∩Q＝S，那么集合S的元素的个数是（　）。

（A）　　2个 　　（B）2个或4个

（B）　　 　　　　（C）2个或3个或4个 （D）无穷多个

　　提示：从自然数的角度分析。

156、有四位司机，四位售票员分配到四辆公共汽车上，使每辆车分别有一位司机和一名售票员，则可能的分配方案数是（　）。

  （A）　　（B）　　（C）　　（D）

　　提示：分步实施。

157、有4个学生和3名教师排成一行照相，规定两端不排教师，那么排法的种数是（　）。

  （A）　 （B）　 （C）　 （D）

　　提示：定位排列。

 158、在1，2，3，4，9中任取两个数分别作对数的底和真数，可得不同的对数值的个数是（　）。

  （A）9　　 （B）12　　 （C）16　　 （D）20

　　提示：1不能为底，注意2、4；3、9！

159、下列等式中，不正确的是（　）。

  （A）(n＋1)＝　　　 （B）　

 （C）＝(n－2)!　　　 （D）＝

　　提示：排列、组合数计算公式。

160、在(1＋2x－x²)⁴展开式中，x⁷的系数是（　）。

  （A）－8　 （B）12　 （C）6　 （D）－12

　　提示：二项展开式的通项公式。

161、如果(1＋x)³＋(1＋x)⁴＋(1＋x)⁵＋……＋(1＋x)⁵⁰＝a₀＋a₁x＋a₂x²＋……＋a₅₀x⁵⁰，那么a₃等于（　）。

  （A）2　　（B）　　（C）　　（D）

　　提示：分别从3、4、5……50个中取3求和。

162、2⁹⁹除以9的余数是（　）。

  （A）0　　 （B）1　　 （C）－1　　 （D）8

　提示：原式可化为（9-1）³³ 。

163、如果x∈(0,2π)，函数y＝的定义域是（　）。

  （A）{x 0<x<π}　　　　（B）{x <x<π}　

 （C）{x <x<2π}　 （D）{x <x≤π}

提示：分象限，定符号。

 

164、化简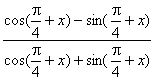的结果是（　） 。

  （A）－tgx　 （B）tg　 （C）tg2x　 （D）ctgx

　提示：分子分母同除cos(+x)，然后用1= tan解题。

165、下列函数中，图象关于坐标原点对称的是（　）。

（A）　　 y＝－sinx 　（B）y＝x·sinx

 （C）y＝sin(－x)　 （D）y＝sinx

提示：奇函数的图象关于原点成对称。

 166、如果函数y＝f (x)的图象关于坐标原点对称，那么它必适合关系式（　）。

  （A）f (x)＋f (－x)＝0　　　　 （B）f (x)－f (－x)＝0

  （C）f (x)＋f ^－1(x)＝0　　　　 （D）f (x)－f ^－1(x)＝0

  提示：奇函数的图象关于原点成对称。

167、θ在第二象限，且＝－cos，则在（　）。

 （A）第一象限　 　 （B）第二象限　

（C）第三象限　 　（D）第四象限

　提示：先讨论可能的范围，再结合象限确定角的符号。

168、若0<α<，则必有（　）。

（A）　　　　　　　　 tg2α>tgα　（B）ctg2α>ctgα

（C）cos2α>cosα　　（D）sec2α>secα

  提示：特殊值法，注意角的符号。

169、画在同一坐标系内的曲线y＝sinx与y＝cosx的交点坐标是（　）。

  （A）(2nπ＋, 1), n∈Z　　 （B）(nπ＋, (－1)ⁿ), n∈Z

  （C）(nπ＋, ), n∈Z　 （D）(nπ, 1), n∈Z

　提示：用图象法解题。

170、若sinα＋cosα＝，则tgα＋ctgα的值是（　）。

　（A）1　 （B）2　 （C）－1　 （D）－2

　提示：特殊值法。

171、三个数a＝arcsin, b＝arctg, c＝arccos(－)的大小关系是（　）。

　（A）c<a<b  （B）c<b<a  （C）a<b<c  （D）b<a<c

　提示：化成同一种反三角函数，再讨论。

172、下列函数中，最小正周期是π的函数是（　）。

　（A）f (x)＝　　　　（B）f (x)＝

　（C）f (x)＝cos²－sin²　　（D）f (x)＝2sin² (x－)

提示：用三角公式化简。

173、在△ABC中，sinBsinC＝cos²，则此三角形是（　）。

　（A）等边三角形　　　　（B）三边不等的三角形

　（C）等腰三角形　　　　（D）以上答案都不对

　提示：cos= sin(B+C)/2。

174、函数y＝arccos(2sinx)的定义域是（　）。

　（A）[－, ]　　　　 （B）[kπ＋, kπ＋], k∈Z

（C）[kπ－, kπ＋], k∈Z （D）[kπ＋, kπ＋], k∈Z

　提示：反三角函数的定义域与三角函数的取值范围。

175、不等式arccos(1－x)<arccosx的解集是（　）。

　（A）0≤x<　（B）0≤x<1　（C）x<　（D）0<x<

　提示：结合反余弦的图象分析。

176、下列各式中，正确的是（　）。

　（A）arcsin(－)＝－　　  （B）arcsin(sin)＝－

　（C）sin(arccos)＝　　 （D）sin(arcsin)＝

　提示：反三角函数的有关公式。

177、下列各命题中，正确的是（　）。

　（A）若直线a, b异面，b, c异面，则a, c异面

　（B）若直线a, b异面，a, c异面，则b, c异面

　（C）若直线a//平面α，直线b平面α，则a//b

　（D）既不相交，又不平行的两条直线是异面直线

　提示：分多种情况作图分析。

178、斜棱柱的矩形面(包括侧面与底面)最多共有（　）。

　（A）2个　 （B）3个　 （C）4个　 （D）6个

　提示：斜棱柱的侧棱与底面的关系。

179、夹在两平行平面之间的两条线段的长度相等的充要条件是（　）。

　（A）两条线段同时与平面垂直　 （B）两条线段互相平行

　（C）两条线段相交　　（D）两条线段与平面所成的角相等

提示：考虑“等价性”。

 180、如果正三棱锥的侧面都是直角三角形，则侧棱与底面所成的角θ应属于下列区间（　）。

　（A）(0, ) （B）(, ) （C）(, ) （D）(, )

　提示：特殊值法结合射影的知识。

181、正方体ABCD－A₁B₁C₁D₁中BC₁与对角面BB₁D₁D所成的角是（　）。

　（A）∠C₁B₁D₁  　　 （B）∠C₁B₁D

 （C）∠C₁B₁B　　　 （D）以上都不是

　提示：线与面所成的角。

182、平面α与平面β平行，它们之间的距离为d (d>0)，直线a在平面α内，则在平面β内与直线a相距2d的直线有（　）。

　（A）一条　（B）二条 （C）无数条 （D）一条也没有

　提示：作图分析。

183、互不重合的三个平面可能把空间分成（　）部分。

（A）　　4或9　　　　　　 （B）6或8　

（B）　　 （C）4或6或8　 （D）4或6或7或8

　提示：化体为面，化面成线。

184、若a, b是异面直线，aα,bβ,α∩β＝c，那么c（　）。

　（A）同时与a, b相交　　　　 （B）至少与a, b中一条相交

　（C）至多与a, b中一条相交　 （D）与a, b中一条相交, 另一条平行

提示：异面直线的概念。

185、直线a//平面M，直线bM, 那么a//b是b//M的（　）条件。

（A）　　 充分不必要 　　（B）必要而不充分

（C）充要　　　　　  （D）不充分也不必要

　提示：线面平行、线线平行的知识。

186、和空间不共面的四个点距离相等的平面的个数是（　）。

　（A）7个　 （B）6个　 （C）4个　 （D）3个

提示：平行底面与分隔顶点。

 187、正方体ABCD－A₁B₁C₁D₁中，与AD₁成60°的面对角线共有（　）。

　（A）10条　 （B）8条　 （C）6条　 （D）4条

　提示：用平移的方法。

188、在长方体相交于一个顶点的三条棱上各取一个点，那么过这三点的截面一定是（　）。

　（A）三角形或四边形　　　　　　　　　 （B）锐角三角形

　（C）锐角三角形或钝角三角形　　　　　 （D）钝角三角形

 

提示：运用三棱锥的有关知识。

189、圆锥底面半径为r，母线长为l，且l>2r, M是底面圆周上任意一点，从M拉一条绳子绕侧面转一周再回到M，那么这条绳子的最短长度是（　）。

　（A）2πr　 （B）2l　 （C）2lsin　 （D）lcos

　提示：用平面展开图。

190、α、β是互不重合的两个平面，在α内取5个点，在β内取4个点，这些点最多能确定的平面个数是（　）。

　（A） 142　（B）72　 （C）70　 （D）66

提示：先不分条件进行组合，然后去除不符合条件的。

191、圆台的轴截面面积是Q，母线与下底面成60°角，则圆台的内切球的表面积是（　）。

　（A）　 （B）Q　 （C）Q　 （D）Q

　提示：利用轴截面求圆台的高。

192、直线＝－1在y轴上的截矩是（　）。

　（A）2　 （B）3　 （C）－2　 （D）－3

提示：化成直线方程的一般式。

193、若直线y＝x＋b和半圆y＝有两个不同的交点，则b的取值范围是（　）。

 （A）(－, ) 　　　　　　（B）[－, ]

（C）(－∞,－)∪[, ＋∞]  （D）[1, ]

  提示：图象法。

194、函数y＝2sin(arccosx)的图象是（　）。

  （A） 椭圆　　（B）半椭圆　　（C）圆　 （D）直线

  提示：先对三角关系式进行变形。

195、各点坐标为A(1, 1)、B(－1, 1)、C(－1, －1)、D(1, －1)，则“点P在y轴”是“∠APD＝∠BPC”的（　）。

　（A）充分而不必要条件　 （B）必要而不充分条件

　（C）充要条件　　　　　 （D）不充分也不必要条件

提示：利用四点共圆的有关知识。

 196、函数y＝1－x－x²的图象大致是（　）。

 （A）　　　　  （B）　　　　 （C）　　　　　 （D）

提示：区间分析法或特殊值法。

197、已知函数y＝ax＋b和y＝ax²＋bx＋c (a≠0)，则它们的图象可能是（　）。

　　（A）　　　　 （B）　　　　（C）　　　　　（D）

  提示：从对称轴、顶点、截距等方面考虑。

198、点A(t, 2^t)关于直线x＋y＝0的对称点的坐标是（　）。

 （A）(t, －2^t) （B）(－t, 2^t) （C）(2^t, －t) （D）(－2^t, －t)

  提示：利用关于x＋y＝0的对称点的特点。

199、已知两圆的方程x²＋y²＝4和x²＋y²－6x＋8y－24＝0，则此两圆的位置关系是（　）。

  （A）外离　　（B）外切　　（C）相交　　（D）内切

  提示：找圆心和半径，用两点间距离公式，注意内切的情况。

200、圆的一条直径的两个端点分别是(2, 0)和(2, －2)，则此圆的方程是（　）。

  （A）x²＋y²－4x＋2y＋4＝0　　（B）x²＋y²－4x－2y－4＝0

  （C）x²＋y²－4x＋2y－4＝0　　（D）x²＋y²＋4x＋2y＋4＝0

  提示：先考虑半径和圆心。

201、双曲线9y²－x²－2x－10＝0的渐近线方程是（　）。

（A）　　　　　　　　 y＝±3(x＋1) （B）y＝±3(x－1)

（C）y＝±(x＋1) （D）y＝±(x－1)

  提示：先化成标准形式，再将1换成0，找渐近线。

202、设F是椭圆的右焦点，P(x, y)是椭圆上一点，则FP等于（　）。

  （A）ex＋a　 （B）ex－a　 （C）ax－e　 （D）a－ex

　提示：椭圆的定义：1、到两定点距离之和等于定值（大于两定点之和）的点的轨迹；2、到定点和定直线（交替）距离之比等于定值（小于1）的点的轨迹。

203、已知M＝{(x, y) y≥x²}，N＝{(x, y) x²＋(y－a)²≤1}，那么使M∩N＝N成立的充要条件是（　）。

  （A）a≥　 （B）a＝　（C）0<a<1　　（D）a≤1

  提示：圆在抛物线内，代入后，用根的判别式法。

204、椭圆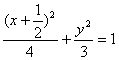与抛物线y²＝6x－9的公共点的个数是（　）。

  （A）0个　　（B）1个　　（C）2个　　（D）3个

  提示：图象或代入验证法。

205、直线l：(x＋y)＋1＋a＝0与圆C：x²＋y²＝a (a>0)的位置关系是（　）。

  （A）恒相切 （B）恒相交 （C）恒相离 （D）相切或相离

  提示：根的判别式法。

206、曲线y＝－与曲线y＋ax＝0 (a∈R)的交点个数一定是（　）。

  （A）2个 （B）4个　（C）0个　（D）与a的取值有关

　提示：取特殊值法。

207、若F(c, 0)是椭圆的右焦点，F与椭圆上点的距离的最大值为M，最小值为m，则椭圆上与F点的距离等于的点的坐标是（　）。

  （A）(c, ±)　 　（B）(－c, ±)　

（C）(0, ±b)　 　 （D）不存在

　提示：先考虑M+m = 2a，然后用验证法。

208、顶点在点(1, 3)，焦点与顶点的距离为，准线平行于y轴，开口向右的抛物线的方程是（　）。

  （A）y－3＝(x－1)²　　　　  （B）(x－1)²＝(y－3)

  （C）(y－3)²＝(x－1)　　　　（D）x－1＝(y－3)²

　提示：坐标平移的有关知识。

209、如果抛物线y²－mx－2y＋4m＋1＝0的准线与双曲线x²－3y²＝12的左准线重合，则m的值为（　）。

  （A）28　　  （B）14　　  （C）－2　　  （D）4

　提示：先求准线，再求焦点。

210、已知方程＝1的图象是双曲线，则m的取值范围是（　）。

  （A）m<1　　 　　（B）m>2　　

（C）1<m<2　　 　（D）m<1或m>2

　提示：双曲线的定义。

211、在同一极坐标系中，点(ρ, θ)与点(－ρ, －θ)的位置关系是（　）。

  （A）关于极轴所在直线对称　 （B）关于极点对称

  （C）重合　　　　　  （D）关于直线θ＝(ρ∈R)对称

　 提示：先定点，再考虑。

 212、极坐标系中，方程ρ＝asinθ (a>0)的图形是（　）。

　 （A）　　 （B）　（C）　 （D）

　提示：极坐标方程的化简。

213、由方程x－1＋y－1＝1确定的曲线所围成的图形的面积是（　）。

  （A）1　　 （B）2　　 （C）π　　 （D）4

　提示：先画图，后分析。

214、若mn<0，则方程mx²－my²＝n所表示的曲线是（　）。

  (A)焦点在x轴上的等轴双曲线　 (B) 圆

  (C)焦点在y轴上的等轴双曲线　 (D)等轴双曲线，焦点位置依m, n的符号而定

  提示：两边同除n，再找实轴。

215、某林场原有森林木材存量为a，木材以每年25%的增长率增长，而每年冬天需砍伐木材量为x，为了实现经过20年达到木材存量至少翻两番的目标，且每年尽可能多提供木材，则x的最大值是（　）。(取lg2＝0.3)

  （A）a　（B）a　（C）a　（D）a

  提示：找等量关系式，注意区分变量与定量。

216、在复平面上，复数z满足arg(z＋3)＝，则的最大值是（　）。

  （A）　 （B）　 （C）　（D）与z的辐角有关

　提示：化求最大值为考虑最小值。

217、将y＝的图象向下平移5个单位，向右平移5个单位后，与原函数的反函数的图象重合，则m的值是（　）。

  （A）6　　  （B）－2　　  （C）5　　  （D）1

提示：把握图象平移与变量的关系，结合反函数的求法解题。

  218、某抛物线型拱桥的跨度是20米，拱高是4米，在建桥时，每隔4米需用一根柱子支撑，其中最长的柱子的高是（　）。

  （A）1.48 米 （B）2.92米　（C）3.84米　（D）4米

  提示：在扇形中，解三角形。

219、将一半径为R的木球加工成一正方体木块，则木块的最大体积是（　）。

  （A）　（B）　（C）　（D）

  提示：球内接正方体的体积，用轴截面的知识。

220、要得到函数f (x)＝cos(2x－)的图象，只需将函数y＝sin2x的图象（　）。

  （A）向右平移个单位　 （B）向右平移个单位

  （C）向左平移个单位　 （D）向右平移个单位

  提示：三角函数的图象平移。

221、无穷数列{}的各项和为（　）。

  （A）　 （B）　 （C）　 （D）不存在

提示：写出该数列的前n项。

 222、若极限(a²－2a)ⁿ存在，则实数a的取值范围是（　）。

  （A）(1－, 1＋)　　　（B）(1－, 1)∪(1, 1＋)

  （C）[1－, 1]∪(1, 1＋) （D）[1－, 1＋]

  提示：解不等式 a²－2a小于1。

223、已知菱形ABCD的边长是1，∠DAB＝60°，将这个菱形沿AC折成120°的二面角，则BD两点间的距离是（　）。

  （A）　 （B）　 （C）　 （D）

  提示：用菱形性质和余弦定理。

224、正三棱锥底面边长为a，侧棱与底面成60°角，过底面一边作截面，使其与底面成30°角，则截面在底面的射影面积为（　）。

  （A）3a²　 （B）2a²　 （C）a²　 （D）a²

  提示：先筛选，再验证。

225、设有四个不同的红球、六个不同的白球，每次取出四个球，取出一个红球记2分，取出一个白球记1分，使得总分不小于5分，共有的取球方法数是（　）。

  （A）　 （B）　

 （C）　 　　　　（D）3

  提示：分类、分步讨论。

226、已知(1＋2x)ⁿ的展开式中，所有项的系数之和等于6561，那么这个展开式中x³的系数是（　）。

  （A）56　 （B）448　 （C）1120　 （D）170

  提示：先求n，再用通项分式求解。

227、常数c使sin(x＋c)＝cos(π＋x)和tg(c－x)＝－ctg(π－x)对于定义域内的一切实数x同时成立，则c的一个值为（　）。

  （A）　 （B）－　 （C）－π　 （D）－

  提示：用验证法。

228、设f (x)＝x＋1，那么f (x＋1)关于直线x＝2对称的曲线方程是（　）。

  （A）y＝x－6　 　 （B）y＝6＋x　

（C）y＝6－x　 　 （D）y＝－x－2

  提示：取特殊点。

229、已知集合A＝{1，2，3，4，5}，B＝{6，7，8}，从A到B的映射f中，满足f (1)≤f (2)≤f (3)≤f (4)≤f (5)的映射有（　）。

  （A）27　 （B）9　 （C）21　 （D）12

  提示：对函数取值的情况进行讨论。

230、若S_n表示等差数列{a_n}的前n项和，已知S₉＝18, S_n＝24，若a_n－4＝30，则n等于（　）。

  （A）15　 （B）16　 （C）17　 （D）18

  提示：用通项、求和公式验证。

 231、现有男女学生共8人，从男生中选2人，从女生中选1人分别参加数学、物理、化学三科竞赛，共有90种不同的方案，那么男、女生人数分别是（  ）。

  （A）男生2人，女生6人　 （B）男生3人，女生5人

  （C）男生5人，女生3人　 （D）男生6人，女生2人

　提示：用验证法。

232、已知集合A＝{x x²－3x＋2＝0}，B＝{x x²－x＋2＝0}，若A∪B＝A，则由a的值组成的集合是（　）。

  （A）{a a＝9} 　　　（B）{a a<8}

（C）{a a<8或a＝9} （D）{a 0≤a<8或a＝9}

　提示：要考虑B是空集的情况。

233、函数y＝sin(－2x)＋sin2x的最小正周期是（　）。

  （A）　 （B）　 （C）π　 （D）2π

　提示：对绝对值符号内的式子进行变形或先不考虑绝对值，再减半。

234、“ab<0”是“不等式a－b≤a＋b的等号成立”的（　）。

（A）　　 充分条件　　　 （B）必要条件

（C）充要条件　　　　（D）不充分也不必要条件

　提示：后面不等式恒成立。

235、用0，1，2，3，4这五个数字可组成没有重复数字且个位数字不是2的不同的五位偶数有（　）。

  （A）24个　 （B）42个　 （C）48个　 （D）60个

　提示：先定个位，再考虑首位。

236、复平面内，向量对应的复数为－＋i，将其绕原点逆时针旋转，再将模伸长2倍，得到向量，则对应的复数是（　）。

  （A）－2i　 　　　（B）－6－2i　

（C）－6＋2i　　　（D）6－2i

　提示：将旋转与向量运算联系起来。

237、设(1－x)¹⁰＝a₀＋a₁x＋a₂x²＋……＋a₁₀x¹⁰，其中a₀, a₁, a₂,……是常数，则(a₀＋a₂＋……＋a₁₀)²－(a₁＋a₃＋……＋a₉)²等于（　）。

  （A）2＋　 （B）　 （C）　 （D）1

　提示：用平方差公式，取x=1，x= -1。

238、若x²＋y²－2x－2y－3＝0，则2x＋y－1的最小值是（　）。

  （A）0　 （B）－1　 （C）－2　 （D）－3

提示：先化简，再取特殊值。

239、下列命题中正确的是（　）。

  （A）α、β是第一象限角，且α>β，则sinα<sinβ

  （B）△ABC中，tgA＝tgB是A＝B的充分但不必要条件

  （C）函数y＝tg2x的周期为

  （D）函数y＝lg()是奇函数

  提示：全面考察三角函数的各种情况。

240、如果θ∈(, π)，那么复数(1＋i)(cosθ－isinθ)的三角形式是（　）。

  （A）[cos(－θ)＋isin(－θ)]

（B）[cos(2π－θ)＋isin(2π－θ)]

  （C）[cos(＋θ)＋isin(＋θ)]　  

（D）[cos(＋θ)＋isin(＋θ)]

  提示：强调等值、标准。

241、设(1－3x)⁸＝ a₀＋a₁x＋a₂x²＋……＋a₈x⁸，那么a₀＋a₁＋a₂＋……＋a₈的值是（　）。

  （A）1　　 （B）2⁸　　 （C）3⁸　　 （D）4⁸

  提示：取x = -1。

242、设(＋i)ⁿ是纯虚数，则n的可能值是（　）。

  （A）15　　 （B）16　　 （C）17　　 （D）18

  提示：化成复数的三角形式。

243、能使点P(m, n)与点Q(n＋1, m－1)成轴对称的位置关系的对称轴的方程是（ ）。

（A）　　 x＋y＋1＝0 　　　（B）x＋y－1＝0

（B）　　 （C）x－y－1＝0 （D）x－y＋1＝0

  提示：垂直、中点代入验证。

244、项数为2m的等比数列，中间两项是方程x²＋px＋q＝0的两根，那么这个数列的所有项的积为（　）。

  （A）－mp　（B）q^m　（C）pq　（D）不同于以上的答案

  提示：等比数列的性质。

245、已知直线a, b，平面α, β, γ，以下四个条件中，①α⊥γ, β⊥γ；② α内有不共线的三点到β的距离相等；③ aα,bα, a//β, b//β；④ a, b是异面直线，且aα, a//β, bβ, b//α。能推出α//β的是（　）。

  （A）④　 （B）②和③　 （C）②　 （D）①和②

  提示：线面垂直与平行的判定及性质。

246、8次射击命中3次，且恰有2次连续命中的情况共有（　）。

  （A）15种　 （B）30种　 （C）48种　 （D）60种

  提示：组合与排列。

247、函数f (x)＝在区间(0, 1)上是减函数，p＝f (), q＝f (tgθ＋ctgθ), r＝f () (θ为锐角)，则（　）。

  （A）p<q<r　 （B）r<p<q　 （C）q<p<r　 （D）r<q<p

　提示：先确定的范围，再比较、 tgθ＋ctgθ、的大小。

248、函数y＝cos2x＋sin(＋x)是（　）。

  （A）仅有最小值的奇函数　　（B）仅有最大值的偶函数

  （C）有最大值、最小值的偶函数（D）既不是奇函数，也不是偶函数

提示：先配方、再求值。

249、设满足下列条件的函数f (x)的集合为M，当x₁≤1， x₂≤1时，f (x₁)－f (x₂)≤4x₁－x₂, 若有函数g(x)＝x²＋2x－1，则函数g(x)与集合M的关系是（　）。

  （A）g(x)M　 　 （B）g(x)∈M　

（C）g(x)M　 　 （D）不能确定

　提示：当x₁≤1，x₂≤1时，g(x₁)-g(x₂) ≤4x₁－x₂， g(x)是元素。

250、当x∈(1, 2)时，不等式x－1<log_ax恒成立，则a的取值范围是（　）。

  （A）(0, 1)　 （B）(1, 2)　 （C）(1, 2)　 （D）(2, ＋∞)

　提示：利用函数图象，进行分析。

251、已知函数f (x)＝2^x， f ^-1(x)是f (x)的反函数，那么f ^-1(4－x²)的单调递减区间是（　）。

  （A）[0, ＋∞]　 　　 （B）(－∞, 0)　

（C）[0, 2]　 　　　　（D）(－2, 0)

提示：根据复合函数的增减性加以判断。

 252、以下四个命题：① PA、PB是平面α的两条相等的斜线段，则它们在平面α内的射影必相等；② 平面α内的两条直线l₁、l₂，若l₁、l₂均与平面β平行，则α//β；③ 若平面α内有无数个点到平面β的距离相等，则α//β；④ α、β为两相交平面，且α不垂直于β，α内有一定直线a，则在平面β内有无数条直线与a垂直。其中正确命题的个数是（ ）。

  （A）1个　 （B）2个　 （C）3个　 （D）4个

提示：利用垂直、平行等知识，逐个分析。

 253、已知，则x＋y的取值范围是（ ）。

  （A）(0, 1)　 （B）[2, ＋∞]　 （C）(0, 4)　 （D）[4, ＋∞]

提示：x+y=xy 不小于xy的算术平方根的两倍。

254、若函数f (x)的定义域为－≤x≤，则f (sinx)的定义域是（　）。

  （A）[－, ]　

 （B）[, ]　

 （C）[2kπ＋, 2kπ＋],k∈Z

 （D）[2kπ－, 2kπ＋]∪[2kπ＋, 2kπ＋],k∈Z

  提示：借助函数图象，解三角不等式。

 

　　　　　　　　　　  于2003．3月