高考数学综合训练（1）
第I卷（选择题 共60分）
一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）
1．设集合M={xx-m≤0}，
，若M∩N=φ，则实数m的取值范围是（ ）
A．m≥-1 B．m>-1 C．m≤-1 D．m<-1
2．若直线l过点（3，0）且与双曲线
只有一个公共点，则这样的直线有（
）
A．1条 B．2条 C．3条 D．4条
3．对总数为N的一批零件抽取一个容量为30的样本，若每个零件被抽取的概率为0.25，则N等于（ ）
A．150 B．200 C．120 D．100
4．A、B、C、D、E五种不同的商品要在货架上排成一排，其中A、B两种商品必须排在一起，而C、D两种商品不能排在一起，则不同的排法共有（ ）
A．12种子 B．20种 C．24种 D．48种
5．设函数
，则f(x)的反函数
的图象是（ ）
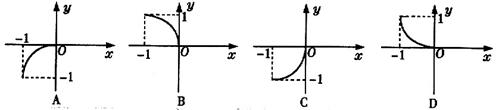
6．买4枝郁金香和5枝丁香的金额和小于22元，而买6枝郁金香和3枝丁香的金额之和大于24元，那么买2支郁金香和买3枝丁香的金额比较，其结果是（ ）
A．2枝郁金香贵 B．3枝丁香贵
C．相同 D．不能确定
7．若不等式
对x∈R恒成立，则关于t的不等式
的解为（ ）
A．1<t<2 B．-2<t<1 C．-2<t<2 D．-3<t<2
8．在△ABC中，
，且
，则△ABC的形状是（ ）
A．直角三角形 B．钝角三角形
C．等腰三角形 D．等边三角形
9．曲线
在
处的切线平行于直线y=4x-1，则坐标为（ ）
A．（1，0） B．（2，8）
C．（1，0）或（-1，-4） D．（2，8）或（-1，-4）
10．已知全集I=R，
，则
A等于（ ）
A．（-∞，1） B．[0，1）
C．（-∞，0）∪[1，+∞） D．[1，2]
11．已知正方体的八个顶点中，有四个点恰好为正四面体的顶点，则该正四面体的体积与正方体的体积之比为（ ）
A．
B．2：3 C．1：2 D．1：3
12．若数列
的n项的和
，则“c=-1”是“数列为等比数列”的（ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分又不必要条件
第II卷（非选择题 共90分）
二、填空题（本大题共4个小题，每小题4分，共16分，把答案填在题中横线上）
13．圆锥的母线长为3，侧面展开所成的扇形的中心角为
，则圆锥的侧面积为_______________。
14．已知
，直线l过点A（3，-1），且与向量
垂直，则直线l的一般式方程为_______________。
15．点A的坐标为（3，1），若P是抛物线
上的一动点，F是抛物线的焦点，则PA+PF的最小值为_______________。
16．f(x)是定义在R上的奇函数，它的最小正周期T，则
的值为_______________。
三、解答题（本大题共6个小题，共74分，解答应写出必要文字说明、证明过程或演算步骤）
17．（本小题满分12分）
若f(x)在定义域（-1，1）内可导，且f′(x)<0；又当a，b∈（-1，1）且a+b=0时，f(a)+f(b)=0，解不等式
。
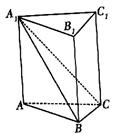
18．（本小题满分12分）
直三棱柱
的侧棱
，底面△ABC中，∠C=90°，AC=BC=1。
（1）求证：
；
（2）求点
到
的距离；
（3）求AB与所成角的正弦值。
19．（本小题满分12分）
设两向量
满足
，的夹角为60°，若向量
与向量
的夹角为钝角，求实数t的取值范围。
20．（本小题满分12分）
某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律：每生产产品x（百台），其总成本为G（x）（万元），其中固定成本为2万元，并且每生产1百台的生产成本为1万元（总成本=固定成本+生产成本）；销售收入R（x）（万元）满足：
，
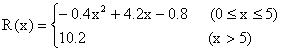假定该产品产销平衡，那么根据上述统计规律。
（1）要使工厂有赢利，产量x应控制在什么范围？
（2）工厂生产多少台产品时，可使赢利最多？
（3）求赢利最多时每台产品的售价。
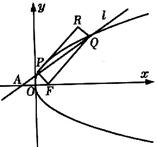
21．（本小题满分12分）
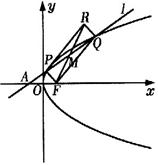
如图，过点A（-1，0），斜率为k的直线l与抛物线C：交于P、Q两点。
（1）若曲线C的焦点F与P，Q，R三点按如图顺序构成平行四边形PFQR，求点R的轨迹方程；
（2）设P，Q两点只在第一象限运动，（0，8）点与线段PQ中点的连线交x轴于点N，当点N在A点右侧时，求k的取值范围。
22．（本小题满分14分）
数列各项均为正数，
为其前n项的和。对于
，总有
成等差数列。
（1）求数列的通项
；
（2）设数列
的前n项和为
，数列
的前n项和为
，求证：当n≥2，时，
；
（3）若函数
的定义域为R，并且
（），求证：p+q>1。
参考答案
一、选择题
1．D 
，
而
∴
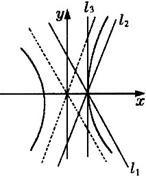
2．C 
，a=3，b=2，∴点（3，0）即顶点，如图所示，
，
，
三条.（
轴，，平行于渐近线）
3．C 由题
∴N=120
4．C 将A、B捆绑在一起，再使用插入法
，
5．B 
值域为原函数的定义域，即[0，1]，排除A、C取
，
，∴点
在
上，则选B
6．A 曲线性规划知识易得.
7． A 
恒成立，则
∴ 0<a<1
∴
∴
8．D 
∴
，而
∴
∴A=B
9．C 
∴x=±1 ∴
为（1，0）或（-1，-4）
10．C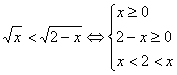 
∴
11．D 如图ABCD即为正四面体，棱长为正方体面对角线，根据体积公式易得
12．C 若
，
，易证
为等比；
若，等比，
∴ 
∴.
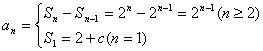
二、填空题
13．
∴r=1 ∴
14．
向量
∴
∴
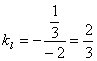
15．4 如右图
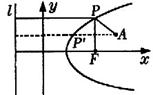
准线为l，
到l的距离.
∴ 
到l的距离=4
16．0 可比照
. 
令
∴
即
∴
三、解答题
17．解：∵f(x)在（-1，1）内可导，且
∴
在（-1，1）上为减函数
又当
，a+b=0时，
∴
，即
，即
∴f(x)在
上为奇函数
∴ 
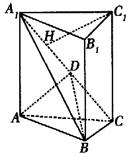
18．解：（1）∵
，
，
。
∴
。
（2）∵
，
∴点到
到平面
的距离即为点
到平面的距离。
∵
，又BC⊥AC，
∴
。
作
，垂足
。
∵。
∴
，即
∴
。
则
的长度即为点到平面的距离，
而在
中，
，
，
∴
即为所求点到平面的距离。
（3）在平面
内作
，垂足
。
由知BC⊥AO，即AO⊥BC，
∴
.连BO，
则BO为AB在平面内的射影。
∴∠ABO为AB与平面所成的角（设为θ）。
而
，
，
∴
.
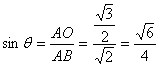19．解：
，
，
∴
∴
∴
，
设
∴
∴当
时，
与
的夹角为π
∴
20．依题意，
.设利润函数为f(x)，则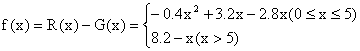
（1）要使工厂有赢利，即解不等式
，当
时，
解不等式
。
即
.
∴1<x<7，∴
。
当x>5时，解不等式
，
得
。 ∴
。
综上，要使工厂赢利，x应满足1<x<8.2，
即产品应控制在大于100台，小于820台的范围内。
（2）时，
，故当x=4时，f(x)有最大值3.6.（8分）而当x>5时，
所以，当工厂生产400台产品时，赢利最多.
（3）即求x=4时的每台产品的售价.此时售价为
（万元/百台）=240元/台.
21．解：（1）由已知
，
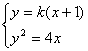消x得
∵直线l交C于两点P、Q，
∴
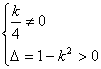
得
或
。
设
，
，M是PQ中点，
∵
，
∴M点纵坐标
，将其代入l方程，得
，
∵PFQR是平行四边形，
∴R、F中点也是M，而F（1，0）
∴
，
消k得
。
又∵
，
∴
，
∴点R的轨迹方程为
（2）∵P、Q在第一象限
∴
∴
，
结合（1）得
① （0，8）点与PQ中点所在直线方程为
令
，得N点横坐标
∵N在点A右侧 ∴令
，得
。
解之得
或
②
综合①②，k的取值范围是
。
22．（1）解：由已知
时，
总成立。
∴
（n≥2）两式作差，
得
∴ 
，
∵
、
均为正数
∴
（
）。
∴是公差为1的等差数列。
又n=1时，
，得
，∴
。
（2）证明：①当n=2时，
，
。
∴
时，等式成立。
②假设当n=k时，等式成立，即
，
那么当
时， 
。
∴当
时，等式也成立。综合①②，等式成立。
（3）证明：如果q=0，则
不是0，∴
。
∵定义域为全体实数。
∴
恒成立即
恒成立。
由于时，
的值域为
，∴
，又当
时，
。
，∴
。
∵
∴
∴
∴
。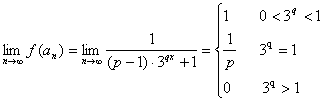