高考模拟试题数学试卷
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至3页,第Ⅱ卷4至9页,共150分,考试用时120分钟.
第Ⅰ卷(选择题 共60分)
注意事项:
1. 答题前,考生在答题卡上务必用黑色签字笔将自己的姓名、班别、学号填写清楚。
2. 每小题选出答案后,用铅笔马答题卡上对应题目的答案标号涂黑,如需改动,用橡
皮擦干净后,再选涂其它答案,不能答在试题卷上。
3.考试结束,监考人将本试卷和答题卡一并收回。
参考公式:
三角函数的和差化积公式
![]()
![]()
![]()
![]()
正棱台、圆台的侧面积公式
![]()
其中c′、c 分别表示上、下底面周长,
l表示斜高或母线长
台体的体积公式
![]()
其中S′、S分别表示上、下底面积,h表示高
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知复数z=l-i ,则z4=( )
(A)2 (B)4 (C)8 (D)16
2.直线![]() 与圆x2+y2=1在第一象限内有两个不同的交点,则m的取值范围是( )
与圆x2+y2=1在第一象限内有两个不同的交点,则m的取值范围是( )
(A)![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
3.集合M={a,b,c}, N={-1,0,1},映射f: M →N 满足f(a)+f(b)+f(c)=0, 那么 映射 f: M →N的个数是( )
(A)4 (B)5 (C)6 (D)7
4.若圆的极坐标方程为![]() 则圆心的极坐标是( )
则圆心的极坐标是( )
(A) (2,![]() )
(B) (2,
)
(B) (2,![]() )
(C) (1,
)
(C) (1,![]() ) (D)
(1,
) (D)
(1,![]() )
)
5.已知![]() ,则
,则![]() 的值为(
)
的值为(
)
(A)1 (B)-1 (C)0 (D)不存在
6.圆锥轴截面的顶角为![]() ,过顶点的截面三角形的最大面积为2,则圆锥的侧面积及体积分别为( )
,过顶点的截面三角形的最大面积为2,则圆锥的侧面积及体积分别为( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
7. 五个身高均不相同的学生排成一排俣影留念,高个子站中间,从中间到左边和从中间到右边均一个比一个矮,则这样的排法共有 ( )
(A)6种 (B)8种 (C)12种 (D)16种
8.要得到函数![]() 的图象,只要将函数
的图象,只要将函数![]() 的图象( )
的图象( )
(A)向左平移![]() 个单位
(B) 向右平移
个单位
(B) 向右平移![]() 个单位
个单位
(C)向左平移![]() 个单位 (D) 向右平移
个单位 (D) 向右平移![]() 个单位
个单位
9.函数![]() 在(-1,1)上存在x0,使
在(-1,1)上存在x0,使![]() ,则a的取值范围是( )
,则a的取值范围是( )
(A)![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
 10.已知又曲线
10.已知又曲线![]() 的焦点是
的焦点是![]() ,而点P在双曲线C上,PF1,F1F2,PF2成等比数列,且PF2<4,则b= ( )
,而点P在双曲线C上,PF1,F1F2,PF2成等比数列,且PF2<4,则b= ( )
(A)1 (B)2 (C)3 (D)4
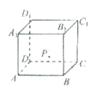
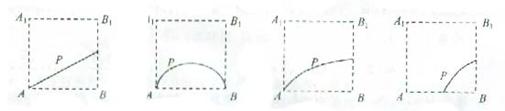 11.如图示,在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到直线A1B1与直线BC的距离相等,则动点P所在曲线的形状为 ( )
11.如图示,在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到直线A1B1与直线BC的距离相等,则动点P所在曲线的形状为 ( )
(A) (B) (C) (D)
12.若x![]() R, n
R, n![]() N,定义:M
N,定义:M![]() =x(x+1)(x+2)…(x+n-1)
=x(x+1)(x+2)…(x+n-1)
如![]() ,则函数
,则函数![]() 的奇偶性为 (
)
的奇偶性为 (
)
(A)是偶函数而不是奇函数 (B) 是奇函数而不是偶函数
(C) 既是偶函数又是奇函数 (D) 既不是偶函数也不是奇函数
第Ⅱ卷(非选择题 共60分)
注意事项:第Ⅱ卷共6页,用钢笔或圆珠笔直接答在试题卷中
二、填空题:本大题共4个小题,每小题4分,共16分,把答案填在题中横线上
13. 函数![]() 的反函数是: .
的反函数是: .
14. 若![]() 展开式中x的一次项是第6项,则n的值是 .
展开式中x的一次项是第6项,则n的值是 .
15. 我国于2003年10月15日成功发射载入“神舟五号”宇宙飞船,杨利伟随飞船绕地球习行了14圈,飞船飞行的轨道是以地球的中心为一个焦点的椭圆,近地点距地面200千米,远地点距地面350千米,若地球半径为6371千米,则此椭圆的离心率为 .
16. 已知直线m![]() 平面a,直线n
平面a,直线n![]() 平面
平面![]() ,给出下列命题:
,给出下列命题:
①a∥![]()
![]() m
m![]() n; ②a
n; ②a![]()
![]()
![]() m∥n; ③m∥n
m∥n; ③m∥n![]() a
a![]()
![]() ; ④m
; ④m![]() n
n![]() a∥
a∥![]() ;
;
其中正确命题的序号是 .(要注:把正确命题的序号都填上)
三、解答题: 本大题共6小题,共74分,解答应写出文说明、证明过程或演算步骤.
17. (本小题满分12分)已知复数![]() A、B、C是△ABC的内角
A、B、C是△ABC的内角
(1)求A: (2)求sinB+sinC的取值范围
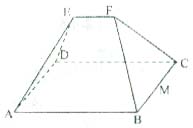
18. (本小题满分12分)如图所示的一个几何体中,底面ABCD是矩形,AB=9,BC=8,EF∥平面ABCD,且EF=3,EA=ED=FB=FC=13.
(1) 求异面直线AE与CF所成的角;
(2) 求二面角F-BC-D的大小;
19. (本小题满分12分)在等差数列![]() 中,首项a1=1,数列
中,首项a1=1,数列![]() 满足
满足![]() ,且
,且![]() .
.
(1) 求数列![]() 的通项公式:
的通项公式:
(2)求证:![]() .
.
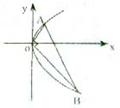
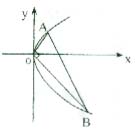 20.(本小题满分12分)已知Rt△OAB的三顶点O、A、B都在抛物线
20.(本小题满分12分)已知Rt△OAB的三顶点O、A、B都在抛物线![]() 上(如图),OA
上(如图),OA![]() OB.
OB.
(1) 若直线OA的斜率为2,AB=![]() ,求抛物线C的方程;
,求抛物线C的方程;
(2) 若A(x1,y1),B(x2,y2),求证:x1x2与y1y2均为定值.
21.(本小题满分12分)
随着我国加入WTO,某企业决定从甲、乙两种畅销产品中选择一种进行投资生产,打入国际市场已知投资生产这两种产品的有关数据如下表(单位:万美元)
|
| 年固定成本 | 每件产品成本 | 每件产品 销售价 | 每年最多生产的件数 |
| 甲产品 | 30 | a | 10 | 200 |
| 乙产品 | 50 | 8 | 18 | 120 |
其中年固定成本与生产的件数无关,a为常数,且4≤a≤8另外,年销售x件乙产品时需上交0.05x2万美元的特别关税.
(1)写出该厂分别投资生产甲、乙两种产品的年利润y1,y2与生产相应产品的件数![]() 之间的函数关系式;
之间的函数关系式;
(2)分别求出投资生产这两种产品的最大年利润;
(3) 如何决定投资可获最大年利润?
22. (本小题满分14分)已知![]() 是定义在(-
是定义在(-![]() ,+
,+![]() )上的偶函数,且满足
)上的偶函数,且满足![]() ,当
,当![]() 时,
时, ![]() =-2(x-3)2+4.
=-2(x-3)2+4.
(1)
当![]() 时,求
时,求![]() 的解析式;
的解析式;
(2)
若矩形ABCD的两个顶点A、B在x轴上,C、D在函数y=![]() (0≤x≤2)的图象上,求矩形ABCD面积的最大值.
(0≤x≤2)的图象上,求矩形ABCD面积的最大值.
高考模拟试题数学参考答案
一、选择题:1.B 2.C 3.D 4.D 5.A 6.B 7.A 8.D 9.C 10.A 12.C 12.B
二、填空题:13. ![]() 14. 8 15.
14. 8 15. ![]() 16. ①③
16. ①③
三、解答题:
17.
解:(1)∵![]() ……(2分)
……(2分)
∴![]() ……(4分)
……(4分)
(2)∵![]() ……(6分)
……(6分)
![]() ……(7分)
……(7分)
又∵0<C<![]() ,∴-
,∴-![]() <
<![]() -C<
-C<![]() ……(9分)
……(9分)
∴![]() ……(11分)
……(11分)
∴sinB +
sinC的取值范围是:(![]() ,
,![]() ……(12′)
……(12′)
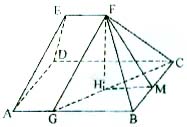 18. 解: 在平面ABEF内,过F作FG∥AE交AB于点G,
18. 解: 在平面ABEF内,过F作FG∥AE交AB于点G,
则∠GFC为异面直线AE与CF所成的角, …… (2分)
连结GC, ∵EF=3,AB=9, ∴GB=6 又∵四边形ABCD为矩形,且BC=8,
在Rt△GBC中,GC=![]() ;又在△FGC中,
;又在△FGC中,
FG=FC=13, GC=10. …………(4分)
∴![]()
∴异面直线AE与CF所成的角为![]()
![]() 。 ……(6分)
。 ……(6分)
(2)∵FB=FG=FC, ∴F在平面ABCD上的射影H是Rt△GBC的外心,即H是GC的中点,取BC的中点M,连结FM、HM. … … … … (7分)
∵FB=FC=13, ∴FM![]() BC. ①… …
… (8分)
BC. ①… …
… (8分)
且FM=![]() .
.
又∵HM∥AB,HM=![]() GB=3,
GB=3,
∴HM![]() BC.
②… … … … (9分)
BC.
②… … … … (9分)
由①、②查得![]() FMH是二面角F-BC-D的平面角.… … … (10分)
FMH是二面角F-BC-D的平面角.… … … (10分)
在Rt△FHM中,![]()
∴二面角F-BC-D的大小为![]()
![]() … …(12分)
… …(12分)
19. 解:(1)设等差数列![]() 的公差为d.
的公差为d.
∵![]()
∴![]() … … (3分)
… … (3分)
由![]() 解得
解得![]() …… (5分)
…… (5分)
∴![]() ……(6分)
……(6分)
(2)由(1)得, ![]()
设![]()
则![]()
两式相减得: ![]() …… (9分)
…… (9分)
∴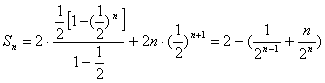 …… (11分)
…… (11分)
∵![]() >0 ∴
>0 ∴![]() <2 …… (12分)
<2 …… (12分)
 20. 解:(1)由
20. 解:(1)由![]() …… (1分)
…… (1分)
同理可得B (8P,-4P) ……(2分)
由AB=5![]() 得
得
![]() …(3分)
…(3分)![]() …… (4分)
…… (4分)
p>0, ∴p=2. …… (5分) ∴C的方程为![]()
(2) ∵![]()
∴![]() …… (7分)
…… (7分)
又∵OA![]() OB, ∴
OB, ∴![]() …… (9分)
…… (9分)
![]()
![]() =
=![]() ……(11分)
……(11分)
∴![]() …… (12分)
…… (12分)
21. 解:(1) 依题:![]() …… (2分)
…… (2分)
![]() …… (4分)
…… (4分)
(2) ∵![]() ∴
∴![]()
∴![]() …… (6分)
…… (6分)
∵![]()
∴当![]() …… (8分)
…… (8分)
(3)令![]() ,得a=7.6 …… (9分)
,得a=7.6 …… (9分)
∴当4≤a<7.6时,投资甲产品 …… (10分)
当7.6<a≤8时,投资乙产品 …… (11分)
当a=7.6 时,投资甲乙两产品均可 …… (12分)
(由![]() 也可)
也可)
22.解:(1)![]() 是定义在(-
是定义在(-![]() ,+
,+![]() )上的偶函数,且
)上的偶函数,且![]()
当![]() 时,有2≤x+2≤3
时,有2≤x+2≤3
故![]() …… (2分)
…… (2分)
 当
当![]() ,有
,有![]() ,则
,则![]() …… (3分)
…… (3分)
有![]() …… (4分)
…… (4分)
![]() …… (5分)
…… (5分)
∴当![]() 时,
时, ![]() …… (6分)
…… (6分)
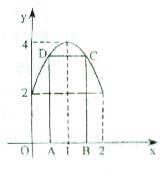
(2)∵矩形两顶点A、B在x轴上,C、D在
![]() (0≤x≤2)的图象上,如图所示,
(0≤x≤2)的图象上,如图所示,
设AB=2t, ![]() ,则A(1-t,0),B(1+t.0)
,则A(1-t,0),B(1+t.0)
则BC=AD=f(1+t)=-2t2+4
∴![]() …… (9分)
…… (9分)
![]()
∵![]()
∴![]() ≤8·
≤8·![]() …… (12分)
…… (12分)
当且仅当![]() ,即
,即![]() ,即当点A的横坐标
,即当点A的横坐标![]() 时取等号 … (13分)
时取等号 … (13分)
∴![]()
∴矩形ABCD面积的最大值是![]() (14分)
(14分)
